名校
解题方法
1 . 已知椭圆 的右焦点为
的右焦点为 ,上顶点为
,上顶点为 ,
, ,离心率为
,离心率为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)若直线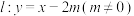 与椭圆
与椭圆 相交于
相交于 两点,且点
两点,且点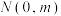 ,当
,当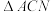 的面积最大时,求直线
的面积最大时,求直线 的方程.
的方程.
 的右焦点为
的右焦点为 ,上顶点为
,上顶点为 ,
, ,离心率为
,离心率为 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)若直线
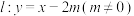 与椭圆
与椭圆 相交于
相交于 两点,且点
两点,且点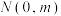 ,当
,当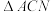 的面积最大时,求直线
的面积最大时,求直线 的方程.
的方程.
您最近一年使用:0次
2023-07-26更新
|
1532次组卷
|
14卷引用:河北省衡水市深州中学2023-2024学年高二下学期期末考试数学试题
河北省衡水市深州中学2023-2024学年高二下学期期末考试数学试题广西壮族自治区河池市2022-2023学年高二下学期期末教学质量检测数学试题广东省湛江市第一中学2024届高三上学期开学考试数学试题广东省潮州市潮安区凤塘中学2024届高三上学期统测(一)数学试题(已下线)高二上学期期中数学试卷(基础篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第一册)(已下线)第三章 圆锥曲线的方程 章末测试(基础)-2023-2024学年高二数学《一隅三反》系列(人教A版2019选择性必修第一册)(已下线)第五节 椭圆 第二课时 直线与椭圆的位置关系 B素养提升卷广东省郁南县连滩中学2024届高三上学期9月月考数学试题(已下线)考点14 直线与圆锥曲线相交问题 2024届高考数学考点总动员【练】江苏省扬州市宝应县2023-2024学年高二上学期期中数学试题广东省汕尾市陆河县陆河外国语学校2023-2024学年高三上学期11月期中数学试题浙江省诸暨中学暨阳分校2023-2024学年高二上学期期中考试数学试题广东省惠州市博罗县博师高级中学2024届高三上学期9月月考数学试题安徽省合肥市庐江县2023-2024学年高二上学期第二次集体练习数学试题
名校
解题方法
2 . 已知过点 的直线与椭圆
的直线与椭圆 交于
交于 、
、 两点,则弦长
两点,则弦长 可能是( )
可能是( )
| A.1 | B. | C. | D.3 |
您最近一年使用:0次
2023-09-21更新
|
1431次组卷
|
8卷引用:2023届高三上学期一轮复习联考(五)数学试题(新高考卷)
2023届高三上学期一轮复习联考(五)数学试题(新高考卷)山东省聊城市聊城一中东校等2校2023届高三上学期期末数学试题(已下线)考点巩固卷20 椭圆方程及其性质(十大考点)江西省宜春市万载县赣西外国语学校2023-2024学年高二上学期期中数学试题(A卷)江西省赣西外国语学校2023-2024学年高二上学期期中考试数学B卷山东省济宁市泗水县2023-2024学年高二上学期期中数学试题(已下线)专题23 椭圆的简单几何性质10种常见考法归类(2)(已下线)专题10 椭圆的几何性质8种常见考法归类(2)
名校
解题方法
3 . 已知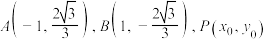 为椭圆
为椭圆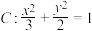 上不同的三点,直线
上不同的三点,直线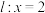 ,直线
,直线 交
交 于点
于点 ,直线
,直线 交
交 于点
于点 ,若
,若 ,则
,则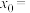 ( )
( )
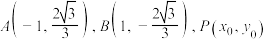 为椭圆
为椭圆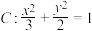 上不同的三点,直线
上不同的三点,直线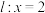 ,直线
,直线 交
交 于点
于点 ,直线
,直线 交
交 于点
于点 ,若
,若 ,则
,则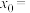 ( )
( )| A.0 | B.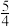 | C.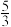 | D. |
您最近一年使用:0次
2022-11-24更新
|
1726次组卷
|
10卷引用:河北省邯郸市魏县2022-2023学年高二上学期期末考试数学试题
河北省邯郸市魏县2022-2023学年高二上学期期末考试数学试题浙江省杭州市源清中学2022-2023学年高二上学期期末数学试题浙江省台金六校2022-2023学年高二上学期期中联考数学试题福建省三校联考2022-2023学年高二上学期期中考试数学试题江苏省扬州中学2022-2023学年高二上学期12月月考数学试题辽宁省沈阳市东北育才学校2023届高三高考适应性测试(二)数学试题(已下线)第五节 椭圆 第二课时 直线与椭圆的位置关系 B素养提升卷重庆市第八中学校2023-2024学年高二上学期定时检测(四)数学试题(已下线)专题12 椭圆-2浙江省宁波市鄞州中学2023-2024学年高二上学期9月月考数学试题
4 . 已知平面内两定点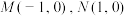 ,动点P满足
,动点P满足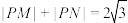 .
.
(1)求动点P的轨迹C的方程;
(2)若直线 与曲线C交于不同的两点A、B,求
与曲线C交于不同的两点A、B,求 .
.
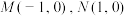 ,动点P满足
,动点P满足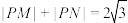 .
.(1)求动点P的轨迹C的方程;
(2)若直线
 与曲线C交于不同的两点A、B,求
与曲线C交于不同的两点A、B,求 .
.
您最近一年使用:0次
2024-01-14更新
|
850次组卷
|
6卷引用:河北省石家庄市第二十二中学2023-2024学年高二上学期期末数学模拟试卷
河北省石家庄市第二十二中学2023-2024学年高二上学期期末数学模拟试卷广西贵港高中2020-2021学年高二上学期理科期中教学质量监测试题(已下线)【新教材精创】3.1.2+椭圆的简单几何性质(2)-B提高练-人教A版高中数学选择性必修第一册(已下线)专题3.1 椭圆-《讲亮点》2021-2022学年高二数学新教材同步配套讲练(苏教版2019选择性必修第一册)河南省兰考县第二高级中学2021-2022学年高二上学期第三次考试数学试题 上海市南洋模范中学2023-2024学年高二下学期4月段考数学试卷
5 . 椭圆 的两焦点为
的两焦点为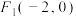 ,
,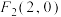 ,且椭圆过点
,且椭圆过点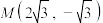 .
.
(1)求椭圆的方程;
(2) 是坐标原点,
是坐标原点, 是椭圆上两点,
是椭圆上两点, 是平行四边形,求以
是平行四边形,求以 为直径的圆的方程.
为直径的圆的方程.
 的两焦点为
的两焦点为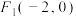 ,
,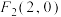 ,且椭圆过点
,且椭圆过点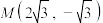 .
.(1)求椭圆的方程;
(2)
 是坐标原点,
是坐标原点, 是椭圆上两点,
是椭圆上两点, 是平行四边形,求以
是平行四边形,求以 为直径的圆的方程.
为直径的圆的方程.
您最近一年使用:0次
2023-07-09更新
|
677次组卷
|
5卷引用:河北省邢台市2022-2023学年高二下学期期末数学试题
河北省邢台市2022-2023学年高二下学期期末数学试题(已下线)第20讲 椭圆的简单几何性质10种常见考法归类(3)(已下线)模块一 专题4 圆锥曲线 期末终极研习室(2023-2024学年第一学期)高二人教A版(已下线)专题3.1 椭圆(5个考点十四大题型)(4)福建省泉州市安溪第一中学2023-2024学年高二下学期6月份质量检测数学试题
名校
解题方法
6 . 已知椭圆 过点
过点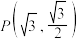 ,离心率为
,离心率为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)若 为椭圆
为椭圆 的左顶点,直线
的左顶点,直线 过右焦点
过右焦点 与椭圆
与椭圆 交于
交于 ,
, 两点(
两点( ,
, 与
与 不重合),
不重合), 不与
不与 轴垂直,若
轴垂直,若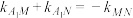 ,求
,求 .
.
 过点
过点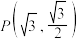 ,离心率为
,离心率为 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)若
 为椭圆
为椭圆 的左顶点,直线
的左顶点,直线 过右焦点
过右焦点 与椭圆
与椭圆 交于
交于 ,
, 两点(
两点( ,
, 与
与 不重合),
不重合), 不与
不与 轴垂直,若
轴垂直,若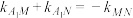 ,求
,求 .
.
您最近一年使用:0次
2021-08-08更新
|
1587次组卷
|
8卷引用:河北省石家庄一中2023-2024学年高二上学期期末数学试题
河北省石家庄一中2023-2024学年高二上学期期末数学试题江西省重点中学盟校2021届高三第一次联考数学(文)试题广东省江门市蓬江区培英高中2021届高三5月份数学冲刺试题(已下线)专题02 圆锥曲线弦长问题-【解题思路培养】2022年高考数学一轮复习解答题拿分秘籍(全国通用版)(已下线)试卷11(第1章-4.1数列)-2021-2022学年高二数学易错题、精典题滚动训练(苏教版2019选择性必修第一册)(已下线)专题20 椭圆、抛物线(解答题)-备战2022年高考数学(理)母题题源解密(全国甲卷)(已下线)专题21 椭圆、抛物线(解答题)-备战2022年高考数学(文)母题题源解密(全国甲卷)福建省晋江二中、鹏峰中学、广海中学、泉港五中2023届高三上学期12月联考数学试题
7 . 已知椭圆C的右焦点与抛物线E: 的焦点F重合,且椭圆C的离心率为
的焦点F重合,且椭圆C的离心率为 .
.
(1)求椭圆C的标准方程.
(2)过点F的直线l交椭圆C于M,N两点,交抛物线E于P,Q两点,是否存在实数 ,使得
,使得 为定值?若存在,求出这个定值和λ的值;若不存在,说明理由.
为定值?若存在,求出这个定值和λ的值;若不存在,说明理由.
 的焦点F重合,且椭圆C的离心率为
的焦点F重合,且椭圆C的离心率为 .
.(1)求椭圆C的标准方程.
(2)过点F的直线l交椭圆C于M,N两点,交抛物线E于P,Q两点,是否存在实数
 ,使得
,使得 为定值?若存在,求出这个定值和λ的值;若不存在,说明理由.
为定值?若存在,求出这个定值和λ的值;若不存在,说明理由.
您最近一年使用:0次
2023-01-03更新
|
511次组卷
|
3卷引用:河北省部分学校2023届高三上学期期末数学试题
河北省部分学校2023届高三上学期期末数学试题吉林省松原市前郭尔罗斯蒙古族自治县第五中学2022-2023学年高三上学期期末考试数学试题(已下线)重难点突破06 弦长问题及长度和、差、商、积问题(七大题型)-2
名校
解题方法
8 . 设椭圆 的左,右焦点分别为
的左,右焦点分别为 ,其离心率为
,其离心率为 ,且点
,且点 在C上.
在C上.
(1)求C的方程;
(2)O为坐标原点,P为C上任意一点.若M为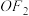 的中点,过M且平行于
的中点,过M且平行于 的直线l交椭圆C于A,B两点,是否存在实数
的直线l交椭圆C于A,B两点,是否存在实数 ,使得
,使得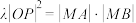 ?若存在,求
?若存在,求 值;若不存在,说明理由.
值;若不存在,说明理由.
 的左,右焦点分别为
的左,右焦点分别为 ,其离心率为
,其离心率为 ,且点
,且点 在C上.
在C上.(1)求C的方程;
(2)O为坐标原点,P为C上任意一点.若M为
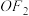 的中点,过M且平行于
的中点,过M且平行于 的直线l交椭圆C于A,B两点,是否存在实数
的直线l交椭圆C于A,B两点,是否存在实数 ,使得
,使得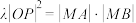 ?若存在,求
?若存在,求 值;若不存在,说明理由.
值;若不存在,说明理由.
您最近一年使用:0次
2022-02-21更新
|
845次组卷
|
18卷引用:河北省唐山市2019-2020学年高二上学期期末数学试题
河北省唐山市2019-2020学年高二上学期期末数学试题河北省秦皇岛市抚宁区第一中学2019-2020学年高二上学期期末数学试题宁夏石嘴山市第三中学2019-2020学年高二上学期期末考试数学(理)试题海南省海南枫叶国际学校2019-2020学年高二上学期期末考试数学试题广西桂林市2021-2022学年高二上学期期末考试数学(理)试题贵州省贵阳市第一中学2020届高三上学期第三次月考数学(文)试题2020届江西省赣州市赣县三中高三1月考前适应性考试数学(理)试题(已下线)专题05 圆锥曲线中的证明问题、探究性问题(第五篇)-2020高考数学压轴题命题区间探究与突破四川省宜宾市叙州区第二中学校2020届高三第一次高考适应性考试数学(理)试题四川省宜宾市叙州区第二中学校2020届高三第一次高考适应性考试数学(文)试题(已下线)专题19 圆锥曲线综合-2020年高考数学(理)母题题源解密(全国Ⅱ专版)(已下线)专题19 圆锥曲线综合-2020年高考数学(文)母题题源解密(全国Ⅱ专版)西藏山南市第二高级中学2020届高三第三次模拟考试数学(文)试题西藏山南市第二高级中学2020届高三第三次模拟考试数学(理)试题(已下线)解密18 椭圆 (讲义)-【高频考点解密】2022年高考数学二轮复习讲义+分层训练(全国通用)(已下线)专题29 弦长问题及长度和、差、商、积问题-2第三章 圆锥曲线的方程单元测试(基础版)-【新教材优创】突破满分数学之2022-2023学年高二数学重难点突破+课时训练 (人教A版2019选择性必修第一册)江西省南昌市铁路第一中学2022-2023学年高二下学期3月月考数学试题
解题方法
9 . 设椭圆E: (
( )的左、右焦点分别为
)的左、右焦点分别为 ,
,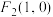 ,点
,点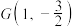 在椭圆E上.
在椭圆E上.
(1)求椭圆E的方程;
(2)设点T在直线 上,过T的两条直线分别交E于A,B两点和P,Q两点,且
上,过T的两条直线分别交E于A,B两点和P,Q两点,且 ,求直线
,求直线 的斜率与直线
的斜率与直线 的斜率之和.
的斜率之和.
 (
( )的左、右焦点分别为
)的左、右焦点分别为 ,
,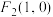 ,点
,点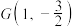 在椭圆E上.
在椭圆E上.(1)求椭圆E的方程;
(2)设点T在直线
 上,过T的两条直线分别交E于A,B两点和P,Q两点,且
上,过T的两条直线分别交E于A,B两点和P,Q两点,且 ,求直线
,求直线 的斜率与直线
的斜率与直线 的斜率之和.
的斜率之和.
您最近一年使用:0次
2022-12-27更新
|
757次组卷
|
4卷引用:河北省保定市2023届高三上学期期末数学试题
河北省保定市2023届高三上学期期末数学试题江苏省南通市2022-2023学年高三上学期12月调研测试数学试题(已下线)北京市海淀区2023届高三上学期期末练习数学试题变式题16-21(已下线)第五篇 向量与几何 专题5 调和点列 微点4 调和点列综合训练
名校
10 . 已知椭圆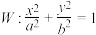 (
( )的左、右焦点分别是
)的左、右焦点分别是 ,
, ,点
,点 为
为 的上顶点,点
的上顶点,点 在
在 上,
上, ,且
,且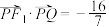 .
.
(1)求 的方程;
的方程;
(2)已知过原点的直线 与椭圆
与椭圆 交于
交于 ,
, 两点,垂直于
两点,垂直于 的直线
的直线 过
过 且与椭圆
且与椭圆 交于
交于 ,
, 两点,若
两点,若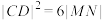 ,求
,求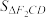 .
.
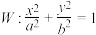 (
( )的左、右焦点分别是
)的左、右焦点分别是 ,
, ,点
,点 为
为 的上顶点,点
的上顶点,点 在
在 上,
上, ,且
,且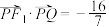 .
.(1)求
 的方程;
的方程;(2)已知过原点的直线
 与椭圆
与椭圆 交于
交于 ,
, 两点,垂直于
两点,垂直于 的直线
的直线 过
过 且与椭圆
且与椭圆 交于
交于 ,
, 两点,若
两点,若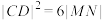 ,求
,求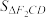 .
.
您最近一年使用:0次
2020-02-09更新
|
1766次组卷
|
20卷引用:河北省邯郸市2019-2020学年高二上学期期末数学试题
河北省邯郸市2019-2020学年高二上学期期末数学试题河北省2019-2020学年高二上学期期末数学试题云南省楚雄州2019-2020学年高二上学期期末数学(理)试题广西壮族自治区来宾市2019-2020学年高二上学期期末数学(理)试题陕西省商洛市2019-2020学年高二上学期期末数学(理)试题贵州省北京师范大学遵义附属学校2020-2021学年高二上学期期末考试数学(理)试题2020届河南省名校联盟高三模拟仿真考试数学(理科)试题2020届河南省名校联盟高三模拟仿真考试数学(文科)试题陕西省汉中市部分学校2019-2020学年高三下学期3月线上模拟调研测试数学(理)试题(已下线)理科数学-2020年高考押题预测卷03(新课标Ⅰ卷)《2020年高考押题预测卷》(已下线)专题06 平面向量在解析几何中的应用(第五篇)-2020高考数学压轴题命题区间探究与突破(已下线)专题11 解析几何与平面向量相结合问题(第五篇)-备战2020年高考数学大题精做之解答题题型全覆盖湖北省武汉市蔡甸区汉阳一中2021届高三下学期二模数学试题陕西省宝鸡市千阳中学2021届高三下学期第五次适应训练理科数学试题陕西省宝鸡市千阳中学2021届高三下学期第六次适应性训练理科数学试题广西桂林示范性高中十二校联盟2021-2022学年高二下学期入学检测数学(理)试题四川省宜宾市第四中学校2022-2023学年高二上学期第三学月考试数学(理)试题四川省宜宾市第四中学校2022-2023学年高二上学期第三学月考试数学(文)试题四川省泸县第五中学2022-2023学年高二下学期开学考试数学(文)试题四川省泸县第五中学2022-2023学年高二下学期开学考试数学(理)试题



