名校
1 . 已知 ,则
,则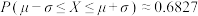 ,
,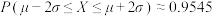 ,
,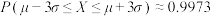 .今有一批数量庞大的零件.假设这批零件的某项质量指标引单位:毫米)服从正态分布
.今有一批数量庞大的零件.假设这批零件的某项质量指标引单位:毫米)服从正态分布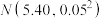 ,现从中随机抽取N个,这N个零件中恰有K个的质量指标ξ位于区间
,现从中随机抽取N个,这N个零件中恰有K个的质量指标ξ位于区间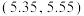 .若
.若 ,试以使得
,试以使得 最大的N值作为N的估计值,则N为( )
最大的N值作为N的估计值,则N为( )
 ,则
,则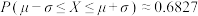 ,
,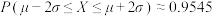 ,
,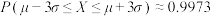 .今有一批数量庞大的零件.假设这批零件的某项质量指标引单位:毫米)服从正态分布
.今有一批数量庞大的零件.假设这批零件的某项质量指标引单位:毫米)服从正态分布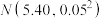 ,现从中随机抽取N个,这N个零件中恰有K个的质量指标ξ位于区间
,现从中随机抽取N个,这N个零件中恰有K个的质量指标ξ位于区间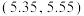 .若
.若 ,试以使得
,试以使得 最大的N值作为N的估计值,则N为( )
最大的N值作为N的估计值,则N为( )| A.45 | B.53 | C.54 | D.90 |
您最近一年使用:0次
2023-04-10更新
|
4968次组卷
|
13卷引用:模块九 第4套 1单选 2多选 2填空 2解答题(概率 导数)
(已下线)模块九 第4套 1单选 2多选 2填空 2解答题(概率 导数)广东省广州市从化区从化中学2023届考前仿真模拟3数学试题(已下线)第四篇 概率与统计 专题7 常见分布 微点3 常见分布综合训练(已下线)第08讲 两点分布、二项分布、超几何分布与正态分布(十一大题型)(讲义)-2(已下线)第七节 二项分布、超几何分布与正态分布 B卷素养养成卷 一轮点点通(已下线)随机变量及其分布专题15离散型随机变量的分布列(已下线)专题04 超几何分布+二项分布+正态分布压轴题(3)(已下线)【练】专题四 概率统计中的范围与最值问题(压轴大全)(已下线)第三章 随机变量及其分布列 专题三 重要的概率分布模型 微点3 重要的概率分布模型综合训练【基础版】(已下线)第五章 概率统计创新问题 专题三 概率统计中的函数思想 微点3 概率统计中的函数思想综合训练【基础版】福建省2023届高三毕业班适应性练习卷(省质检)数学试题福建省宁德市福鼎第六中学2022-2023学年高二下学期6月月考数学试题
2 . 为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布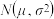 .
.
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在 之外的零件数,求
之外的零件数,求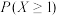 及X的数学期望;
及X的数学期望;
(2)一天内抽检零件中,如果出现了尺寸在 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)试说明上述监控生产过程方法的合理性;
(ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:
经计算得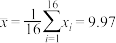 ,
,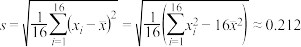 ,其中xi为抽取的第i个零件的尺寸,
,其中xi为抽取的第i个零件的尺寸,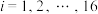 .
.
用样本平均数 作为μ的估计值
作为μ的估计值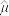 ,用样本标准差s作为σ的估计值
,用样本标准差s作为σ的估计值 ,利用估计值判断是否需对当天的生产过程进行检查?剔除
,利用估计值判断是否需对当天的生产过程进行检查?剔除 之外的数据,用剩下的数据估计μ和σ(精确到0.01).
之外的数据,用剩下的数据估计μ和σ(精确到0.01).
附:若随机变量Z服从正态分布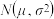 ,则
,则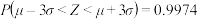 ,
,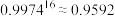 ,
,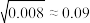 .
.
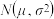 .
.(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在
 之外的零件数,求
之外的零件数,求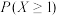 及X的数学期望;
及X的数学期望;(2)一天内抽检零件中,如果出现了尺寸在
 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.(ⅰ)试说明上述监控生产过程方法的合理性;
(ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:
| 9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
| 10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
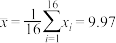 ,
,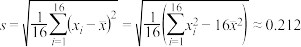 ,其中xi为抽取的第i个零件的尺寸,
,其中xi为抽取的第i个零件的尺寸,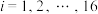 .
.用样本平均数
 作为μ的估计值
作为μ的估计值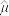 ,用样本标准差s作为σ的估计值
,用样本标准差s作为σ的估计值 ,利用估计值判断是否需对当天的生产过程进行检查?剔除
,利用估计值判断是否需对当天的生产过程进行检查?剔除 之外的数据,用剩下的数据估计μ和σ(精确到0.01).
之外的数据,用剩下的数据估计μ和σ(精确到0.01).附:若随机变量Z服从正态分布
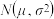 ,则
,则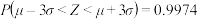 ,
,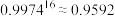 ,
,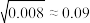 .
.
您最近一年使用:0次
2020-07-11更新
|
20605次组卷
|
64卷引用:甘肃省兰州市第一中学2016-2017学年高二下学期期末考试数学(理)试题
甘肃省兰州市第一中学2016-2017学年高二下学期期末考试数学(理)试题2017年全国普通高等学校招生统一考试理科数学(新课标1卷精编版)甘肃省兰州市第十中学2016-2017学年第二学期期末考试高二数学(理)试题2018年高考数学(理科,通用版)练酷专题二轮复习课时跟踪检测:(二十) 概率与统计【全国百强校】宁夏银川一中2017-2018学年高二下学期期中数学(理)试卷(已下线)《考前20天终极攻略》5月30日 概率【理科】(已下线)《高频考点解密》—解密25 概率(已下线)考点38 正态分布和条件概率(练习)-2021年高考数学复习一轮复习笔记(已下线)突破2.4正态分步-突破满分数学之2019-2020学年高二数学(理)重难点突破(人教A版选修2-3)(已下线)突破2.4正态分布突破满分数学之2019-2020学年高二数学(理)课时训练(人教A版选修2-3)(已下线)综合测试卷(巅峰版) -突破满分数学之2019-2020学年高二数学(理)课时训练(人教A版选修2-3)(已下线)专题16 概率与统计综合-五年(2016-2020)高考数学(理)真题分项(已下线)专题32 概率和统计【理】-十年(2011-2020)高考真题数学分项(六)(已下线)专题19 概率与统计综合-2020年高考数学(理)母题题源解密(全国Ⅰ专版)(已下线)专题11.7 二项分布、正态分布(精练)-2021年新高考数学一轮复习学与练(已下线)专题11.7 二项分布、正态分布(练)-2021年新高考数学一轮复习讲练测(已下线)专题11.5 离散型随机变量的分布列、均值与方差(精讲)-2021年高考数学(理)一轮复习学与练(已下线)专题4.5 正态分布(B卷提升篇)-2020-2021学年高二数学选择性必修第二册同步单元AB卷(新教材人教B版)(已下线)第二章 随机变量及其分布【专项训练】-2020-2021学年高二数学(理)下学期期末专项复习(人教A版选修2-3)北师大版(2019) 选修第一册 必杀技 第六章 素养检测人教A版(2019) 选修第三册 必杀技 第七章检测(已下线)专题14 概率统计-十年(2012-2021)高考数学真题分项汇编(全国通用)(已下线)考向49 二项分布与正态分布(已下线)专题09 计数原理与概率与统计(理)-五年(2017-2021)高考数学真题分项汇编(文科+理科)(已下线)专题47 概率、随机变量及其分布-备战2022年高考数学一轮复习一网打尽之重点难点突破(已下线)专题46 随机变量及其分布-学会解题之高三数学万能解题模板【2022版】(已下线)第14讲 正态分布-【寒假自学课】2022年高二数学寒假精品课(苏教版2019选择性必修第二册)(已下线)专题20统计概率(理科)解答题20题-备战2022年高考数学冲刺横向强化精练精讲(已下线)第七章 随机变量及其分布(选拔卷)-【单元测试】2021-2022学年高二数学尖子生选拔卷(人教A版2019选择性必修第三册)(已下线)专题20统计概率解答题20题-备战2022年高考数学冲刺横向强化精练精讲(新高考专用)(已下线)专题52 盘点随机变量分布列及期望的问题——备战2022年高考数学二轮复习常考点专题突破人教A版(2019) 选修第三册 一蹴而就 第七章 单元整合(已下线)专题1 概率、二项分布与正态分布-学会解题之高三数学321训练体系【2022版】人教A版(2019) 选修第三册 过关斩将 第七章 7.4~7.5综合拔高练安徽省合肥市第八中学2022届高三下学期最后一卷保温理科数学试题(已下线)专题50:正态分布-2023届高考数学一轮复习精讲精练(新高考专用)(已下线)专题49:离散随机变量的均值与方差-2023届高考数学一轮复习精讲精练(新高考专用)(已下线)专题13 概率统计解答题(已下线)考点26 概率、二项分布与正态分布-1-(核心考点讲与练)-2023年高考数学一轮复习核心考点讲与练(新高考专用)2023版 湘教版(2019) 选修第二册 过关斩将 第3章 综合拔高练(已下线)考向42 四大分布:两点分布、二项分布、超几何分布与正态分布(十大经典题型)-3(已下线)考向43二项分布、正太分布及其应用(重点)-3(已下线)考向42离散型随机变量的期望与方差(重点)-2(已下线)13.4 正态分布(已下线)第72讲 正态分布(已下线)专题11-1 直方图、回归方程(线性与非线性)-2(已下线)专题25 统计类(解答题)+概率(几何概型)-3(已下线)专题26 概率综合问题(分布列)(解答题)(理科)-3(已下线)第四篇 概率与统计 专题7 常见分布 微点1 常见分布(已下线)第08讲 两点分布、二项分布、超几何分布与正态分布(练习)单元测试B卷——第七章 随机变量及其分布(已下线)8.5 二项分布、超几何分布与正态分布(高考真题素材之十年高考)(已下线)专题25 概率统计解答题(理科)-2专题32概率统计解答题(第一部分)【巩固卷】第3章 概率高考强化 单元测试B-湘教版(2019)选择性必修第二册(已下线)第08讲 两点分布、二项分布、超几何分布与正态分布(十一大题型)(练习)-2云南省红河州泸西一中2017─2018学年高二上学期期末考试理科数学试题福建省泰宁第一中学2019-2020学年高二下学期第一次阶段考试数学试题新疆昌吉第九中学2021届高三上学期期中考试数学试题(已下线)复习题三4(已下线)解密16 随机变量及其分布(讲义)-【高频考点解密】2022年高考数学二轮复习讲义+分层训练(浙江专用)江苏省盐城市滨海中学2019-2020学年高二下学期期末模拟数学试题江苏省徐州市2022届高三下学期打靶试卷数学试题江苏省海安高级中学2023-2024学年高二下学期期中考试数学试卷
3 . 某市为了传承发展中华优秀传统文化,组织该市中学生进行了一次文化知识有奖竞赛,竞赛奖励规则如下:得分在 内的学生获三等奖,得分在
内的学生获三等奖,得分在 内的学生获二等奖,得分在
内的学生获二等奖,得分在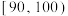 内的学生获得一等奖,其他学生不得奖,为了解学生对相关知识的掌握情况,随机抽取100名学生的竞赛成绩,并以此为样本绘制了样本频率分布直方图,如图所示.
内的学生获得一等奖,其他学生不得奖,为了解学生对相关知识的掌握情况,随机抽取100名学生的竞赛成绩,并以此为样本绘制了样本频率分布直方图,如图所示.
(2)若该市所有参赛学生的成绩X近似服从正态分布 ,其中
,其中 ,
, 为样本平均数的估计值,利用所得正态分布模型解决以下问题:
为样本平均数的估计值,利用所得正态分布模型解决以下问题:
(i)若该市共有10000名学生参加了竞赛,试估计参赛学生中成绩超过79分的学生数(结果四舍五入到整数);
(ii)若从所有参赛学生中(参赛学生数大于10000)随机取3名学生进行访谈,设其中竞赛成绩在64分以上的学生数为 ,求随机变量
,求随机变量 的分布列和期望.
的分布列和期望.
附参考数据,若随机变量X服从正态分布 ,则
,则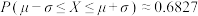 ,
,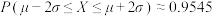 ,
,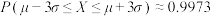 .
.
 内的学生获三等奖,得分在
内的学生获三等奖,得分在 内的学生获二等奖,得分在
内的学生获二等奖,得分在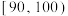 内的学生获得一等奖,其他学生不得奖,为了解学生对相关知识的掌握情况,随机抽取100名学生的竞赛成绩,并以此为样本绘制了样本频率分布直方图,如图所示.
内的学生获得一等奖,其他学生不得奖,为了解学生对相关知识的掌握情况,随机抽取100名学生的竞赛成绩,并以此为样本绘制了样本频率分布直方图,如图所示.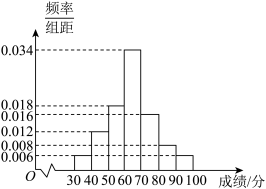
(2)若该市所有参赛学生的成绩X近似服从正态分布
 ,其中
,其中 ,
, 为样本平均数的估计值,利用所得正态分布模型解决以下问题:
为样本平均数的估计值,利用所得正态分布模型解决以下问题:(i)若该市共有10000名学生参加了竞赛,试估计参赛学生中成绩超过79分的学生数(结果四舍五入到整数);
(ii)若从所有参赛学生中(参赛学生数大于10000)随机取3名学生进行访谈,设其中竞赛成绩在64分以上的学生数为
 ,求随机变量
,求随机变量 的分布列和期望.
的分布列和期望.附参考数据,若随机变量X服从正态分布
 ,则
,则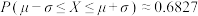 ,
,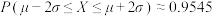 ,
,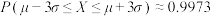 .
.
您最近一年使用:0次
2023-02-20更新
|
4131次组卷
|
11卷引用:广东省广州市天河区2021-2022学年高二下学期期末数学试题
广东省广州市天河区2021-2022学年高二下学期期末数学试题四川省内江市第六中学2022-2023学年高三上学期入学考试数学(理科)试题(已下线)专题50 正态分布-2山西省阳泉市2023届高三上学期期末数学试题湖南省长沙市雅礼中学2022-2023学年高三上学期月考(四)数学试题(已下线)第七章 随机变量及其分布 讲核心 02(已下线)7.5 正态分布 (精练)陕西省西安市西北工业大学附属中学2023届高三下学期第八次适应性训练理科数学试题河北省石家庄市正中实验中学2022-2023学年高二下学期4月月考数学试题(已下线)第七章 随机变量及其分布 讲核心 02辽宁省沈阳铁路实验中学2023-2024学年高二下学期4月阶段测试数学试卷
名校
解题方法
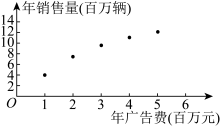
4 . 台州是全国三大电动车生产基地之一,拥有完整的产业链和突出的设计优势.某电动车公司为了抢占更多的市场份额,计划加大广告投入、该公司近5年的年广告费 (单位:百万元)和年销售量
(单位:百万元)和年销售量 (单位:百万辆)关系如图所示:令
(单位:百万辆)关系如图所示:令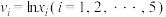 ,数据经过初步处理得:
,数据经过初步处理得:
现有①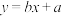 和②
和② 两种方案作为年销售量y关于年广告费x的回归分析模型,其中a,b,m,n均为常数.
两种方案作为年销售量y关于年广告费x的回归分析模型,其中a,b,m,n均为常数.
(1)请从相关系数的角度,分析哪一个模型拟合程度更好?
(2)根据(1)的分析选取拟合程度更好的回归分析模型及表中数据,求出y关于x的回归方程,并预测年广告费为6(百万元)时,产品的年销售量是多少?
(3)该公司生产的电动车毛利润为每辆200元(不含广告费、研发经费).该公司在加大广告投入的同时也加大研发经费的投入,年研发经费为年广告费的199倍.电动车的年净利润受年广告费和年研发经费影响外还受随机变量 影响,设随机变量
影响,设随机变量 服从正态分布
服从正态分布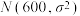 ,且满足
,且满足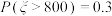 .在(2)的条件下,求该公司年净利润的最大值大于1000(百万元)的概率.(年净利润=毛利润×年销售量-年广告费-年研发经费-随机变量).
.在(2)的条件下,求该公司年净利润的最大值大于1000(百万元)的概率.(年净利润=毛利润×年销售量-年广告费-年研发经费-随机变量).
附:①相关系数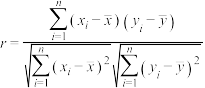 ,
,
回归直线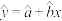 中公式分别为
中公式分别为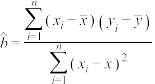 ,
, ;
;
②参考数据: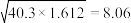 ,
,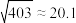 ,
, ,
, .
.
 (单位:百万元)和年销售量
(单位:百万元)和年销售量 (单位:百万辆)关系如图所示:令
(单位:百万辆)关系如图所示:令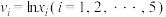 ,数据经过初步处理得:
,数据经过初步处理得:
 | 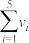 | 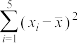 | 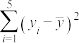 | 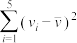 |  |  |
| 44 | 4.8 | 10 | 40.3 | 1.612 | 19.5 | 8.06 |
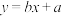 和②
和② 两种方案作为年销售量y关于年广告费x的回归分析模型,其中a,b,m,n均为常数.
两种方案作为年销售量y关于年广告费x的回归分析模型,其中a,b,m,n均为常数.(1)请从相关系数的角度,分析哪一个模型拟合程度更好?
(2)根据(1)的分析选取拟合程度更好的回归分析模型及表中数据,求出y关于x的回归方程,并预测年广告费为6(百万元)时,产品的年销售量是多少?
(3)该公司生产的电动车毛利润为每辆200元(不含广告费、研发经费).该公司在加大广告投入的同时也加大研发经费的投入,年研发经费为年广告费的199倍.电动车的年净利润受年广告费和年研发经费影响外还受随机变量
 影响,设随机变量
影响,设随机变量 服从正态分布
服从正态分布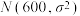 ,且满足
,且满足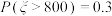 .在(2)的条件下,求该公司年净利润的最大值大于1000(百万元)的概率.(年净利润=毛利润×年销售量-年广告费-年研发经费-随机变量).
.在(2)的条件下,求该公司年净利润的最大值大于1000(百万元)的概率.(年净利润=毛利润×年销售量-年广告费-年研发经费-随机变量).附:①相关系数
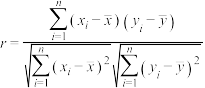 ,
,回归直线
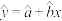 中公式分别为
中公式分别为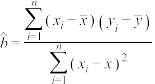 ,
, ;
;②参考数据:
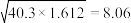 ,
,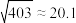 ,
, ,
, .
.
您最近一年使用:0次
2024-04-18更新
|
3756次组卷
|
11卷引用:浙江省台州市2024届高三下学期第二次教学质量评估数学试题
浙江省台州市2024届高三下学期第二次教学质量评估数学试题(已下线)第八章 成对数据的统计分析总结 第一练 考点强化训练(已下线)模块二 专题1统计案例中决策分析问题(北师大高二)(已下线)8.5 二项分布、超几何分布与正态分布(高考真题素材之十年高考)山西省太原市第五中学2023-2024学年高二下学期5月月考数学试题(已下线)专题04 第八章 成对数据的统计分析--高二期末考点大串讲(人教A版2019)(已下线)第八章 成对数据的统计分析(基础卷)-2023-2024学年高二数学下学期重难点突破及混淆易错规避(人教A版2019)湖北省武汉市黄陂区第七高级中学2024届高三模拟考试(二)数学试题(已下线)第四章 统计 专题四 相关分析与回归分析 微点3 相关分析与回归分析(三)【基础版】湖北省襄阳市第五中学2024届高三下学期第四次适应性测试数学试题云南省大理新世纪中学2024届高三数学模拟试题
名校
5 . 李明每天7:00从家里出发去学校,有时坐公交车,有时骑自行车.他各记录了50次坐公交车和骑自行车所花的时间,经数据分析得到:坐公交车平均用时30分钟,样本方差为36;自行车平均用时34分钟,样本方差为4.假设坐公交车用时X和骑自行车用时Y都服从正态分布,则( )
| A.P(X>32)>P(Y>32) |
| B.P(X≤36)=P(Y≤36) |
| C.李明计划7:34前到校,应选择坐公交车 |
| D.李明计划7:40前到校,应选择骑自行车 |
您最近一年使用:0次
2023-03-07更新
|
3874次组卷
|
18卷引用:专题22计数原理与概率与统计(多选题)
专题22计数原理与概率与统计(多选题)专题22计数原理与概率与统计(多选题)江苏省镇江市实验高级中学2022-2023学年高二下学期期末数学试题福建省福州市鼓山中学2023届高三下学期3月月考数学试题河北省邯郸市魏县第三中学2022-2023学年高二下学期5月月考数学试题(已下线)高二下学期期末复习选择题压轴题十九大题型专练(3)(已下线)2024年新课标全国Ⅰ卷数学真题变式题6-10广东省广州市真光中学2025届高三上学期开学质量检测数学试题(已下线)数学(新高考通用02)-2025届新高三开学摸底考试卷福建省厦门市2023届高三下学期第二次质量检测数学试题江苏省南通市海安高级中学2023届高三下学期一模数学试题江苏省南通市海安高级中学2023届高三下学期3月阶段测试(四)数学试题江苏省常州市戚墅堰高级中学2023届高三二模模拟数学试题浙江省宁波赫威斯肯特学校2022-2023学年高二普高部下学期第一次月考数学试题广西2024届高三高考桂柳鸿图模拟金卷试题(二)江苏省南通市部分学校2025届高三上学期8月联合统一调研测试数学试卷江苏省连云港市2023届高三下学期5月统一测试数学试题山东省济宁市邹城市北大新世纪高级中学2025届高三上学期开学考试数学试题
名校
6 . 面试是求职者进入职场的一个重要关口,也是机构招聘员工的重要环节.某科技企业招聘员工,首先要进行笔试,笔试达标者进入面试,面试环节要求应聘者回答3个问题,第一题考查对公司的了解,答对得2分,答错不得分,第二题和第三题均考查专业知识,每道题答对得4分,答错不得分.
(1)若一共有100人应聘,他们的笔试得分X服从正态分布 ,规定
,规定 为达标,求进入面试环节的人数大约为多少(结果四舍五入保留整数);
为达标,求进入面试环节的人数大约为多少(结果四舍五入保留整数);
(2)某进入面试的应聘者第一题答对的概率为 ,后两题答对的概率均为
,后两题答对的概率均为 ,每道题是否答对互不影响,求该应聘者的面试成绩Y的数学期望.
,每道题是否答对互不影响,求该应聘者的面试成绩Y的数学期望.
附:若 (
( ),则
),则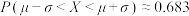 ,
,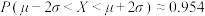 ,
,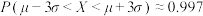 .
.
(1)若一共有100人应聘,他们的笔试得分X服从正态分布
 ,规定
,规定 为达标,求进入面试环节的人数大约为多少(结果四舍五入保留整数);
为达标,求进入面试环节的人数大约为多少(结果四舍五入保留整数);(2)某进入面试的应聘者第一题答对的概率为
 ,后两题答对的概率均为
,后两题答对的概率均为 ,每道题是否答对互不影响,求该应聘者的面试成绩Y的数学期望.
,每道题是否答对互不影响,求该应聘者的面试成绩Y的数学期望.附:若
 (
( ),则
),则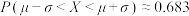 ,
,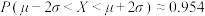 ,
,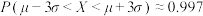 .
.
您最近一年使用:0次
2024-02-14更新
|
3524次组卷
|
13卷引用:2024年普通高等学校招生全国统一考试数学冲刺卷一(九省联考题型)
2024年普通高等学校招生全国统一考试数学冲刺卷一(九省联考题型)(已下线)7.5 正态分布(分层练习,8大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)专题8-2分布列综合归类-1河南省信阳市新县高级中学2024届高三下学期3月适应性考试数学试题湖南省长沙市长郡中学2024届高三下学期模拟(一)数学试卷江西省南昌市八一中学2024届高三下学期三模测试数学试题宁夏银川市六盘山高级中学2023-2024学年高二下学期5月月考数学试题江西省九师联盟2024届高三上学期1月质量检测试数学试题江西省宜春市上高二中2024届高三上学期期末数学试题(已下线)黄金卷02(2024新题型)湖南省衡阳市衡阳县第二中学2023-2024学年高二下学期期中达标数学测评卷广东省江门市新会第一中学2023-2024学年高二下学期期末考试数学试题福建省安溪第八中学2024-2025学年高三上学期8月份质量检测数学试题
名校
解题方法
7 . 已知某种机器的电源电压U(单位:V)服从正态分布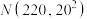 .其电压通常有3种状态:①不超过200V;②在200V~240V之间③超过240V.在上述三种状态下,该机器生产的零件为不合格品的概率分别为0.15,0.05,0.2.
.其电压通常有3种状态:①不超过200V;②在200V~240V之间③超过240V.在上述三种状态下,该机器生产的零件为不合格品的概率分别为0.15,0.05,0.2.
(1)求该机器生产的零件为不合格品的概率;
(2)从该机器生产的零件中随机抽取n( )件,记其中恰有2件不合格品的概率为
)件,记其中恰有2件不合格品的概率为 ,求
,求 取得最大值时n的值.
取得最大值时n的值.
附:若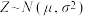 ,取
,取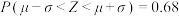 ,
,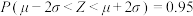 .
.
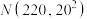 .其电压通常有3种状态:①不超过200V;②在200V~240V之间③超过240V.在上述三种状态下,该机器生产的零件为不合格品的概率分别为0.15,0.05,0.2.
.其电压通常有3种状态:①不超过200V;②在200V~240V之间③超过240V.在上述三种状态下,该机器生产的零件为不合格品的概率分别为0.15,0.05,0.2.(1)求该机器生产的零件为不合格品的概率;
(2)从该机器生产的零件中随机抽取n(
 )件,记其中恰有2件不合格品的概率为
)件,记其中恰有2件不合格品的概率为 ,求
,求 取得最大值时n的值.
取得最大值时n的值.附:若
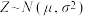 ,取
,取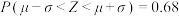 ,
,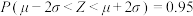 .
.
您最近一年使用:0次
2024-03-22更新
|
3403次组卷
|
6卷引用:7.5正态分布 第三课 知识扩展延伸
(已下线)7.5正态分布 第三课 知识扩展延伸(已下线)专题3.4正态分布(五个重难点突破)-2023-2024学年高二数学下学期重难点突破及混淆易错规避(人教A版2019)陕西省西安市陕西师范大学附属中学2023-2024学年高二下学期期中考试数学试卷江苏省南京市、盐城市2024届高三第一次模拟考试数学试题(已下线)数学(广东专用01,新题型结构)(已下线)专题06 离散型随机变量与正态分布--高二期末考点大串讲(苏教版2019选择性必修第二册)
名校
8 . 为了切实加强学校体育工作,促进学生积极参加体育锻炼,养成良好的锻炼习惯,某高中学校计划优化课程,增加学生体育锻炼时间,提高体质健康水平,某体质监测中心抽取了该较10名学生进行体质测试,得到如下表格:
记这10名学生体质测试成绩的平均分与方差分别为 ,
, ,经计算
,经计算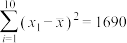 ,
,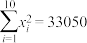 .
.
(1)求 ;
;
(2)规定体质测试成绩低于50分为不合格,从这10名学生中任取3名,记体质测试成绩不合格的人数为X,求X的分布列;
(3)经统计,高中生体质测试成绩近似服从正态分布 ,用
,用 ,
, 的值分别作为
的值分别作为 ,
, 的近似值,若监测中心计划从全市抽查100名高中生进行体质测试,记这100名高中生的体质测试成绩恰好落在区间
的近似值,若监测中心计划从全市抽查100名高中生进行体质测试,记这100名高中生的体质测试成绩恰好落在区间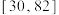 的人数为Y,求Y的数学期望
的人数为Y,求Y的数学期望 .附:若
.附:若 ,则
,则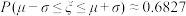 ,
,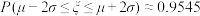 ,
,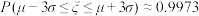 .
.
| 序号i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩 (分) (分) | 38 | 41 | 44 | 51 | 54 | 56 | 58 | 64 | 74 | 80 |
 ,
, ,经计算
,经计算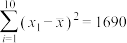 ,
,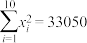 .
.(1)求
 ;
;(2)规定体质测试成绩低于50分为不合格,从这10名学生中任取3名,记体质测试成绩不合格的人数为X,求X的分布列;
(3)经统计,高中生体质测试成绩近似服从正态分布
 ,用
,用 ,
, 的值分别作为
的值分别作为 ,
, 的近似值,若监测中心计划从全市抽查100名高中生进行体质测试,记这100名高中生的体质测试成绩恰好落在区间
的近似值,若监测中心计划从全市抽查100名高中生进行体质测试,记这100名高中生的体质测试成绩恰好落在区间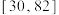 的人数为Y,求Y的数学期望
的人数为Y,求Y的数学期望 .附:若
.附:若 ,则
,则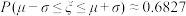 ,
,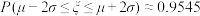 ,
,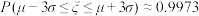 .
.
您最近一年使用:0次
2023-03-23更新
|
3349次组卷
|
6卷引用:山东省济南市2023届高三下学期3月一模数学试题
名校
解题方法
9 . 某网络 在平台开展了一项有奖闯关活动,并对每一关根据难度进行赋分,竞猜活动共五关,规定:上一关不通过则不进入下一关,本关第一次未通过有再挑战一次的机会,两次均未通过,则闯关失败,且各关能否通过相互独立,已知甲、乙、丙三人都参加了该项活动.
在平台开展了一项有奖闯关活动,并对每一关根据难度进行赋分,竞猜活动共五关,规定:上一关不通过则不进入下一关,本关第一次未通过有再挑战一次的机会,两次均未通过,则闯关失败,且各关能否通过相互独立,已知甲、乙、丙三人都参加了该项活动.
(1)若甲第一关通过的概率为 ,第二关通过的概率为
,第二关通过的概率为 ,求甲可以进入第三关的概率;
,求甲可以进入第三关的概率;
(2)已知该闯关活动累计得分服从正态分布,且满分为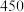 分,现要根据得分给共
分,现要根据得分给共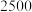 名参加者中得分前
名参加者中得分前 名发放奖励,
名发放奖励,
①假设该闯关活动平均分数为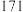 分,
分,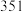 分以上共有
分以上共有 人,已知甲的得分为
人,已知甲的得分为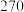 分,问甲能否获得奖励,请说明理由;
分,问甲能否获得奖励,请说明理由;
②丙得知他的分数为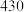 分,而乙告诉丙:“这次闯关活动平均分数为
分,而乙告诉丙:“这次闯关活动平均分数为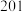 分,
分,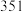 分以上共有
分以上共有 人”,请结合统计学知识帮助丙辨别乙所说信息的真伪.
人”,请结合统计学知识帮助丙辨别乙所说信息的真伪.
附:若随机变量 ,则
,则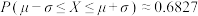 ;
;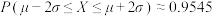 ;
;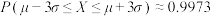 .
.
 在平台开展了一项有奖闯关活动,并对每一关根据难度进行赋分,竞猜活动共五关,规定:上一关不通过则不进入下一关,本关第一次未通过有再挑战一次的机会,两次均未通过,则闯关失败,且各关能否通过相互独立,已知甲、乙、丙三人都参加了该项活动.
在平台开展了一项有奖闯关活动,并对每一关根据难度进行赋分,竞猜活动共五关,规定:上一关不通过则不进入下一关,本关第一次未通过有再挑战一次的机会,两次均未通过,则闯关失败,且各关能否通过相互独立,已知甲、乙、丙三人都参加了该项活动.(1)若甲第一关通过的概率为
 ,第二关通过的概率为
,第二关通过的概率为 ,求甲可以进入第三关的概率;
,求甲可以进入第三关的概率;(2)已知该闯关活动累计得分服从正态分布,且满分为
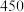 分,现要根据得分给共
分,现要根据得分给共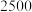 名参加者中得分前
名参加者中得分前 名发放奖励,
名发放奖励,①假设该闯关活动平均分数为
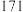 分,
分,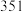 分以上共有
分以上共有 人,已知甲的得分为
人,已知甲的得分为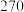 分,问甲能否获得奖励,请说明理由;
分,问甲能否获得奖励,请说明理由;②丙得知他的分数为
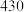 分,而乙告诉丙:“这次闯关活动平均分数为
分,而乙告诉丙:“这次闯关活动平均分数为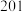 分,
分,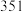 分以上共有
分以上共有 人”,请结合统计学知识帮助丙辨别乙所说信息的真伪.
人”,请结合统计学知识帮助丙辨别乙所说信息的真伪.附:若随机变量
 ,则
,则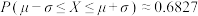 ;
;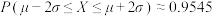 ;
;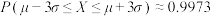 .
.
您最近一年使用:0次
2023-03-10更新
|
3245次组卷
|
6卷引用:专题9-1 概率与统计及分布列归类(理)(讲+练)-1
(已下线)专题9-1 概率与统计及分布列归类(理)(讲+练)-1(已下线)模拟检测卷03(理科)理科数学-【名校面对面】河南省三甲名校2023届高三校内模拟试题(五)(已下线)第三章 随机变量及其分布列 专题三 重要的概率分布模型 微点2 重要的概率分布模型(二)【基础版】重庆市2023届高高三第二次模拟数学试题(适用新高考)吉林省吉林市第一中学2023-2024学年高二下学期7月期末考试数学试题
名校
10 . 某公司为考核员工,采用某方案对员工进行业务技能测试,并统计分析测试成绩以确定员工绩效等级.
(1)已知该公司甲部门有3名负责人,乙部门有4名负责人,该公司从甲、乙两部门中随机选取3名负责人做测试分析,记负责人来自甲部门的人数为 ,求
,求 的最有可能的取值:
的最有可能的取值:
(2)该公司统计了七个部门测试的平均成绩 (满分100分)与绩效等级优秀率
(满分100分)与绩效等级优秀率 ,如下表所示:
,如下表所示:
根据数据绘制散点图,初步判断,选用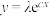 作为回归方程.令
作为回归方程.令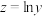 ,经计算得
,经计算得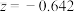 ,
,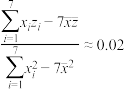
(ⅰ)已知某部门测试的平均成绩为60分,估计其绩效等级优秀率;
(ⅱ)根据统计分析,大致认为各部门测试平均成绩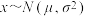 ,其中
,其中 近似为样本平均数
近似为样本平均数 ,
, 近似为样本方差
近似为样本方差 .经计算
.经计算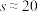 ,求某个部门绩效等级优秀率不低于
,求某个部门绩效等级优秀率不低于 的概率.
的概率.
参考公式与数据:①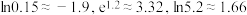 .
.
②线性回归方程 中,
中, ,
, .
.
③若随机变量 ,则
,则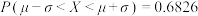 ,
, ,
, .
.
(1)已知该公司甲部门有3名负责人,乙部门有4名负责人,该公司从甲、乙两部门中随机选取3名负责人做测试分析,记负责人来自甲部门的人数为
 ,求
,求 的最有可能的取值:
的最有可能的取值:(2)该公司统计了七个部门测试的平均成绩
 (满分100分)与绩效等级优秀率
(满分100分)与绩效等级优秀率 ,如下表所示:
,如下表所示: | 32 | 41 | 54 | 68 | 74 | 80 | 92 |
 | 0.28 | 0.34 | 0.44 | 0.58 | 0.66 | 0.74 | 0.94 |
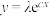 作为回归方程.令
作为回归方程.令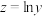 ,经计算得
,经计算得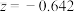 ,
,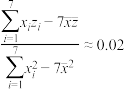
(ⅰ)已知某部门测试的平均成绩为60分,估计其绩效等级优秀率;
(ⅱ)根据统计分析,大致认为各部门测试平均成绩
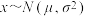 ,其中
,其中 近似为样本平均数
近似为样本平均数 ,
, 近似为样本方差
近似为样本方差 .经计算
.经计算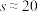 ,求某个部门绩效等级优秀率不低于
,求某个部门绩效等级优秀率不低于 的概率.
的概率.参考公式与数据:①
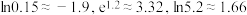 .
.②线性回归方程
 中,
中, ,
, .
.③若随机变量
 ,则
,则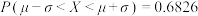 ,
, ,
, .
.
您最近一年使用:0次
2024-05-14更新
|
2845次组卷
|
6卷引用:山东省日照市2024届高三下学期校际联考(二模)数学试题
山东省日照市2024届高三下学期校际联考(二模)数学试题河南省信阳市新县高级中学2024届高三考前第六次适应性考试数学试题安徽省六安市霍山文峰学校2024届高三最后一卷数学试卷(已下线)模型4 以超几何分布为背景的离散型随机变量问题模型(第9章 计数原理、概率、随机变量及其分布 )河南省信阳市新县高级中学2025届高三上学期适应性考试(一)数学试题(已下线)第四章 统计 专题四 相关分析与回归分析 微点3 相关分析与回归分析(三)【基础版】



