在平面直角坐标系xOy中,有一个以为 和
和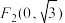 焦点、离心率为
焦点、离心率为 的椭圆.设椭圆在第一象限的部分为曲线C, 动点P在C上, C在点P处的切线与x , y轴的交点分别为A、B,且向量
的椭圆.设椭圆在第一象限的部分为曲线C, 动点P在C上, C在点P处的切线与x , y轴的交点分别为A、B,且向量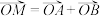 .求:
.求:
(1)点M的轨迹方程;
(2)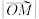 的最小值.
的最小值.
 和
和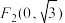 焦点、离心率为
焦点、离心率为 的椭圆.设椭圆在第一象限的部分为曲线C, 动点P在C上, C在点P处的切线与x , y轴的交点分别为A、B,且向量
的椭圆.设椭圆在第一象限的部分为曲线C, 动点P在C上, C在点P处的切线与x , y轴的交点分别为A、B,且向量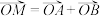 .求:
.求:(1)点M的轨迹方程;
(2)
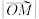 的最小值.
的最小值.
11-12高三上·全国·单元测试 查看更多[2]
更新时间:2016/12/01 00:42:33
|
相似题推荐
解答题-问答题
|
适中
(0.65)
【推荐1】已知曲线上一动点P(x,y)(x>0)到定点F(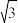 ,0)的距离与它到直线l:x
,0)的距离与它到直线l:x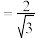 的距离的比是
的距离的比是 .
.
(1)求动点P的轨迹E的方程;
(2)若M是曲线E上的一个动点,直线l′:y=x+4,求点M到直线l′的距离的最小值.
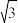 ,0)的距离与它到直线l:x
,0)的距离与它到直线l:x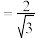 的距离的比是
的距离的比是 .
.(1)求动点P的轨迹E的方程;
(2)若M是曲线E上的一个动点,直线l′:y=x+4,求点M到直线l′的距离的最小值.
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
【推荐2】在平面直角坐标系 中,已知圆
中,已知圆 在
在 轴上截得线段长为
轴上截得线段长为 ,在
,在 轴上截得线段长为
轴上截得线段长为 .
.
(Ⅰ)求圆心 的轨迹方程;
的轨迹方程;
(Ⅱ)若圆心 到直线
到直线 的距离为
的距离为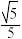 ,求圆
,求圆 的方程.
的方程.
 中,已知圆
中,已知圆 在
在 轴上截得线段长为
轴上截得线段长为 ,在
,在 轴上截得线段长为
轴上截得线段长为 .
.(Ⅰ)求圆心
 的轨迹方程;
的轨迹方程;(Ⅱ)若圆心
 到直线
到直线 的距离为
的距离为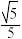 ,求圆
,求圆 的方程.
的方程.
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
名校
解题方法
【推荐1】已知椭圆 的左,右焦点分别为
的左,右焦点分别为 ,
, ,点
,点 在椭圆
在椭圆 上,
上,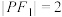 ,
, ,且椭圆
,且椭圆 的离心率为
的离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2)设过点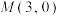 的直线
的直线 与椭圆
与椭圆 相交于
相交于 ,
, 两点,求
两点,求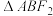 面积的最大值.
面积的最大值.
 的左,右焦点分别为
的左,右焦点分别为 ,
, ,点
,点 在椭圆
在椭圆 上,
上,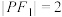 ,
, ,且椭圆
,且椭圆 的离心率为
的离心率为 .
.(1)求椭圆
 的方程;
的方程;(2)设过点
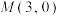 的直线
的直线 与椭圆
与椭圆 相交于
相交于 ,
, 两点,求
两点,求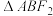 面积的最大值.
面积的最大值.
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
解题方法
【推荐2】已知A、B分别为椭圆 :
: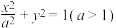 )的上、下顶点,F是椭圆
)的上、下顶点,F是椭圆 的右焦点,C是椭圆
的右焦点,C是椭圆 上异于A、B的点,点D在坐标平面内.
上异于A、B的点,点D在坐标平面内.
(1)若 ,求椭圆
,求椭圆 的标准方程;
的标准方程;
(2)若 ,且
,且 ,
, ,求四边形CADB面积S的最大值.
,求四边形CADB面积S的最大值.
 :
: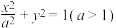 )的上、下顶点,F是椭圆
)的上、下顶点,F是椭圆 的右焦点,C是椭圆
的右焦点,C是椭圆 上异于A、B的点,点D在坐标平面内.
上异于A、B的点,点D在坐标平面内.(1)若
 ,求椭圆
,求椭圆 的标准方程;
的标准方程;(2)若
 ,且
,且 ,
, ,求四边形CADB面积S的最大值.
,求四边形CADB面积S的最大值.
您最近一年使用:0次

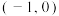 和
和 ,动点
,动点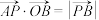 (
( 为坐标原点).
为坐标原点). 的方程;
的方程;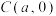 为
为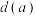 ;
;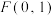 的直线
的直线 、
、 两点,线段
两点,线段 的垂直平分线与
的垂直平分线与 点,求
点,求 ,上、下顶点分别为
,上、下顶点分别为 ,若
,若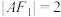 ,点
,点 关于直线
关于直线 的对称点在椭圆
的对称点在椭圆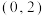 作直线
作直线 ;若
;若 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.


