2024高三·全国·专题练习
解题方法
1 . 求下列函数的解析式
(1)已知 ,则
,则
________ .
(2)已知 是三次函数,且在
是三次函数,且在 处的极值为0,在
处的极值为0,在 处的极值为1,则
处的极值为1,则
______ .
(3)已知 的定义域为
的定义域为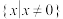 ,满足
,满足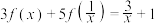 ,则函数
,则函数
________ .
(4)已知函数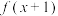 是偶函数,且
是偶函数,且 时
时 ,则
,则 时,
时,
________ .
(5)已知函数 的定义域为R,且
的定义域为R,且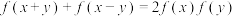 ,
, ,请写出满足条件的一个
,请写出满足条件的一个
______ (答案不唯一).
(1)已知
 ,则
,则
(2)已知
 是三次函数,且在
是三次函数,且在 处的极值为0,在
处的极值为0,在 处的极值为1,则
处的极值为1,则
(3)已知
 的定义域为
的定义域为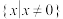 ,满足
,满足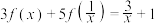 ,则函数
,则函数
(4)已知函数
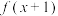 是偶函数,且
是偶函数,且 时
时 ,则
,则 时,
时,
(5)已知函数
 的定义域为R,且
的定义域为R,且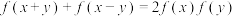 ,
, ,请写出满足条件的一个
,请写出满足条件的一个
您最近一年使用:0次
名校
解题方法
2 . 已知函数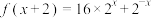 .
.
(1)求 的解析式;
的解析式;
(2)判断 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(3)设函数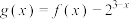 ,若
,若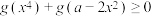 ,求a的取值范围.
,求a的取值范围.
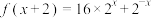 .
.(1)求
 的解析式;
的解析式;(2)判断
 的奇偶性,并说明理由;
的奇偶性,并说明理由;(3)设函数
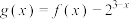 ,若
,若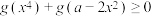 ,求a的取值范围.
,求a的取值范围.
您最近一年使用:0次
7日内更新
|
491次组卷
|
2卷引用:黑龙江省龙东联盟2023-2024学年高二下学期期末数学试题
名校
解题方法
3 . 已知函数 满足
满足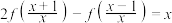 ,则
,则
__________ .
 满足
满足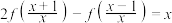 ,则
,则
您最近一年使用:0次
解题方法
4 . (1)已知 是二次函数,且满足
是二次函数,且满足 ,
,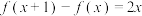 ,求
,求 的表达式;
的表达式;
(2)已知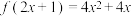 ,求
,求 的表达式;
的表达式;
(3)已知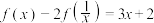 ,求
,求 的表达式.
的表达式.
 是二次函数,且满足
是二次函数,且满足 ,
,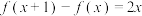 ,求
,求 的表达式;
的表达式;(2)已知
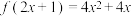 ,求
,求 的表达式;
的表达式;(3)已知
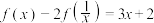 ,求
,求 的表达式.
的表达式.
您最近一年使用:0次
解题方法
5 . (1)已知 是一次函数,且
是一次函数,且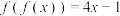 ,求
,求 的表达式;
的表达式;
(2)已知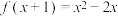 ,求
,求 的表达式;
的表达式;
(3)已知 ,求
,求 的表达式;
的表达式;
(4)已知 ,求
,求 的表达式.
的表达式.
 是一次函数,且
是一次函数,且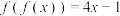 ,求
,求 的表达式;
的表达式;(2)已知
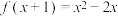 ,求
,求 的表达式;
的表达式;(3)已知
 ,求
,求 的表达式;
的表达式;(4)已知
 ,求
,求 的表达式.
的表达式.
您最近一年使用:0次
解题方法
6 . 回答下面两个题:
(1)已知函数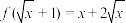 ,求
,求 的解析式;
的解析式;
(2)已知 为R上的奇函数,当
为R上的奇函数,当 时,
时, .求
.求 的解析式;
的解析式;
(1)已知函数
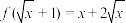 ,求
,求 的解析式;
的解析式;(2)已知
 为R上的奇函数,当
为R上的奇函数,当 时,
时, .求
.求 的解析式;
的解析式;
您最近一年使用:0次
解题方法
7 . 满足 的非零有理系数多项式
的非零有理系数多项式 的最低次数为
的最低次数为________ .
 的非零有理系数多项式
的非零有理系数多项式 的最低次数为
的最低次数为
您最近一年使用:0次
解题方法
8 . 已知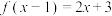 ,
,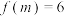 ,则
,则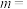 ( )
( )
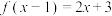 ,
,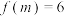 ,则
,则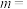 ( )
( )A.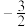 | B. | C. | D. |
您最近一年使用:0次
名校
解题方法
9 . 已知函数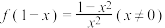 ,则
,则 ( )
( )
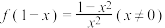 ,则
,则 ( )
( )A.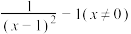 | B. |
C.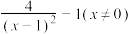 | D.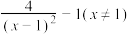 |
您最近一年使用:0次
2024-07-04更新
|
875次组卷
|
13卷引用:重庆市2023届高三临门一卷(三)数学试题
重庆市2023届高三临门一卷(三)数学试题(已下线)第02讲 3.1.2函数的表示法(精讲精练)(2) -【帮课堂】(已下线)专题 3-2 函数图像与解析式及其应用归类(1) - 【巅峰课堂】题型归纳与培优练(已下线)第一篇“必拿”选择前5填空前2 专题7 函数的定义域与解析式【讲】(已下线)专题02 函数及其应用、指对幂函数(5大易错点分析+解题模板+举一反三+易错题通关)(已下线)第01讲 3.1函数的概念及其表示(2) - -【练透核心考点】(已下线)专题2.1 函数的解析式与定义域、值域【八大题型】天津市第三中学2023-2024学年高二下学期6月月考数学试题(已下线)第01讲 函数的概念及其表示(十六大题型)(讲义)-1(已下线)必考考点10 函数(一轮复习) 专题讲解 (期末考试必考的10大核心考点) (已下线)第13讲 函数的表示方法(1)-【暑假自学课】(苏教版2019必修第一册)(已下线)热点专题 2-1 函数的基本概念及其性质(解析式,定义域,值域)-1(已下线)第10讲 函数及其表示方法-【暑假自学课】(人教B版2019必修第一册)
2024高三·全国·专题练习
解题方法
10 . 已知 ,求
,求 的解析式
的解析式
 ,求
,求 的解析式
的解析式
您最近一年使用:0次



