名校
1 . 如图,摩天轮上一点P在时刻t(单位:分钟)距离地面的高度y(单位:米)满足 ,已知该摩天轮的半径为50米,圆心O距地面的高度为60米,摩天轮做匀速转动,每3分钟转一圈,点P的起始位置在摩天轮的最低点处.
,已知该摩天轮的半径为50米,圆心O距地面的高度为60米,摩天轮做匀速转动,每3分钟转一圈,点P的起始位置在摩天轮的最低点处.

(1)根据条件写出y关于t的函数解析式;
(2)在摩天轮转动的一圈内,有多长时间点P距离地面的高度超过85米?
 ,已知该摩天轮的半径为50米,圆心O距地面的高度为60米,摩天轮做匀速转动,每3分钟转一圈,点P的起始位置在摩天轮的最低点处.
,已知该摩天轮的半径为50米,圆心O距地面的高度为60米,摩天轮做匀速转动,每3分钟转一圈,点P的起始位置在摩天轮的最低点处.
(1)根据条件写出y关于t的函数解析式;
(2)在摩天轮转动的一圈内,有多长时间点P距离地面的高度超过85米?
您最近一年使用:0次
2020-04-02更新
|
1582次组卷
|
13卷引用:2015届上海市青浦区高三上学期期终学习质量调研数学试卷
2015届上海市青浦区高三上学期期终学习质量调研数学试卷2015届湖南省长望浏宁四县高三3月调研(一模)考试理科数学试卷上海市上海师范大学附属中学2018-2019学年高三下学期质量检测数学试题上海市上海师范大学附属中学2018-2019学年高三上学期10月月考数学试题上海市交大附中2017-2018学年高一下学期期中数学试题山东省济南市市中区实验中学2018-2019学年高一下学期期中数学试题(已下线)专题03 三角函数中的实际应用问题(第一篇)-备战2020年高考数学大题精做之解答题题型全覆盖辽宁省锦州市2019-2020学年高一(下)期末数学试题(已下线)5.7+三角函数的应用-2020-2021高中数学新教材配套提升训练(人教A版必修第一册)上海市晋元高级中学2022届高三下学期3月月考数学试题上海市上海中学2022届高三下学期高考模拟3数学试题上海市外国语大学附属外国语学校2022-2023学年高一下学期期中数学试题上海市华东师范大学周浦中学2022-2023学年高一下学期期末数学试题
名校
解题方法
2 . 对于函数 ,在使
,在使 成立的所有常数
成立的所有常数 中,我们把
中,我们把 的最大值称为函数
的最大值称为函数 的“下确界”.若函数
的“下确界”.若函数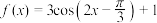 ,
,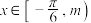 的“下确界”为
的“下确界”为 ,则
,则 的取值范围是( )
的取值范围是( )
 ,在使
,在使 成立的所有常数
成立的所有常数 中,我们把
中,我们把 的最大值称为函数
的最大值称为函数 的“下确界”.若函数
的“下确界”.若函数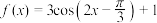 ,
,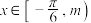 的“下确界”为
的“下确界”为 ,则
,则 的取值范围是( )
的取值范围是( )A.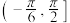 | B.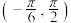 | C.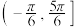 | D.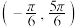 |
您最近一年使用:0次
2020-03-05更新
|
1019次组卷
|
10卷引用:吉林省吉林市桦甸市第四中学2018-2019学年高一下学期期末数学试题
吉林省吉林市桦甸市第四中学2018-2019学年高一下学期期末数学试题广西来宾市2018-2019学年高一下学期期末教学质量调研考试数学试题江西省新余市第一中学2019-2020学年高一3月零班网上摸底考试数学试题吉林省舒兰市实验中学2019-2020学年高一下学期期中考试数学试题辽宁省铁岭市调兵山市第一高级中学2019-2020学年高一下学期第一次月考数学试题(已下线)专题5.7 三角函数的应用-《讲亮点》2021-2022学年高一数学新教材同步配套讲练(人教A版2019必修第一册)陕西省延安北大培文学校2021-2022学年高一下学期第三次月考数学试题1.8三角函数的简单应用-【培优题】2020-2021学年高一数学北师大2019版第二册四川省射洪中学校2022-2023学年高一下学期期中数学试题内蒙古赤峰市敖汉旗新惠中学2023-2024学年高一下学期4月月考数学试题
3 . 如图,半径为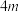 的水轮绕着圆心
的水轮绕着圆心 按逆时针方向做匀速圆周运动,每分钟转动
按逆时针方向做匀速圆周运动,每分钟转动 圈,圆心
圈,圆心 距离水面
距离水面 ,水轮上点
,水轮上点 从离开水面的时刻
从离开水面的时刻 开始计算时间.
开始计算时间.
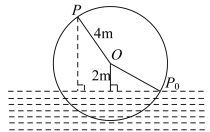
(1)试用正弦函数模型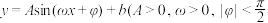 ,写出点
,写出点 距离水面的高度
距离水面的高度 与时间
与时间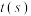 满足的函数关系式;
满足的函数关系式;
(2)求点 第一次到达最高点需要的时间.
第一次到达最高点需要的时间.
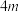 的水轮绕着圆心
的水轮绕着圆心 按逆时针方向做匀速圆周运动,每分钟转动
按逆时针方向做匀速圆周运动,每分钟转动 圈,圆心
圈,圆心 距离水面
距离水面 ,水轮上点
,水轮上点 从离开水面的时刻
从离开水面的时刻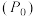 开始计算时间.
开始计算时间.
(1)试用正弦函数模型
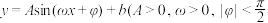 ,写出点
,写出点 距离水面的高度
距离水面的高度 与时间
与时间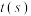 满足的函数关系式;
满足的函数关系式;(2)求点
 第一次到达最高点需要的时间.
第一次到达最高点需要的时间.
您最近一年使用:0次
4 . 如图,某港口一天6时到18时的水深变化曲线近似满足函数关系式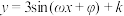 ,据此可知,这段时间水深(单位:
,据此可知,这段时间水深(单位: )的最大值为( )
)的最大值为( )
 ,据此可知,这段时间水深(单位:
,据此可知,这段时间水深(单位: )的最大值为( )
)的最大值为( )
| A.5 | B.6 | C.8 | D.10 |
您最近一年使用:0次
2020-02-29更新
|
619次组卷
|
21卷引用:高中数学人教A版必修4 第一章 三角函数 1.6 三角函数模型的简单应用
高中数学人教A版必修4 第一章 三角函数 1.6 三角函数模型的简单应用(已下线)2019年一轮复习讲练测【新课标版理】 三角函数的图象及三角函数模型的简单应用【练】(已下线)2019年一轮复习讲练测【新课标版文】4.4三角函数的图象及三角函数模型的简单应用【练】(已下线)2019年一轮复习讲练测 4.5 函数y=Asin(ωx+φ)的图象及三角函数模型的简单应用【浙江版】 【练】(已下线)2019高考备考一轮复习精品资料 【理】专题十九 函数y=Asin(ωx+φ)的图象 教学案(已下线)2019高考热点题型和提分秘籍 【理数】专题16 函数y=Asin(ωx+φ)的图象及应用 (教学案)(已下线)2019高考热点题型和提分秘籍 【文数】专题16 函数y=Asin(ωx+φ)的图象及应用 (教学案)步步高高一数学暑假作业:作业21 三角函数模型的简单应用人教A版 必杀技 第一章 三角函数 1.6 三角函数模型的简单应用人教A版(2019) 必修第一册 必杀技 第五章 5.7 三角函数的应用(已下线)3.3 正弦定理 余弦定理与解三角形 [理]-《备战2020年高考精选考点专项突破题集》第五章 三角函数 5.7 三角函数的应用山东省烟台市2019-2020学年高一上学期期末数学试题人教B版(2019) 必修第三册 过关斩将 第七章 三角函数 7.4 数学建模活动:周期现象的描述2020届河南省平顶山许昌济源高三第一次质量检测数学(理)试题山东省济宁市微山县第一中学2019-2020学年高一下学期网络课堂第一阶段网络测试数学试题(已下线)考点23 三角函数的图像与性质、三角函数模型的应用(考点专练)-备战2021年新高考数学一轮复习考点微专题(已下线)5.7+三角函数的应用-2020-2021学年高一数学新教材配套学案(人教A版必修第一册)北师大版(2019) 必修第二册 金榜题名 进阶篇 十三 三角函数的简单应用广西梧州市岑溪市2021-2022学年高一下学期期中考试数学试题2024年江苏省扬州市学业水平考试数学模拟试卷
5 . 如图所示,某摩天轮设施,其旋转半径为50米,最高点距离地面110米,开启后按逆时针方向匀速旋转,转一周大约21分钟. 某人在最低点的位置坐上摩天轮的座舱,并开始计时,则第7分钟时他距离地面的高度大约为( )


| A.75米 | B.85米 |
C.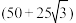 米 米 | D. 米 米 |
您最近一年使用:0次
2020-02-01更新
|
422次组卷
|
3卷引用:山东省滨州市2019-2020学年高一上学期期末数学试题
名校
6 . 如图所示,有一块等腰直角三角形地块ABC, ,BC长2千米,现对这块地进行绿化改造,计划从BC的中点D引出两条成45°的线段DE和DF,与AB和AC围成四边形区域AEDF,在该区域内种植花卉,其余区域种植草坪;设
,BC长2千米,现对这块地进行绿化改造,计划从BC的中点D引出两条成45°的线段DE和DF,与AB和AC围成四边形区域AEDF,在该区域内种植花卉,其余区域种植草坪;设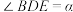 ,试求花卉种植面积
,试求花卉种植面积 的取值范围.
的取值范围.
 ,BC长2千米,现对这块地进行绿化改造,计划从BC的中点D引出两条成45°的线段DE和DF,与AB和AC围成四边形区域AEDF,在该区域内种植花卉,其余区域种植草坪;设
,BC长2千米,现对这块地进行绿化改造,计划从BC的中点D引出两条成45°的线段DE和DF,与AB和AC围成四边形区域AEDF,在该区域内种植花卉,其余区域种植草坪;设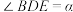 ,试求花卉种植面积
,试求花卉种植面积 的取值范围.
的取值范围.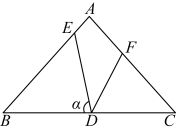
您最近一年使用:0次
2020-01-15更新
|
1549次组卷
|
8卷引用:山东省泰安市2019-2020学年高三上学期期末数学试题
山东省泰安市2019-2020学年高三上学期期末数学试题2020届高三2月第01期(考点04)(理科)-《新题速递·数学》山西省大同市第一中学2019-2020学年高三下学期模拟(六)数学(理)试题(已下线)专题03 三角函数中的实际应用问题(第一篇)-备战2020年高考数学大题精做之解答题题型全覆盖山东省济南市莱芜第一中学2020-2021学年高三上学期11月月考数学试题(已下线)黄金卷05 【赢在高考·黄金20卷】备战2021年高考数学全真模拟卷(广东专用)江苏省无锡市天一中学2021-2022学年高一强化班下学期期中数学试题江苏省镇江市扬中市第二高级中学2021-2022学年高一下学期期末适应性测试数学试题
名校
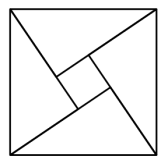
7 . 我国古代数学家赵爽的弦图是由四个全等的直角三角形与-一个小正方形拼成的一个大正方形(如图).如果小正方形的边长为 ,大正方形的边长为
,大正方形的边长为 ,直角三角形中较小的锐角为
,直角三角形中较小的锐角为 ,则
,则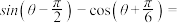 ( )
( )
 ,大正方形的边长为
,大正方形的边长为 ,直角三角形中较小的锐角为
,直角三角形中较小的锐角为 ,则
,则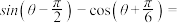 ( )
( )
A.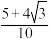 | B.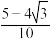 |
C.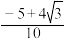 | D.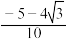 |
您最近一年使用:0次
2019-12-27更新
|
927次组卷
|
7卷引用:湖北省华师一附中、黄冈中学等八校2019-2020学年高三第一次联考数学(文)试题
名校
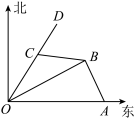
8 . 如图,港口 在港口
在港口 的正东120海里处,小岛
的正东120海里处,小岛 在港口
在港口 的北偏东
的北偏东 的方向,且在港口
的方向,且在港口 北偏西
北偏西 的方向上,一艘科学考察船从港口
的方向上,一艘科学考察船从港口 出发,沿北偏东
出发,沿北偏东 的
的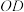 方向以20海里/小时的速度驶离港口
方向以20海里/小时的速度驶离港口 .一艘给养快艇从港口
.一艘给养快艇从港口 以60海里/小时的速度驶向小岛
以60海里/小时的速度驶向小岛 ,在
,在 岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时.
岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时.
(1)求给养快艇从港口 到小岛
到小岛 的航行时间;
的航行时间;
(2)给养快艇驶离港口 后,最少经过多少小时能和科考船相遇?
后,最少经过多少小时能和科考船相遇?
 在港口
在港口 的正东120海里处,小岛
的正东120海里处,小岛 在港口
在港口 的北偏东
的北偏东 的方向,且在港口
的方向,且在港口 北偏西
北偏西 的方向上,一艘科学考察船从港口
的方向上,一艘科学考察船从港口 出发,沿北偏东
出发,沿北偏东 的
的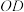 方向以20海里/小时的速度驶离港口
方向以20海里/小时的速度驶离港口 .一艘给养快艇从港口
.一艘给养快艇从港口 以60海里/小时的速度驶向小岛
以60海里/小时的速度驶向小岛 ,在
,在 岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时.
岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时.
(1)求给养快艇从港口
 到小岛
到小岛 的航行时间;
的航行时间;(2)给养快艇驶离港口
 后,最少经过多少小时能和科考船相遇?
后,最少经过多少小时能和科考船相遇?
您最近一年使用:0次
2019-11-21更新
|
531次组卷
|
4卷引用:河南省郑州市第一中学2019-2020学年高二上学期期中数学(理)试题
名校
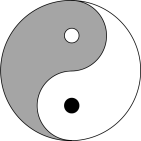
9 . 中国传统文化中很多内容体现了数学的“对称美”.如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分体现了相互变化、对称统一的形式美、和谐美.给出定义:能够将圆 (
( 为坐标原点)的周长和面积同时平分的函数称为这个圆的“优美函数”.给出下列命题:
为坐标原点)的周长和面积同时平分的函数称为这个圆的“优美函数”.给出下列命题:
①对于任意一个圆 ,其“优美函数”有无数个;
,其“优美函数”有无数个;
②函数 可以是某个圆的“优美函数”;
可以是某个圆的“优美函数”;
③正弦函数 可以同时是无数个圆的“优美函数”;
可以同时是无数个圆的“优美函数”;
④函数 是“优美函数”的充要条件为函数
是“优美函数”的充要条件为函数 的图象是中心对称图形.
的图象是中心对称图形.
 (
( 为坐标原点)的周长和面积同时平分的函数称为这个圆的“优美函数”.给出下列命题:
为坐标原点)的周长和面积同时平分的函数称为这个圆的“优美函数”.给出下列命题:①对于任意一个圆
 ,其“优美函数”有无数个;
,其“优美函数”有无数个;②函数
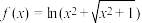 可以是某个圆的“优美函数”;
可以是某个圆的“优美函数”;③正弦函数
 可以同时是无数个圆的“优美函数”;
可以同时是无数个圆的“优美函数”;④函数
 是“优美函数”的充要条件为函数
是“优美函数”的充要条件为函数 的图象是中心对称图形.
的图象是中心对称图形.
| A.①④ | B.①③④ | C.②③ | D.①③ |
您最近一年使用:0次
2019-11-14更新
|
793次组卷
|
13卷引用:2017届河南省南阳、信阳等六市高三第一次联考理数试卷
2017届河南省南阳、信阳等六市高三第一次联考理数试卷2017届全国各地高三最新模拟文化试题集数学试卷2017届河南省南阳、信阳等六市高三第一次联考文数试卷河南省实验中学2019-2020学年高三上学期期中数学试题陕西省延安中学2020届高三下学期期末质量检测数学试题江苏省无锡市宜兴中学2020-2021学年高二上学期强基培训数学试题宁夏银川一中2021届高三第三次月考数学(文)试题宁夏银川一中2021届高三第三次月考数学(理)试题江苏省无锡市江阴市青阳高级中学2020-2021学年高一上学期12月阶段检测数学试题宁夏隆德县中学2021届高三年级上学期文科数学第三次月考试题新疆喀什区第二中学2021届高三上学期期中考试数学(理)试题上海市上海师范大学附属中学2021-2022学年高一上学期期末数学试题1.8三角函数的简单应用-【培优题】2020-2021学年高一数学北师大2019版第二册
名校
10 . 已知函数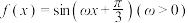 的最小正周期为
的最小正周期为 .
.
(1)求 的值;
的值;
(2)将函数 图象上各点的横坐标缩短到原来的
图象上各点的横坐标缩短到原来的 ,纵坐标不变,得到函数
,纵坐标不变,得到函数 的图象,求函数
的图象,求函数 在区间
在区间 上的最小值.
上的最小值.
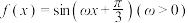 的最小正周期为
的最小正周期为 .
.(1)求
 的值;
的值;(2)将函数
 图象上各点的横坐标缩短到原来的
图象上各点的横坐标缩短到原来的 ,纵坐标不变,得到函数
,纵坐标不变,得到函数 的图象,求函数
的图象,求函数 在区间
在区间 上的最小值.
上的最小值.
您最近一年使用:0次
2019-11-06更新
|
1019次组卷
|
5卷引用:人教A版(2019) 必修第一册 突围者 第五章 第七节三角函数的应用
人教A版(2019) 必修第一册 突围者 第五章 第七节三角函数的应用黑龙江省哈尔滨市宾县一中2019-2020学年高一上学期第三次月考数学(文)试题黑龙江省哈尔滨市宾县一中2019-2020学年高一上学期第三次月考数学(理)试题甘肃省天水市第一中学2019-2020学年高一上学期期中数学(兰天班)试题(已下线)[新教材精创] 5.6 函数y=Asin(wx+φ)练习(2) -人教A版高中数学必修第一册



