名校
1 . 已知三次函数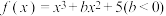 有极小值点
有极小值点 ,则下列说法中正确的有( )
,则下列说法中正确的有( )
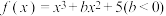 有极小值点
有极小值点 ,则下列说法中正确的有( )
,则下列说法中正确的有( )A.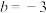 |
B.函数 有三个零点 有三个零点 |
C.函数 的对称中心为 的对称中心为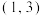 |
D.过 可以作两条直线与 可以作两条直线与 的图象相切 的图象相切 |
您最近一年使用:0次
解题方法
2 . 设 是函数
是函数 的导函数,
的导函数, 是函数
是函数 的导数,若方程
的导数,若方程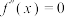 有实数解
有实数解 ,则称点
,则称点 为
为 的“拐点”.经过探究发现:任何一个三次函数都有“拐点”且“拐点”就是三次函数图象的对称中心.已知三次函数
的“拐点”.经过探究发现:任何一个三次函数都有“拐点”且“拐点”就是三次函数图象的对称中心.已知三次函数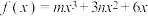 的对称中心为
的对称中心为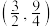 .
.
(1)求实数 ,
, 的值;
的值;
(2)求 的极值.
的极值.
 是函数
是函数 的导函数,
的导函数, 是函数
是函数 的导数,若方程
的导数,若方程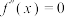 有实数解
有实数解 ,则称点
,则称点 为
为 的“拐点”.经过探究发现:任何一个三次函数都有“拐点”且“拐点”就是三次函数图象的对称中心.已知三次函数
的“拐点”.经过探究发现:任何一个三次函数都有“拐点”且“拐点”就是三次函数图象的对称中心.已知三次函数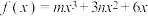 的对称中心为
的对称中心为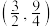 .
.(1)求实数
 ,
, 的值;
的值;(2)求
 的极值.
的极值.
您最近一年使用:0次
3 . 已知函数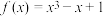 ,则( )
,则( )
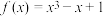 ,则( )
,则( )A. 有三个极值点 有三个极值点 | B. 有三个零点 有三个零点 |
C.点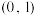 是曲线 是曲线 的对称中心 的对称中心 | D.直线 是曲线 是曲线 的切线 的切线 |
您最近一年使用:0次
昨日更新
|
43次组卷
|
2卷引用:四川省成都市天府新区太平中学2024届高三数学文科模拟测试(三)
解题方法
4 . 证明幂函数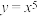 图象关于原点成中心对称.
图象关于原点成中心对称.
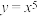 图象关于原点成中心对称.
图象关于原点成中心对称.
您最近一年使用:0次
5 . 已知函数 的定义域为
的定义域为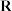 ,且满足
,且满足 ,
, ,当
,当 时,
时,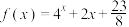 ,则下列结论正确的是( )
,则下列结论正确的是( )
 的定义域为
的定义域为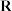 ,且满足
,且满足 ,
, ,当
,当 时,
时,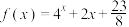 ,则下列结论正确的是( )
,则下列结论正确的是( )A. 为偶函数 为偶函数 |
B. 在 在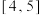 上单调递增 上单调递增 |
C. 关于点 关于点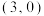 中心对称 中心对称 |
D.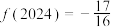 |
您最近一年使用:0次
7日内更新
|
360次组卷
|
2卷引用:山东省德州市2023-2024学年高二下学期7月期末考试数学试题
6 . 定义:若对于任意 ,数列
,数列 满足:①
满足:① ;②
;② ,其中
,其中 的定义域为
的定义域为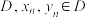 ,则称
,则称 关于
关于 满足性质
满足性质 .
.
(1)请写出一个定义域为 的函数
的函数 ,使得
,使得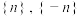 关于
关于 满足性质
满足性质 ;
;
(2)设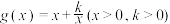 ,若
,若 关于
关于 满足性质
满足性质 ,证明:
,证明: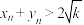 ;
;
(3)设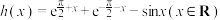 ,若
,若 关于
关于 满足性质
满足性质 ,求数列
,求数列 的前
的前 项和.
项和.
 ,数列
,数列 满足:①
满足:① ;②
;② ,其中
,其中 的定义域为
的定义域为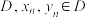 ,则称
,则称 关于
关于 满足性质
满足性质 .
.(1)请写出一个定义域为
 的函数
的函数 ,使得
,使得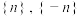 关于
关于 满足性质
满足性质 ;
;(2)设
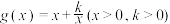 ,若
,若 关于
关于 满足性质
满足性质 ,证明:
,证明: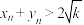 ;
;(3)设
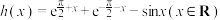 ,若
,若 关于
关于 满足性质
满足性质 ,求数列
,求数列 的前
的前 项和.
项和.
您最近一年使用:0次
名校
7 . 设函数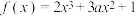 ,则( )
,则( )
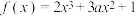 ,则( )
,则( )A.当 时, 时, 有三个零点 有三个零点 |
B.当 时, 时, 是 是 的极大值点 的极大值点 |
C.存在 ,使得 ,使得 为曲线 为曲线 的对称轴 的对称轴 |
D.存在 ,使得点 ,使得点 为曲线 为曲线 的对称中心 的对称中心 |
您最近一年使用:0次
名校
解题方法
8 . 已知定义在R上的函数 满足:
满足: ,若
,若 为数列
为数列 的前n项和,且
的前n项和,且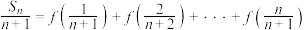 ,(
,( )则下列结论中正确的有( )
)则下列结论中正确的有( )
 满足:
满足: ,若
,若 为数列
为数列 的前n项和,且
的前n项和,且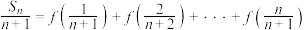 ,(
,( )则下列结论中正确的有( )
)则下列结论中正确的有( )A. | B.数列 为等比数列 为等比数列 |
C. 为等差数列 为等差数列 | D.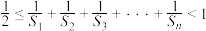 |
您最近一年使用:0次
名校
解题方法
9 . 已知函数 是定义在
是定义在 上的奇函数,
上的奇函数, ,则下列说法正确的是( )
,则下列说法正确的是( )
 是定义在
是定义在 上的奇函数,
上的奇函数, ,则下列说法正确的是( )
,则下列说法正确的是( )A. 的最小正周期为8 的最小正周期为8 | B. 的图象关于直线 的图象关于直线 对称 对称 |
C. 的图象关于点 的图象关于点 对称 对称 | D. 在 在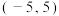 内至少有5个零点 内至少有5个零点 |
您最近一年使用:0次
名校
解题方法
10 . 已知函数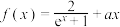 .
.
(1)若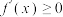 ,求
,求 的最小值;
的最小值;
(2)证明:曲线 是中心对称图形.
是中心对称图形.
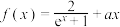 .
.(1)若
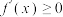 ,求
,求 的最小值;
的最小值;(2)证明:曲线
 是中心对称图形.
是中心对称图形.
您最近一年使用:0次



