1 . 德国著名数学家狄利克雷在数学领域成就显著,以其命名的函数 ,被称为狄利克雷函数,其中
,被称为狄利克雷函数,其中 为实数集,
为实数集, 为有理数集,则以下关于狄利克雷函数
为有理数集,则以下关于狄利克雷函数 的结论中,正确的是( )
的结论中,正确的是( )
 ,被称为狄利克雷函数,其中
,被称为狄利克雷函数,其中 为实数集,
为实数集, 为有理数集,则以下关于狄利克雷函数
为有理数集,则以下关于狄利克雷函数 的结论中,正确的是( )
的结论中,正确的是( )A.函数 满足: 满足: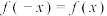 |
B.函数 的值域是 的值域是 |
C.对于任意的 ,都有 ,都有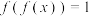 |
D.在 图象上不存在不同的三个点 图象上不存在不同的三个点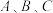 ,使得 ,使得 为等边三角形 为等边三角形 |
您最近一年使用:0次
2 . 设函数 的定义域为
的定义域为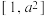 ,其中常数
,其中常数 .若存在常数
.若存在常数 ,使得对任意的
,使得对任意的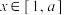 ,都有
,都有 ,则称函数
,则称函数 具有性质
具有性质 .
.
(1)当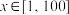 时, 函数
时, 函数 和
和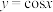 是否具有性质
是否具有性质 ?
?
(2)若 ,函数
,函数 具有性质
具有性质 ,且当
,且当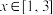 时,
时,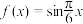 ,求不等式
,求不等式 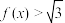 的解集.
的解集.
(3)已知函数 具有性质
具有性质 ,
,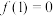 , 且
, 且 的图象是轴对称图形. 若
的图象是轴对称图形. 若 在
在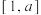 上有最大值
上有最大值 ,且存在
,且存在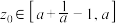 ,使得
,使得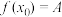 ,求证:
,求证: .
.
 的定义域为
的定义域为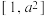 ,其中常数
,其中常数 .若存在常数
.若存在常数 ,使得对任意的
,使得对任意的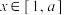 ,都有
,都有 ,则称函数
,则称函数 具有性质
具有性质 .
.(1)当
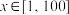 时, 函数
时, 函数 和
和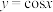 是否具有性质
是否具有性质 ?
?(2)若
 ,函数
,函数 具有性质
具有性质 ,且当
,且当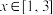 时,
时,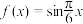 ,求不等式
,求不等式 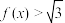 的解集.
的解集.(3)已知函数
 具有性质
具有性质 ,
,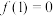 , 且
, 且 的图象是轴对称图形. 若
的图象是轴对称图形. 若 在
在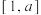 上有最大值
上有最大值 ,且存在
,且存在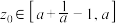 ,使得
,使得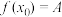 ,求证:
,求证: .
.
您最近一年使用:0次
名校
解题方法
3 . 高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德、牛顿并列为世界三大数学家,用其名字命名的“高斯函数”为:设 ,用
,用 表示不超过
表示不超过 的最大整数,则
的最大整数,则 称为高斯函数,如
称为高斯函数,如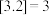 ,
,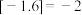 .若
.若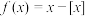 ,
, ,则下列说法正确的是( )
,则下列说法正确的是( )
 ,用
,用 表示不超过
表示不超过 的最大整数,则
的最大整数,则 称为高斯函数,如
称为高斯函数,如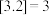 ,
,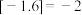 .若
.若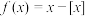 ,
, ,则下列说法正确的是( )
,则下列说法正确的是( )A.当 时, 时,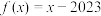 |
B.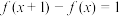 |
C.函数 的值域为 的值域为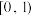 |
D.当 时,函数 时,函数 的值域为 的值域为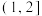 |
您最近一年使用:0次
昨日更新
|
367次组卷
|
2卷引用:黑龙江省大庆铁人中学2024-2025学年高一上学期第一次月考数学试卷
4 . 阅读材料一:设函数 在区间
在区间 上有定义,若对任意
上有定义,若对任意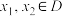 和任意
和任意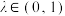 ,都有
,都有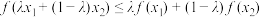 ,则称
,则称 是区间
是区间 上的下凸函数;反之,如果都有
上的下凸函数;反之,如果都有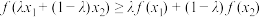 ,则称
,则称 是区间
是区间 上的上凸函数.阅读材料二:若函数
上的上凸函数.阅读材料二:若函数 在区间
在区间 上可导,即
上可导,即 存在,且导函数
存在,且导函数 在区间
在区间 上也可导,则称
上也可导,则称 在区间
在区间 上存在二阶导函数,即
上存在二阶导函数,即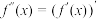 .设函数
.设函数 在区间
在区间 上存在二阶导函数,则
上存在二阶导函数,则 在区间
在区间 上是下凸(上凸)函数的充要条件是对任意
上是下凸(上凸)函数的充要条件是对任意 都有
都有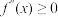 (
(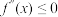 )且在区间
)且在区间 的任意子区间内
的任意子区间内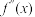 不恒为0.阅读材料三:设函数
不恒为0.阅读材料三:设函数 在区间
在区间 上连续,
上连续,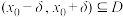 (其中
(其中 为无限接近于0的正数),
为无限接近于0的正数), 在
在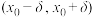 上存在二阶导函数,若
上存在二阶导函数,若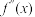 在
在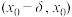 和
和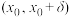 上的符号相反,则点
上的符号相反,则点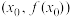 为曲线
为曲线 的拐点.请根据以上阅读材料,回答下列问题:
的拐点.请根据以上阅读材料,回答下列问题:
(1)证明:对任意 ,
, ,不等式
,不等式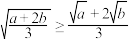 恒成立;
恒成立;
(2)设函数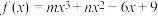 ,若点
,若点 是曲线
是曲线 的拐点,求实数
的拐点,求实数 ,
, 的值,并证明
的值,并证明 的图象关于拐点
的图象关于拐点 中心对称:
中心对称:
(3)设函数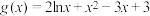 ,若点
,若点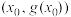 是曲线
是曲线 的一个拐点,且
的一个拐点,且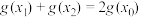 ,其中
,其中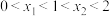 ,试证明:
,试证明: .
.
 在区间
在区间 上有定义,若对任意
上有定义,若对任意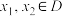 和任意
和任意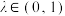 ,都有
,都有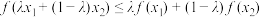 ,则称
,则称 是区间
是区间 上的下凸函数;反之,如果都有
上的下凸函数;反之,如果都有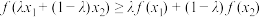 ,则称
,则称 是区间
是区间 上的上凸函数.阅读材料二:若函数
上的上凸函数.阅读材料二:若函数 在区间
在区间 上可导,即
上可导,即 存在,且导函数
存在,且导函数 在区间
在区间 上也可导,则称
上也可导,则称 在区间
在区间 上存在二阶导函数,即
上存在二阶导函数,即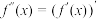 .设函数
.设函数 在区间
在区间 上存在二阶导函数,则
上存在二阶导函数,则 在区间
在区间 上是下凸(上凸)函数的充要条件是对任意
上是下凸(上凸)函数的充要条件是对任意 都有
都有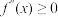 (
(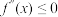 )且在区间
)且在区间 的任意子区间内
的任意子区间内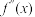 不恒为0.阅读材料三:设函数
不恒为0.阅读材料三:设函数 在区间
在区间 上连续,
上连续,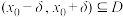 (其中
(其中 为无限接近于0的正数),
为无限接近于0的正数), 在
在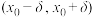 上存在二阶导函数,若
上存在二阶导函数,若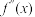 在
在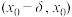 和
和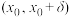 上的符号相反,则点
上的符号相反,则点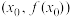 为曲线
为曲线 的拐点.请根据以上阅读材料,回答下列问题:
的拐点.请根据以上阅读材料,回答下列问题:(1)证明:对任意
 ,
, ,不等式
,不等式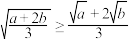 恒成立;
恒成立;(2)设函数
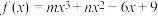 ,若点
,若点 是曲线
是曲线 的拐点,求实数
的拐点,求实数 ,
, 的值,并证明
的值,并证明 的图象关于拐点
的图象关于拐点 中心对称:
中心对称:(3)设函数
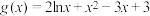 ,若点
,若点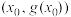 是曲线
是曲线 的一个拐点,且
的一个拐点,且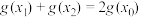 ,其中
,其中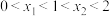 ,试证明:
,试证明: .
.
您最近一年使用:0次
名校
5 . 对于集合M,定义函数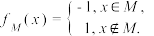 对于两个集合
对于两个集合 ,定义集合
,定义集合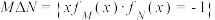 .已知
.已知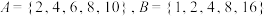
(1)写出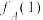 和
和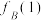 的值,并用列举法写出集合
的值,并用列举法写出集合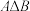 ;
;
(2)用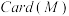 表示有限集合M所含元素的个数,求
表示有限集合M所含元素的个数,求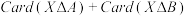 的最小值;
的最小值;
(3)有多少个集合对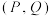 ,满足
,满足 ,
, ,且
,且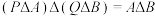 ?
?
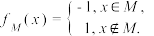 对于两个集合
对于两个集合 ,定义集合
,定义集合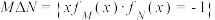 .已知
.已知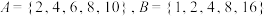
(1)写出
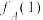 和
和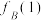 的值,并用列举法写出集合
的值,并用列举法写出集合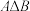 ;
;(2)用
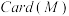 表示有限集合M所含元素的个数,求
表示有限集合M所含元素的个数,求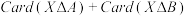 的最小值;
的最小值;(3)有多少个集合对
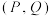 ,满足
,满足 ,
, ,且
,且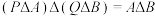 ?
?
您最近一年使用:0次
名校
6 .  表示不超过
表示不超过 的最大整数,例如,
的最大整数,例如, ,
,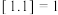 ,已知函数
,已知函数 ,下列结论正确的有( )
,下列结论正确的有( )
 表示不超过
表示不超过 的最大整数,例如,
的最大整数,例如, ,
,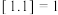 ,已知函数
,已知函数 ,下列结论正确的有( )
,下列结论正确的有( )A.若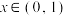 ,则 ,则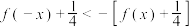 |
B.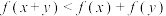 |
C.设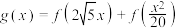 ,则 ,则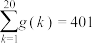 |
D.所有满足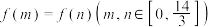 的点 的点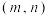 组成的区域的面积和为 组成的区域的面积和为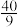 |
您最近一年使用:0次
名校
解题方法
7 . 对于函数 ,如果对于其定义域D中任意给定的实数x,都有
,如果对于其定义域D中任意给定的实数x,都有 ,并且
,并且 ,则称函数
,则称函数 为“倒函数”.则下列说法正确的是( )
为“倒函数”.则下列说法正确的是( )
 ,如果对于其定义域D中任意给定的实数x,都有
,如果对于其定义域D中任意给定的实数x,都有 ,并且
,并且 ,则称函数
,则称函数 为“倒函数”.则下列说法正确的是( )
为“倒函数”.则下列说法正确的是( )A.函数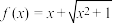 是“倒函数” 是“倒函数” |
B.若函数 在R上为“倒函数”,则 在R上为“倒函数”,则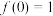 |
C.若函数 在R上为“倒函数”,当 在R上为“倒函数”,当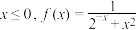 ,则 ,则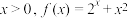 |
D.若函数 在R上为“倒函数”,其函数值恒大于0,且在R上是单调增函数,记 在R上为“倒函数”,其函数值恒大于0,且在R上是单调增函数,记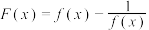 ,若 ,若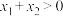 ,则 ,则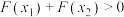 . . |
您最近一年使用:0次
名校
解题方法
8 . 已知定义域为 的函数
的函数 ,若存在正数
,若存在正数 ,对任意
,对任意 ,都有
,都有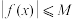 成立,则称函数
成立,则称函数 是定义域
是定义域 上的有界函数.下列选项中是有界函数的是( )
上的有界函数.下列选项中是有界函数的是( )
 的函数
的函数 ,若存在正数
,若存在正数 ,对任意
,对任意 ,都有
,都有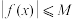 成立,则称函数
成立,则称函数 是定义域
是定义域 上的有界函数.下列选项中是有界函数的是( )
上的有界函数.下列选项中是有界函数的是( )A.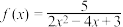 | B. | C.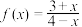 | D.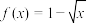 |
您最近一年使用:0次
名校
9 . 现定义 表示不超过实数x的最大整数,如
表示不超过实数x的最大整数,如 
(1)求不等式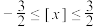 的解集:
的解集:
(2)求不等式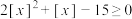 的解集:
的解集:
(3)若对任意的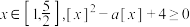 恒成立,求a的取值范围:
恒成立,求a的取值范围:
(4)若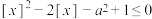 的解集为
的解集为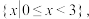 求a的取值范围.
求a的取值范围.
 表示不超过实数x的最大整数,如
表示不超过实数x的最大整数,如 
(1)求不等式
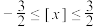 的解集:
的解集:(2)求不等式
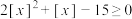 的解集:
的解集:(3)若对任意的
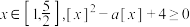 恒成立,求a的取值范围:
恒成立,求a的取值范围:(4)若
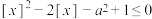 的解集为
的解集为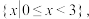 求a的取值范围.
求a的取值范围.
您最近一年使用:0次
10 . 已知函数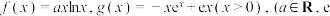 为自然对数的底数
为自然对数的底数 ,
,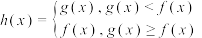 ,曲线
,曲线 与
与 在
在 处的切线的倾斜角互补.
处的切线的倾斜角互补.
(1)求 的值;
的值;
(2)求 的单调递增区间;
的单调递增区间;
(3)若存在实常数 和
和 ,使得函数
,使得函数 和
和 对其公共定义域上的任意实数
对其公共定义域上的任意实数 都满足
都满足 和
和 恒成立,则称直线
恒成立,则称直线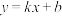 为函数
为函数 和
和 的“隔离直线”.证明:函数
的“隔离直线”.证明:函数 和
和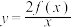 之间存在唯一的“隔离直线”.
之间存在唯一的“隔离直线”.
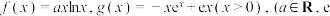 为自然对数的底数
为自然对数的底数 ,
,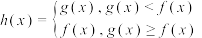 ,曲线
,曲线 与
与 在
在 处的切线的倾斜角互补.
处的切线的倾斜角互补.(1)求
 的值;
的值;(2)求
 的单调递增区间;
的单调递增区间;(3)若存在实常数
 和
和 ,使得函数
,使得函数 和
和 对其公共定义域上的任意实数
对其公共定义域上的任意实数 都满足
都满足 和
和 恒成立,则称直线
恒成立,则称直线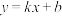 为函数
为函数 和
和 的“隔离直线”.证明:函数
的“隔离直线”.证明:函数 和
和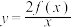 之间存在唯一的“隔离直线”.
之间存在唯一的“隔离直线”.
您最近一年使用:0次



