1 . 已知函数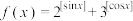 ,其中
,其中 表示不超过
表示不超过 的最大整数.如:
的最大整数.如: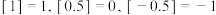 ,以下三个结论:
,以下三个结论:
①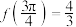 ;
;
②集合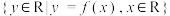 的元素个数为9;
的元素个数为9;
③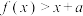 对任意
对任意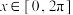 都成立,则实数
都成立,则实数 的取值范围是
的取值范围是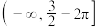 .
.
其中所有正确结论的序号是___ .
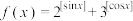 ,其中
,其中 表示不超过
表示不超过 的最大整数.如:
的最大整数.如: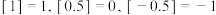 ,以下三个结论:
,以下三个结论:①
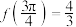 ;
;②集合
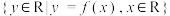 的元素个数为9;
的元素个数为9;③
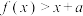 对任意
对任意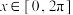 都成立,则实数
都成立,则实数 的取值范围是
的取值范围是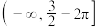 .
.其中所有正确结论的序号是
您最近一年使用:0次
2 . 如图所示,角 (
( )的顶点为坐标原点,始边与
)的顶点为坐标原点,始边与 轴的非负半轴重合,其终边与单位圆的交点为
轴的非负半轴重合,其终边与单位圆的交点为 ,分别过点
,分别过点 作
作 轴的垂线,过点
轴的垂线,过点 作
作 轴的垂线交角
轴的垂线交角 的终边于
的终边于 ,
, ,根据三角函数的定义,
,根据三角函数的定义,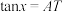 .现在定义余切函数
.现在定义余切函数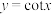 ,满足
,满足 ,则下列表示正确的是( )
,则下列表示正确的是( )
 (
( )的顶点为坐标原点,始边与
)的顶点为坐标原点,始边与 轴的非负半轴重合,其终边与单位圆的交点为
轴的非负半轴重合,其终边与单位圆的交点为 ,分别过点
,分别过点 作
作 轴的垂线,过点
轴的垂线,过点 作
作 轴的垂线交角
轴的垂线交角 的终边于
的终边于 ,
, ,根据三角函数的定义,
,根据三角函数的定义,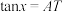 .现在定义余切函数
.现在定义余切函数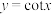 ,满足
,满足 ,则下列表示正确的是( )
,则下列表示正确的是( )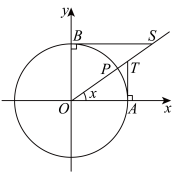
A. | B.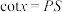 | C.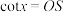 | D.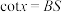 |
您最近一年使用:0次
名校
解题方法
3 . 对于定义在R上的连续函数 ,若存在常数t(
,若存在常数t(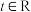 ),使得
),使得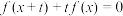 对任意的实数x都成立,则称
对任意的实数x都成立,则称 是阶数为t的回旋函数.
是阶数为t的回旋函数.
(1)试判断函数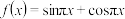 是否是一个阶数为
是否是一个阶数为 的回旋函数,并说明理由;
的回旋函数,并说明理由;
(2)若 是回旋函数,求实数ω的值;
是回旋函数,求实数ω的值;
(3)若回旋函数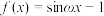 (
( )在[0,1]上恰有2024个零点,求ω的值.
)在[0,1]上恰有2024个零点,求ω的值.
 ,若存在常数t(
,若存在常数t(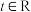 ),使得
),使得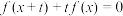 对任意的实数x都成立,则称
对任意的实数x都成立,则称 是阶数为t的回旋函数.
是阶数为t的回旋函数.(1)试判断函数
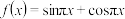 是否是一个阶数为
是否是一个阶数为 的回旋函数,并说明理由;
的回旋函数,并说明理由;(2)若
 是回旋函数,求实数ω的值;
是回旋函数,求实数ω的值;(3)若回旋函数
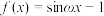 (
( )在[0,1]上恰有2024个零点,求ω的值.
)在[0,1]上恰有2024个零点,求ω的值.
您最近一年使用:0次
2024-07-13更新
|
239次组卷
|
2卷引用:河南省九师联盟2023-2024学年高一下学期6月份质量检测数学试卷
4 . 在三角函数领域,为了三角计算的简便并且追求计算的精确性,曾经出现过以下两种少见的三角函数:定义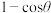 为角
为角 的正矢(
的正矢(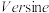 或
或 ),记作
),记作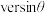 ;定义
;定义 为角
为角 的余矢(Coversed或coversedsine),记作
的余矢(Coversed或coversedsine),记作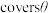 .
.
(1)设函数 ,求函数
,求函数 的单调递减区间;
的单调递减区间;
(2)当 时,设函数
时,设函数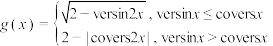 ,若关于
,若关于 的方程
的方程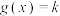 的有三个实根
的有三个实根 ,则:
,则:
①求实数 的取值范围;
的取值范围;
②求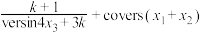 的取值范围.
的取值范围.
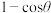 为角
为角 的正矢(
的正矢(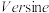 或
或 ),记作
),记作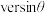 ;定义
;定义 为角
为角 的余矢(Coversed或coversedsine),记作
的余矢(Coversed或coversedsine),记作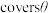 .
.(1)设函数
 ,求函数
,求函数 的单调递减区间;
的单调递减区间;(2)当
 时,设函数
时,设函数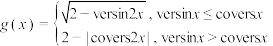 ,若关于
,若关于 的方程
的方程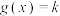 的有三个实根
的有三个实根 ,则:
,则:①求实数
 的取值范围;
的取值范围;②求
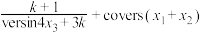 的取值范围.
的取值范围.
您最近一年使用:0次
23-24高一下·贵州贵阳·期末
名校
解题方法
5 . 人脸识别就是利用计算机检测样本之间的相似度,余弦距离是检测相似度的常用方法.假设二维空间中有两个点 ,
, ,O为坐标原点,定义余弦相似度为
,O为坐标原点,定义余弦相似度为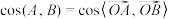 ,余弦距离为
,余弦距离为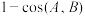 .已知
.已知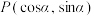 ,
, ,若P,Q的余弦距离为
,若P,Q的余弦距离为 .则
.则 ( )
( )
 ,
, ,O为坐标原点,定义余弦相似度为
,O为坐标原点,定义余弦相似度为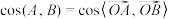 ,余弦距离为
,余弦距离为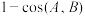 .已知
.已知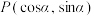 ,
, ,若P,Q的余弦距离为
,若P,Q的余弦距离为 .则
.则 ( )
( )A. | B. | C. | D. |
您最近一年使用:0次
2024-06-21更新
|
295次组卷
|
5卷引用:贵州省贵阳市南明区部分学校2023-2024学年高一下学期6月联考数学试题
(已下线)贵州省贵阳市南明区部分学校2023-2024学年高一下学期6月联考数学试题广东省部分学校2023-2024学年高一下学期期末联考数学试题贵州省遵义市2023-2024学年高一下学期5月期中数学试题辽宁省大连市育明高中2023-2024学年高一下学期期末考试数学试卷贵州省贵阳市南明区部分学校2023-2024学年高一下学期6月联考数学试卷
名校
解题方法
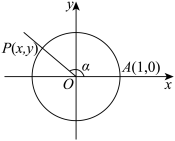
6 . 一般地,任意给定一个角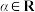 ,它的终边
,它的终边 与单位圆的交点
与单位圆的交点 的坐标,无论是横坐标
的坐标,无论是横坐标 还是纵坐标
还是纵坐标 ,都是唯一确定的,所以点
,都是唯一确定的,所以点 的横坐标
的横坐标 、纵坐标
、纵坐标 都是关于角
都是关于角 的函数.下面给出这些函数的定义:
的函数.下面给出这些函数的定义:
①把点 的纵坐标
的纵坐标 叫作
叫作 的正弦函数,记作
的正弦函数,记作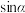 ,即
,即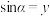 ;
;
②把点 的横坐标
的横坐标 叫作
叫作 的余弦函数,记作
的余弦函数,记作 ,即
,即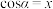 ;
;
③把点 的纵坐标
的纵坐标 的倒数叫作
的倒数叫作 的余割函数,记作
的余割函数,记作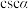 ,即
,即 ;
;
④把点 的横坐标
的横坐标 的倒数叫作
的倒数叫作 的正割函数,记作
的正割函数,记作 ,即
,即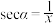 .
.
下列结论错误的是( )
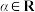 ,它的终边
,它的终边 与单位圆的交点
与单位圆的交点 的坐标,无论是横坐标
的坐标,无论是横坐标 还是纵坐标
还是纵坐标 ,都是唯一确定的,所以点
,都是唯一确定的,所以点 的横坐标
的横坐标 、纵坐标
、纵坐标 都是关于角
都是关于角 的函数.下面给出这些函数的定义:
的函数.下面给出这些函数的定义:①把点
 的纵坐标
的纵坐标 叫作
叫作 的正弦函数,记作
的正弦函数,记作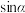 ,即
,即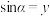 ;
;②把点
 的横坐标
的横坐标 叫作
叫作 的余弦函数,记作
的余弦函数,记作 ,即
,即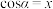 ;
;③把点
 的纵坐标
的纵坐标 的倒数叫作
的倒数叫作 的余割函数,记作
的余割函数,记作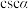 ,即
,即 ;
;④把点
 的横坐标
的横坐标 的倒数叫作
的倒数叫作 的正割函数,记作
的正割函数,记作 ,即
,即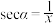 .
.下列结论错误的是( )
A.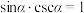 |
B.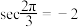 |
C.函数 的定义域为 的定义域为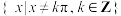 |
D.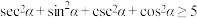 |
您最近一年使用:0次
7 . 密位制是度量角的一种方法.把一周角等分为 份,每一份叫做1密位的角.以密位作为角的度量单位,这种度量角的单位制,叫做角的密位制.在角的密位制中,采用四个数码表示角的大小,单位名称密位二字可以省去不写.密位的写法是在百位数与十位数字之间画一条短线,如7密位写成“
份,每一份叫做1密位的角.以密位作为角的度量单位,这种度量角的单位制,叫做角的密位制.在角的密位制中,采用四个数码表示角的大小,单位名称密位二字可以省去不写.密位的写法是在百位数与十位数字之间画一条短线,如7密位写成“ ”,
”,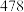 密位写成“
密位写成“ ”.1周角等于
”.1周角等于 密位,记作1周角
密位,记作1周角 ,1直角
,1直角 .如果一个半径为
.如果一个半径为 的扇形,它的面积为
的扇形,它的面积为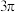 ,则其圆心角用密位制表示为( )
,则其圆心角用密位制表示为( )
 份,每一份叫做1密位的角.以密位作为角的度量单位,这种度量角的单位制,叫做角的密位制.在角的密位制中,采用四个数码表示角的大小,单位名称密位二字可以省去不写.密位的写法是在百位数与十位数字之间画一条短线,如7密位写成“
份,每一份叫做1密位的角.以密位作为角的度量单位,这种度量角的单位制,叫做角的密位制.在角的密位制中,采用四个数码表示角的大小,单位名称密位二字可以省去不写.密位的写法是在百位数与十位数字之间画一条短线,如7密位写成“ ”,
”,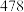 密位写成“
密位写成“ ”.1周角等于
”.1周角等于 密位,记作1周角
密位,记作1周角 ,1直角
,1直角 .如果一个半径为
.如果一个半径为 的扇形,它的面积为
的扇形,它的面积为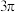 ,则其圆心角用密位制表示为( )
,则其圆心角用密位制表示为( )A. | B. | C. | D. |
您最近一年使用:0次
2024-05-27更新
|
415次组卷
|
4卷引用:重庆市西南大学附属中学校2023-2024学年高一下学期定时检测(二)(期中)数学试题
重庆市西南大学附属中学校2023-2024学年高一下学期定时检测(二)(期中)数学试题浙江省杭州学军中学2023-2024学年高一下学期统测适应性考试数学试卷(已下线)任意角和弧度制、三角函数的概念-一轮复习考点专练广西北海市2023-2024学年高一下学期期末教学质量检测数学试卷
8 . 对于定义域为R的函数 ,若存在常数
,若存在常数 ,使得
,使得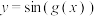 是以
是以 为周期的周期函数,则称
为周期的周期函数,则称 为“正弦周期函数”,且称
为“正弦周期函数”,且称 为其“正弦周期”.
为其“正弦周期”.
(1)判断函数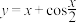 是否为“正弦周期函数”,并说明理由;
是否为“正弦周期函数”,并说明理由;
(2)已知 是定义在R上的严格增函数,值域为R,且
是定义在R上的严格增函数,值域为R,且 是以
是以 为“正弦周期”的“正弦周期函数”,若
为“正弦周期”的“正弦周期函数”,若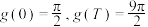 ,且存在
,且存在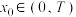 ,使得
,使得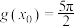 ,求
,求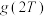 的值;
的值;
(3)已知 是以
是以 为一个“正弦周期”的“正弦周期函数”,且存在
为一个“正弦周期”的“正弦周期函数”,且存在 和
和 ,使得对任意
,使得对任意 ,都有
,都有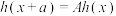 ,证明:
,证明: 是周期函数.
是周期函数.
 ,若存在常数
,若存在常数 ,使得
,使得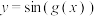 是以
是以 为周期的周期函数,则称
为周期的周期函数,则称 为“正弦周期函数”,且称
为“正弦周期函数”,且称 为其“正弦周期”.
为其“正弦周期”.(1)判断函数
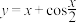 是否为“正弦周期函数”,并说明理由;
是否为“正弦周期函数”,并说明理由;(2)已知
 是定义在R上的严格增函数,值域为R,且
是定义在R上的严格增函数,值域为R,且 是以
是以 为“正弦周期”的“正弦周期函数”,若
为“正弦周期”的“正弦周期函数”,若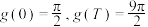 ,且存在
,且存在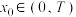 ,使得
,使得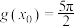 ,求
,求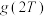 的值;
的值;(3)已知
 是以
是以 为一个“正弦周期”的“正弦周期函数”,且存在
为一个“正弦周期”的“正弦周期函数”,且存在 和
和 ,使得对任意
,使得对任意 ,都有
,都有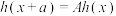 ,证明:
,证明: 是周期函数.
是周期函数.
您最近一年使用:0次
9 . 点 将一条线段
将一条线段 分为两段
分为两段 和
和 ,若
,若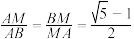 ,则称点
,则称点 为线段
为线段 的黄金分割点.已知直线
的黄金分割点.已知直线 与函数
与函数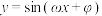 的图象相交,
的图象相交, 为相邻的三个交点,则( )
为相邻的三个交点,则( )
 将一条线段
将一条线段 分为两段
分为两段 和
和 ,若
,若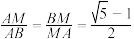 ,则称点
,则称点 为线段
为线段 的黄金分割点.已知直线
的黄金分割点.已知直线 与函数
与函数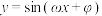 的图象相交,
的图象相交, 为相邻的三个交点,则( )
为相邻的三个交点,则( )A.当 时,存在 时,存在 使点 使点 为线段 为线段 的黄金分割点 的黄金分割点 |
B.对于给定的常数 ,不存在 ,不存在 使点 使点 为线段 为线段 的黄金分割点 的黄金分割点 |
C.对于任意的 ,存在 ,存在 使点 使点 为线段 为线段 的黄金分割点 的黄金分割点 |
D.对于任意的 ,存在 ,存在 使点 使点 为线段 为线段 的黄金分割点 的黄金分割点 |
您最近一年使用:0次
2024-05-18更新
|
197次组卷
|
2卷引用:江西省萍乡市2024届高三二模考试数学试卷
名校
解题方法
10 . 已知在平面直角坐标系中,O为坐标原点,定义函数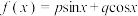 的“和谐向量”为非零向量
的“和谐向量”为非零向量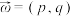 ,
,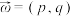 的“和谐函数”为
的“和谐函数”为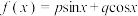 .记平面内所有向量的“和谐函数”构成的集合为T.
.记平面内所有向量的“和谐函数”构成的集合为T.
(1)已知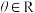 ,
, ,若函数
,若函数 为集合T中的元素,求其“和谐向量”模的取值范围;
为集合T中的元素,求其“和谐向量”模的取值范围;
(2)已知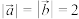 ,设
,设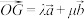 (
( ,
, ),且
),且 的“和谐函数”为
的“和谐函数”为 ,其最大值为S,求
,其最大值为S,求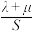 .
.
(3)已知 ,
,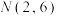 ,设(1)中的“和谐函数”的模取得最小时的“和谐函数”为
,设(1)中的“和谐函数”的模取得最小时的“和谐函数”为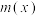 ,
,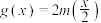 ,试问在
,试问在 的图象上是否存在一点Q,使得
的图象上是否存在一点Q,使得 ,若存在,求出Q点坐标;若不存在,说明理由.
,若存在,求出Q点坐标;若不存在,说明理由.
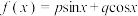 的“和谐向量”为非零向量
的“和谐向量”为非零向量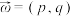 ,
,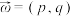 的“和谐函数”为
的“和谐函数”为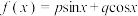 .记平面内所有向量的“和谐函数”构成的集合为T.
.记平面内所有向量的“和谐函数”构成的集合为T.(1)已知
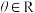 ,
, ,若函数
,若函数 为集合T中的元素,求其“和谐向量”模的取值范围;
为集合T中的元素,求其“和谐向量”模的取值范围;(2)已知
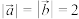 ,设
,设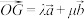 (
( ,
, ),且
),且 的“和谐函数”为
的“和谐函数”为 ,其最大值为S,求
,其最大值为S,求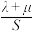 .
.(3)已知
 ,
,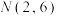 ,设(1)中的“和谐函数”的模取得最小时的“和谐函数”为
,设(1)中的“和谐函数”的模取得最小时的“和谐函数”为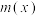 ,
,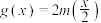 ,试问在
,试问在 的图象上是否存在一点Q,使得
的图象上是否存在一点Q,使得 ,若存在,求出Q点坐标;若不存在,说明理由.
,若存在,求出Q点坐标;若不存在,说明理由.
您最近一年使用:0次



