名校
1 . 已知 在定义域
在定义域 上是连续不断的函数,对于区间
上是连续不断的函数,对于区间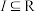 若存在
若存在 ,使得对任意的
,使得对任意的 ,都有
,都有 ,则称
,则称 在区间
在区间 上存在最大值
上存在最大值 .
.
(1)函数 在区间
在区间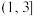 存在最大值,求实数m的取值范围;
存在最大值,求实数m的取值范围;
(2)若函数 为奇函数,在
为奇函数,在 上,
上, ,易证对任意
,易证对任意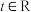 ,函数
,函数 在区间
在区间 上存在最大值M,试写出最大值M关于t的函数关系式
上存在最大值M,试写出最大值M关于t的函数关系式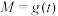 ;
;
(3)若对任意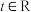 ,函数
,函数 在区间
在区间 上存在最大值M,设最大值M关于t的函数关系式为
上存在最大值M,设最大值M关于t的函数关系式为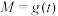 ,求证:“
,求证:“ 在定义域
在定义域 上是严格增函数”的充要条件是“
上是严格增函数”的充要条件是“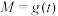 在定义域
在定义域 上是严格增函数”.
上是严格增函数”.
 在定义域
在定义域 上是连续不断的函数,对于区间
上是连续不断的函数,对于区间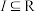 若存在
若存在 ,使得对任意的
,使得对任意的 ,都有
,都有 ,则称
,则称 在区间
在区间 上存在最大值
上存在最大值 .
.(1)函数
 在区间
在区间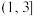 存在最大值,求实数m的取值范围;
存在最大值,求实数m的取值范围;(2)若函数
 为奇函数,在
为奇函数,在 上,
上, ,易证对任意
,易证对任意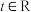 ,函数
,函数 在区间
在区间 上存在最大值M,试写出最大值M关于t的函数关系式
上存在最大值M,试写出最大值M关于t的函数关系式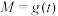 ;
;(3)若对任意
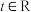 ,函数
,函数 在区间
在区间 上存在最大值M,设最大值M关于t的函数关系式为
上存在最大值M,设最大值M关于t的函数关系式为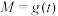 ,求证:“
,求证:“ 在定义域
在定义域 上是严格增函数”的充要条件是“
上是严格增函数”的充要条件是“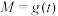 在定义域
在定义域 上是严格增函数”.
上是严格增函数”.
您最近一年使用:0次
2023-12-01更新
|
92次组卷
|
5卷引用:上海市格致中学2021-2022学年高一上学期12月月考数学试题
上海市格致中学2021-2022学年高一上学期12月月考数学试题(已下线)第5章 函数的概念、性质及应用(基础、典型、易错、压轴)分项训练-2022-2023学年高一数学考试满分全攻略(沪教版2020必修一)(已下线)第五章 函数的概念、性质及应用(压轴必刷30题9种题型专项训练)-【满分全攻略】(沪教版2020必修第一册)(已下线)单元高难问题03函数恒成立问题和存在性问题-【倍速学习法】(沪教版2020必修第一册)(已下线)专题05 二次函数(练习)-2
名校
解题方法
2 . 若函数 的定义域为
的定义域为 ,集合
,集合 ,若存在非零实数
,若存在非零实数 使得任意
使得任意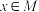 都有
都有 ,且
,且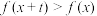 ,则称
,则称 为
为 上的
上的 -增长函数.
-增长函数.
(1)已知函数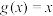 ,函数
,函数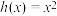 ,判断
,判断 和
和 是否为区间
是否为区间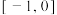 上的
上的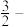 增长函数,并说明理由;
增长函数,并说明理由;
(2)已知函数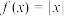 ,且
,且 是区间
是区间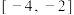 上的
上的 -增长函数,求正整数
-增长函数,求正整数 的最小值;
的最小值;
(3)如果 是定义域为
是定义域为 的奇函数,当
的奇函数,当 时,
时,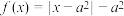 ,且
,且 为
为 上的
上的 增长函数,求实数
增长函数,求实数 的取值范围.
的取值范围.
 的定义域为
的定义域为 ,集合
,集合 ,若存在非零实数
,若存在非零实数 使得任意
使得任意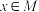 都有
都有 ,且
,且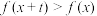 ,则称
,则称 为
为 上的
上的 -增长函数.
-增长函数.(1)已知函数
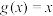 ,函数
,函数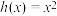 ,判断
,判断 和
和 是否为区间
是否为区间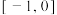 上的
上的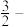 增长函数,并说明理由;
增长函数,并说明理由;(2)已知函数
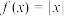 ,且
,且 是区间
是区间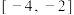 上的
上的 -增长函数,求正整数
-增长函数,求正整数 的最小值;
的最小值;(3)如果
 是定义域为
是定义域为 的奇函数,当
的奇函数,当 时,
时,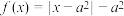 ,且
,且 为
为 上的
上的 增长函数,求实数
增长函数,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2021-01-15更新
|
780次组卷
|
4卷引用:上海市杨浦区控江中学2020-2021学年高一上学期期末数学试题
上海市杨浦区控江中学2020-2021学年高一上学期期末数学试题四川省雅安市2021-2022学年高一上学期期末数学试题福建省厦门双十中学2022-2023常年高一上学期期中考试数学试题(已下线)第3章 函数概念与性质(基础、典型、新文化、易错、压轴)专项训练-2022-2023学年高一数学考试满分全攻略(人教A版2019必修第一册)



