解题方法
1 . 已知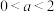 ,函数
,函数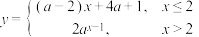 ,若该函数存在最小值,则实数
,若该函数存在最小值,则实数 的取值范围是
的取值范围是______ .
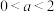 ,函数
,函数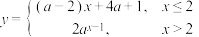 ,若该函数存在最小值,则实数
,若该函数存在最小值,则实数 的取值范围是
的取值范围是
您最近半年使用:0次
名校
解题方法
2 . 已知函数 ,其中
,其中 .
.
(1)当 时,求
时,求 的最小值;
的最小值;
(2)证明 有且仅有一个极小值点
有且仅有一个极小值点 ,并求
,并求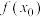 的最大值.
的最大值.
 ,其中
,其中 .
.(1)当
 时,求
时,求 的最小值;
的最小值;(2)证明
 有且仅有一个极小值点
有且仅有一个极小值点 ,并求
,并求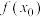 的最大值.
的最大值.
您最近半年使用:0次
23-24高二下·全国·课前预习
3 . 知识点一 函数最值的定义
1、一般地,如果在区间[a,b]上函数y=f(x)的图象是一条_____ 的曲线,那么它必有最大值和最小值.
2、对于函数f(x),给定区间I,若对任意x∈I,存在x0∈I,使得f(x)_____ f(x0),则称f(x0)为函数f(x)在区间I上的最小值;若对任意x∈I,存在x0∈I,使得f(x) _____ f(x0),则称f(x0)为函数f(x)在区间I上的最大值.
1、一般地,如果在区间[a,b]上函数y=f(x)的图象是一条
2、对于函数f(x),给定区间I,若对任意x∈I,存在x0∈I,使得f(x)
您最近半年使用:0次
名校
4 . 已知函数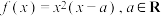 ,且
,且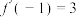 .
.
(1)求 的值及曲线
的值及曲线 在点
在点 处的切线方程;
处的切线方程;
(2)求函数 在区间
在区间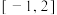 上的最值.
上的最值.
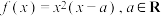 ,且
,且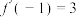 .
.(1)求
 的值及曲线
的值及曲线 在点
在点 处的切线方程;
处的切线方程;(2)求函数
 在区间
在区间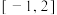 上的最值.
上的最值.
您最近半年使用:0次
名校
5 . 如图,在边长为1的正三角形ABC中,O为中心,过点O的直线交边AB与点M,交边AC于点N, 内部一点(不包括边界),求
内部一点(不包括边界),求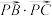 的取值范围;
的取值范围;
(2)若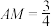 ,求AN的值;
,求AN的值;
(3)求 的最大值与最小值.
的最大值与最小值.
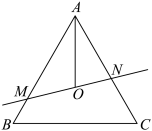
 内部一点(不包括边界),求
内部一点(不包括边界),求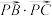 的取值范围;
的取值范围;(2)若
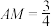 ,求AN的值;
,求AN的值;(3)求
 的最大值与最小值.
的最大值与最小值.
您最近半年使用:0次
解题方法
6 . 已知函数 .
.
(1)判断并证明函数 在
在 上的单调性;
上的单调性;
(2)若存在 ,
,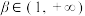 ,使得函数
,使得函数 在区间
在区间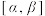 上的值域为
上的值域为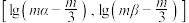 ,求实数
,求实数 的取值范围.
的取值范围.
 .
.(1)判断并证明函数
 在
在 上的单调性;
上的单调性;(2)若存在
 ,
,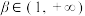 ,使得函数
,使得函数 在区间
在区间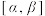 上的值域为
上的值域为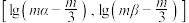 ,求实数
,求实数 的取值范围.
的取值范围.
您最近半年使用:0次
名校
解题方法
7 . 某个体户计划同时销售A,B两种商品,当投资额为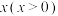 千元时,在销售A,B商品中所获收益分别为
千元时,在销售A,B商品中所获收益分别为 千元与
千元与 千元,其中
千元,其中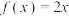 ,
,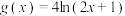 ,如果该个体户准备共投入5千元销售A,B两种商品,为使总收益最大,则B商品需投( )千元.
,如果该个体户准备共投入5千元销售A,B两种商品,为使总收益最大,则B商品需投( )千元.
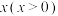 千元时,在销售A,B商品中所获收益分别为
千元时,在销售A,B商品中所获收益分别为 千元与
千元与 千元,其中
千元,其中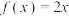 ,
,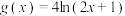 ,如果该个体户准备共投入5千元销售A,B两种商品,为使总收益最大,则B商品需投( )千元.
,如果该个体户准备共投入5千元销售A,B两种商品,为使总收益最大,则B商品需投( )千元.A. | B. | C. | D. |
您最近半年使用:0次
名校
解题方法
8 . 已知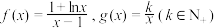 ,对任意的
,对任意的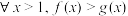 恒成立,则k的最大值为( )
恒成立,则k的最大值为( )
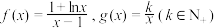 ,对任意的
,对任意的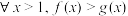 恒成立,则k的最大值为( )
恒成立,则k的最大值为( )| A.2 | B.3 | C.4 | D.5 |
您最近半年使用:0次
名校
9 . 已知集合 ,
,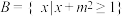 .若“
.若“ ”是“
”是“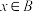 ”的充分不必要条件,则实数m的取值范围为
”的充分不必要条件,则实数m的取值范围为________ .
 ,
,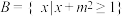 .若“
.若“ ”是“
”是“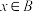 ”的充分不必要条件,则实数m的取值范围为
”的充分不必要条件,则实数m的取值范围为
您最近半年使用:0次
10 . 对任意闭区间I,用 表示函数
表示函数 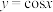 在I上的最大值,若正实数 a 满足
在I上的最大值,若正实数 a 满足  ,则a的值为
,则a的值为 ________ .
 表示函数
表示函数 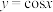 在I上的最大值,若正实数 a 满足
在I上的最大值,若正实数 a 满足  ,则a的值为
,则a的值为
您最近半年使用:0次



