1 . 以下数表构造思路源于我国南宋数学家杨辉所著的《详解九章算法》一书中的“杨辉三角形”.
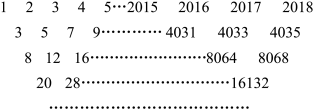
该表由若干行数字组成,从第二行起,第一行中的数字均等于其“肩上”两数之和,表中最后行仅有一个数,则这个数为( )
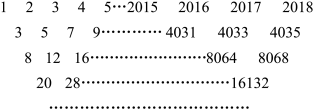
该表由若干行数字组成,从第二行起,第一行中的数字均等于其“肩上”两数之和,表中最后行仅有一个数,则这个数为( )
A.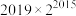 | B.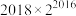 | C. | D.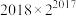 |
您最近一年使用:0次
名校
2 . 欧拉公式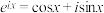 (
( 为虚数单位)是由瑞士著名数学家欧拉发明的,他将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里占有非常重要的地位,被誉为“数学中的天桥”.根据欧拉公式可知,
为虚数单位)是由瑞士著名数学家欧拉发明的,他将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里占有非常重要的地位,被誉为“数学中的天桥”.根据欧拉公式可知,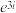 表示的复数在复平面中位于
表示的复数在复平面中位于
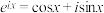 (
( 为虚数单位)是由瑞士著名数学家欧拉发明的,他将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里占有非常重要的地位,被誉为“数学中的天桥”.根据欧拉公式可知,
为虚数单位)是由瑞士著名数学家欧拉发明的,他将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里占有非常重要的地位,被誉为“数学中的天桥”.根据欧拉公式可知,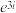 表示的复数在复平面中位于
表示的复数在复平面中位于| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
您最近一年使用:0次
2020-04-30更新
|
802次组卷
|
8卷引用:安徽省黄山市2020-2021学年高三上学期第一次质量检测理科数学试题
3 . 我国古代的“割圆术”相当于给出已知圆的半径 ,计算其面积
,计算其面积 的近似值,进一步计算圆周率的近似值.根据
的近似值,进一步计算圆周率的近似值.根据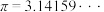 判断,下列近似公式中最接近
判断,下列近似公式中最接近 的是( )
的是( )
 ,计算其面积
,计算其面积 的近似值,进一步计算圆周率的近似值.根据
的近似值,进一步计算圆周率的近似值.根据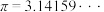 判断,下列近似公式中最接近
判断,下列近似公式中最接近 的是( )
的是( )A. | B. | C.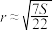 | D.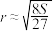 |
您最近一年使用:0次
2020-04-29更新
|
136次组卷
|
2卷引用:2019届安徽省示范联盟高三下学期5月大联考文科数学试题
4 . 我国南北朝数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法,其理论依据是;设实数x的不足近似值和过剩近似值分别为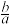 和
和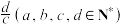 ,则
,则 是x的更为精确的不足近似值或过剩近似值我们知道
是x的更为精确的不足近似值或过剩近似值我们知道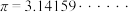 ,若令
,若令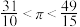 ,则第一次用“调日法”后得
,则第一次用“调日法”后得 是
是 的更为精确的过剩近似值,即
的更为精确的过剩近似值,即 .若每次都取最简分数,那么第三次用“调日法”后可得
.若每次都取最简分数,那么第三次用“调日法”后可得 的近似分数为( )
的近似分数为( )
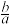 和
和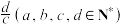 ,则
,则 是x的更为精确的不足近似值或过剩近似值我们知道
是x的更为精确的不足近似值或过剩近似值我们知道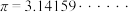 ,若令
,若令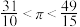 ,则第一次用“调日法”后得
,则第一次用“调日法”后得 是
是 的更为精确的过剩近似值,即
的更为精确的过剩近似值,即 .若每次都取最简分数,那么第三次用“调日法”后可得
.若每次都取最简分数,那么第三次用“调日法”后可得 的近似分数为( )
的近似分数为( )A.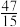 | B.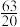 | C.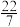 | D.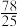 |
您最近一年使用:0次
2020-04-27更新
|
223次组卷
|
2卷引用:2019届安徽省合肥市第一中学高三下学期冲刺高考最后一次模拟数学(理)试题
名校
5 . 《九章算术》中“勾股容方”问题:“今有勾五步,股十二步,问勾中容方几何?”魏晋时期数学家刘徽在其《九章算术注》中利用出入相补原理给出了这个问题的一般解法:如图1,用对角线将长和宽分别为 和
和 的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为
的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为 ,宽为内接正方形的边长
,宽为内接正方形的边长 .由刘徽构造的图形还可以得到许多重要的结论,如图3.设
.由刘徽构造的图形还可以得到许多重要的结论,如图3.设 为斜边
为斜边 的中点,作直角三角形
的中点,作直角三角形 的内接正方形对角线
的内接正方形对角线 ,过点
,过点 作
作 于点
于点 ,则下列推理正确的是( )
,则下列推理正确的是( )

①由图1和图2面积相等得 ;
;
②由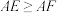 可得
可得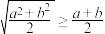 ;
;
③由 可得
可得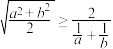 ;
;
④由 可得
可得 .
.
 和
和 的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为
的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为 ,宽为内接正方形的边长
,宽为内接正方形的边长 .由刘徽构造的图形还可以得到许多重要的结论,如图3.设
.由刘徽构造的图形还可以得到许多重要的结论,如图3.设 为斜边
为斜边 的中点,作直角三角形
的中点,作直角三角形 的内接正方形对角线
的内接正方形对角线 ,过点
,过点 作
作 于点
于点 ,则下列推理正确的是( )
,则下列推理正确的是( )
①由图1和图2面积相等得
 ;
;②由
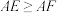 可得
可得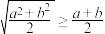 ;
;③由
 可得
可得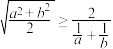 ;
;④由
 可得
可得 .
.| A.①②③④ | B.①②④ | C.②③④ | D.①③ |
您最近一年使用:0次
2020-04-27更新
|
412次组卷
|
8卷引用:2020届安徽省合肥市高三下学期4月第二次教学质量检测数学(理)试题
2020届安徽省合肥市高三下学期4月第二次教学质量检测数学(理)试题2020届安徽省合肥市高三下学期4月第二次教学质量检测文科数学试题2020届宁夏中卫市高三下学期第二次模拟考试数学(理)试题安徽省蚌埠市田家炳中学2019-2020学年高二下学期开学考试数学(文)试题(已下线)专题03 新定义问题、推理与证明-2020年高考数学(文)母题题源解密(全国Ⅱ专版)(已下线)专题12 新定义问题、推理与证明-2020年高考数学(理)母题题源解密(全国Ⅱ专版)宁夏平罗中学2023届高三上学期第一次月考数学(理)试题福建泉州实验中学2020-2021学年高一年10月月考数学试题
6 . 在数学中,泰勒级数用无限项连加式——级数来表示一个函数,包括正弦,余弦,正切三角函数等等,其中泰勒级数是以于1715年发表了泰勒公式的英国数学家布鲁克•泰勒(Sir Brook Taylor)的名字来命名的.1715年,泰勒提出了一个常用的方法来构建这一系列级数并适用于所有函数,这就是后来被人们所熟知的泰勒级数,并建立了如下指数函数公式: ,其中
,其中 ,
, ,
,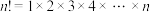 ,例如:
,例如: ,
, ,
,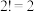 ,
, .试用上述公式估计
.试用上述公式估计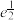 的近似值为(精确到0.001)( )
的近似值为(精确到0.001)( )
 ,其中
,其中 ,
, ,
,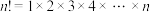 ,例如:
,例如: ,
, ,
,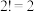 ,
, .试用上述公式估计
.试用上述公式估计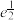 的近似值为(精确到0.001)( )
的近似值为(精确到0.001)( )| A.1.601 | B.1.642 | C.1.648 | D.1.647 |
您最近一年使用:0次
2020-03-28更新
|
817次组卷
|
7卷引用:2020届安徽省皖江名校联盟高三下学期第五次联考数学(理)试题
2020届安徽省皖江名校联盟高三下学期第五次联考数学(理)试题2020届安徽省皖江名校联盟高三下学期第五次联考数学(文)试题(已下线)第四篇数学文化03-2020年高考数学选填题专项测试(文理通用)2021届高三高考必杀技之信息阅读题--类型9 公式的理解与应用(已下线)专题13 泰勒(已下线)专题04 与函数概念与性质有关的情景化试题 - 2021-2022学年高一数学新教材情境化新题(人教A版2019必修第一册) 浙江省绍兴市诸暨市2021-2022学年高二下学期学考模拟(1)数学试题
7 . 杨辉三角是二项式系数在三角形中的一种几何排列,在中国南宋数学家杨辉1261年所著的《详解九章算法》一书中就有出现.在欧洲,帕斯卡(1623~1662)在1654年发现这一规律,比杨辉要迟了393年.如图所示,在“杨辉三角”中,从1开始箭头所指的数组成一个锯齿形数列:1,2,3,3,6,4,10,5,…,则在该数列中,第37项是
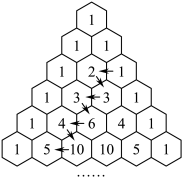
| A.153 | B.171 | C.190 | D.210 |
您最近一年使用:0次
2020-03-26更新
|
1452次组卷
|
10卷引用:2020届安徽省淮南市寿县第一中学高三下学期第七次月考数学(理)试题
2020届安徽省淮南市寿县第一中学高三下学期第七次月考数学(理)试题金科大联考2019-2020学年高三10月质量检测数学文科试题2020届陕西省安康中学高三第三次模拟考试理科数学试题云南省曲靖市第二中学、大理新世纪中学2021届高三第一次模拟考试数学(理)试题(已下线)考点17 数列的综合运用-备战2022年高考数学(理)一轮复习考点微专题河南省商丘市第一高级中学2020-2021学年高二下学期3月月考数学理科试题(已下线)专题01 数列【知识梳理】-2020-2021学年高二数学下学期期末专项复习(新人教B版2019)广东省深圳市重点中学2021-2022学年高二上学期期末数学试题福建省漳州市漳州康桥高级中学2023-2024学年高二上学期10月月考数学试题河南省郑州市第一中学2022-2023学年高二下学期期中考试数学试题
8 . 杨辉,字谦光,南宋时期杭州人.在他1261年所著的《详解九章算法》一书中,辑录了如图所示的三角形数表,称之为“开方作法本源”图,并说明此表引自11世纪中叶(约公元1050年)贾宪的《释锁算术》,并绘画了“古法七乘方图”.故此,杨辉三角又被称为“贾宪三角”.杨辉三角是一个由数字排列成的三角形数表,一般形式如下:

基于上述规律,可以推测,当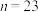 时,从左往右第22个数为
时,从左往右第22个数为_____________ .

基于上述规律,可以推测,当
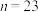 时,从左往右第22个数为
时,从左往右第22个数为
您最近一年使用:0次
2020-03-20更新
|
257次组卷
|
4卷引用:2020届安徽省六安市第一中学高三下学期模拟卷(六)数学(理)试题
2020届安徽省六安市第一中学高三下学期模拟卷(六)数学(理)试题2020届安徽省六安市第一中学高三下学期模拟卷(六)数学(文)试题(已下线)强化卷05(3月)-冲刺2020高考数学之必拿分题目强化卷(山东专版)黑龙江省哈尔滨市师大附中2019-2020学年高二下学期期中考试数学(文)试题
名校
9 . 南宋数学家杨辉研究了垛积与各类多面体体积的联系,由多面体体积公式导出相应的垛积术公式.例如方亭(正四棱台)体积为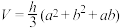 ,其中
,其中 为上底边长,
为上底边长, 为下底边长,
为下底边长, 为高.杨辉利用沈括隙积术的基础上想到:若由大小相等的圆球垛成类似于正四棱台的方垛,上底由
为高.杨辉利用沈括隙积术的基础上想到:若由大小相等的圆球垛成类似于正四棱台的方垛,上底由 个球组成,以下各层的长、宽依次各增加一个球,共有
个球组成,以下各层的长、宽依次各增加一个球,共有 层,最下层(即下底)由
层,最下层(即下底)由 个球组成,杨辉给出求方垛中物体总数的公式如下:
个球组成,杨辉给出求方垛中物体总数的公式如下: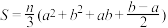 根据以上材料,我们可得
根据以上材料,我们可得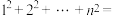
__________ .
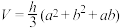 ,其中
,其中 为上底边长,
为上底边长, 为下底边长,
为下底边长, 为高.杨辉利用沈括隙积术的基础上想到:若由大小相等的圆球垛成类似于正四棱台的方垛,上底由
为高.杨辉利用沈括隙积术的基础上想到:若由大小相等的圆球垛成类似于正四棱台的方垛,上底由 个球组成,以下各层的长、宽依次各增加一个球,共有
个球组成,以下各层的长、宽依次各增加一个球,共有 层,最下层(即下底)由
层,最下层(即下底)由 个球组成,杨辉给出求方垛中物体总数的公式如下:
个球组成,杨辉给出求方垛中物体总数的公式如下: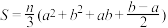 根据以上材料,我们可得
根据以上材料,我们可得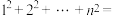
您最近一年使用:0次
2020-03-09更新
|
151次组卷
|
2卷引用:2020届安徽省六安市第一中学高三下学期模拟卷(五)数学(文)试题
名校
10 . 在《九章算术》方田章圆田术(刘徽注)中指出,“割之弥细,所失弥少,制之又割,以至于不可割,则与圆周合体而无所失矣.”注述中所用的割圆术是一种无限与有限的转化过程,比如在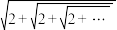 中“…”即代表无限次重复,但原式却是个定值x,这可以通过方程
中“…”即代表无限次重复,但原式却是个定值x,这可以通过方程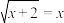 确定出来
确定出来 ,类比上述结论可得
,类比上述结论可得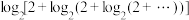 的正值为
的正值为
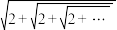 中“…”即代表无限次重复,但原式却是个定值x,这可以通过方程
中“…”即代表无限次重复,但原式却是个定值x,这可以通过方程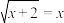 确定出来
确定出来 ,类比上述结论可得
,类比上述结论可得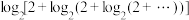 的正值为
的正值为| A.1 | B. | C.2 | D.4 |
您最近一年使用:0次
2019-10-21更新
|
900次组卷
|
5卷引用:安徽省全国示范高中名校2019-2020学年高三上学期9月月考数学(理)试题



