12-13高一上·北京·期末
名校
1 . 已知集合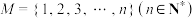 ,若集合
,若集合 ,且对任意的
,且对任意的 ,存在
,存在 ,
,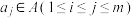 ,使得
,使得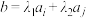 (其中
(其中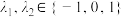 ),则称集合
),则称集合 为集合
为集合 的一个
的一个 元基底.
元基底.
(1)分别判断下列集合 是否为集合
是否为集合 的一个二元基底,并说明理由;
的一个二元基底,并说明理由;
①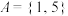 ,
,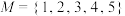 ;
;
②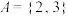 ,
, .
.
(2)若集合 是集合
是集合 的一个
的一个 元基底,证明:
元基底,证明: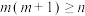 ;
;
(3)若集合 为集合
为集合 的一个
的一个 元基底,求出
元基底,求出 的最小可能值,并写出当
的最小可能值,并写出当 取最小值时
取最小值时 的一个基底
的一个基底 .
.
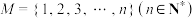 ,若集合
,若集合 ,且对任意的
,且对任意的 ,存在
,存在 ,
,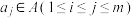 ,使得
,使得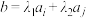 (其中
(其中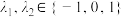 ),则称集合
),则称集合 为集合
为集合 的一个
的一个 元基底.
元基底.(1)分别判断下列集合
 是否为集合
是否为集合 的一个二元基底,并说明理由;
的一个二元基底,并说明理由;①
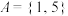 ,
,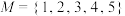 ;
;②
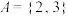 ,
, .
.(2)若集合
 是集合
是集合 的一个
的一个 元基底,证明:
元基底,证明: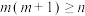 ;
;(3)若集合
 为集合
为集合 的一个
的一个 元基底,求出
元基底,求出 的最小可能值,并写出当
的最小可能值,并写出当 取最小值时
取最小值时 的一个基底
的一个基底 .
.
您最近一年使用:0次
2023-03-22更新
|
1067次组卷
|
15卷引用:北京市第四中学2023届高三阶段性考试(零模)数学试题
(已下线)北京市第四中学2023届高三阶段性考试(零模)数学试题北京市汇文中学教育集团2022-2023学年高二下学期期中考试数学试题北京市广渠门中学2022-2023学年高二下学期期中考试数学试题北京市第五十七中学2022-2023学年高二下学期期中测试数学试题北京市第二中学2022-2023学年高二下学期第六学段(期末)考试数学试题(已下线)上海高二下学期期末真题精选(压轴60题35个考点专练)-【满分全攻略】2022-2023学年高二数学下学期核心考点+重难点讲练与测试(沪教版2020选修一+选修二)(已下线)难关必刷01集合的综合问题(3种题型40题专项训练)-【满分全攻略】(人教A版2019必修第一册)(已下线)2011-2012学年北京市育园中学高一第一学期期末考试数学北京市第二中学2020-2021学年高一下学期期末数学试题北京市清华大学附属中学2022届高三下学期数学统练6试题北京市丰台区丰台第二中学2023届高三上学期12月月考数学试题上海市进才中学2020-2021学年高二下学期期末数学试题(已下线)计数原理与排列组合【北京专用】专题05计数原理(第二部分)-高二上学期名校期末好题汇编(已下线)专题01 数列(6大考点经典基础练+优选提升练)-【好题汇编】备战2023-2024学年高二数学下学期期末真题分类汇编(新高考专用)
2 . 已知集合 ,对于集合
,对于集合 的非空子集
的非空子集 .若
.若 中存在三个互不相同的元素
中存在三个互不相同的元素 ,
, ,
, ,使得
,使得 ,
, ,
, 均属于
均属于 ,则称集合
,则称集合 是集合
是集合 的“期待子集”.
的“期待子集”.
(1)试判断集合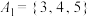 ,
,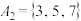 是否为集合
是否为集合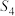 的“期待子集”;(直接写出答案,不必说明理由)
的“期待子集”;(直接写出答案,不必说明理由)
(2)如果一个集合中含有三个元素 ,
, ,
, ,同时满足①
,同时满足①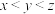 ,②
,②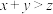 ,③
,③ 为偶数.那么称该集合具有性质
为偶数.那么称该集合具有性质 .对于集合
.对于集合 的非空子集
的非空子集 ,证明:集合
,证明:集合 是集合
是集合 的“期待子集”的充要条件是集合
的“期待子集”的充要条件是集合 具有性质
具有性质 ;
;
(3)若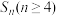 的任意含有
的任意含有 个元素的子集都是集合
个元素的子集都是集合 的“期待子集”,求
的“期待子集”,求 的最小值.
的最小值.
 ,对于集合
,对于集合 的非空子集
的非空子集 .若
.若 中存在三个互不相同的元素
中存在三个互不相同的元素 ,
, ,
, ,使得
,使得 ,
, ,
, 均属于
均属于 ,则称集合
,则称集合 是集合
是集合 的“期待子集”.
的“期待子集”.(1)试判断集合
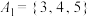 ,
,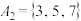 是否为集合
是否为集合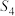 的“期待子集”;(直接写出答案,不必说明理由)
的“期待子集”;(直接写出答案,不必说明理由)(2)如果一个集合中含有三个元素
 ,
, ,
, ,同时满足①
,同时满足①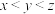 ,②
,②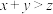 ,③
,③ 为偶数.那么称该集合具有性质
为偶数.那么称该集合具有性质 .对于集合
.对于集合 的非空子集
的非空子集 ,证明:集合
,证明:集合 是集合
是集合 的“期待子集”的充要条件是集合
的“期待子集”的充要条件是集合 具有性质
具有性质 ;
;(3)若
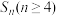 的任意含有
的任意含有 个元素的子集都是集合
个元素的子集都是集合 的“期待子集”,求
的“期待子集”,求 的最小值.
的最小值.
您最近一年使用:0次
2023-03-21更新
|
1048次组卷
|
6卷引用:北京市丰台区2023届高三一模数学试题
北京市丰台区2023届高三一模数学试题专题12压轴题汇总(10、15、21题)专题01集合与常用逻辑(已下线)北京市丰台区2023届高三下学期3月一模数学试题变式题16-21北京卷专题02集合(解答题)(已下线)第一章 集合与逻辑(压轴题专练)-速记·巧练(沪教版2020必修第一册)
3 . 已知数集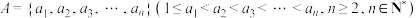 .如果对任意的
.如果对任意的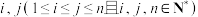 ,
,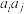 与
与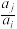 两数中至少有一个属于A,则称数集A具有性质P.
两数中至少有一个属于A,则称数集A具有性质P.
(1)分别判断数集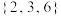 ,
,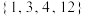 是否具有性质
是否具有性质 ,并说明理由;
,并说明理由;
(2)设数集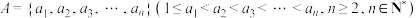 具有性质P.若
具有性质P.若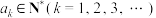 ,证明:对任意
,证明:对任意 都有
都有 是
是 的因数.
的因数.
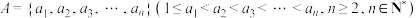 .如果对任意的
.如果对任意的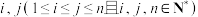 ,
,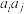 与
与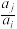 两数中至少有一个属于A,则称数集A具有性质P.
两数中至少有一个属于A,则称数集A具有性质P.(1)分别判断数集
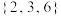 ,
,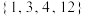 是否具有性质
是否具有性质 ,并说明理由;
,并说明理由;(2)设数集
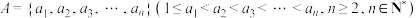 具有性质P.若
具有性质P.若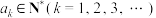 ,证明:对任意
,证明:对任意 都有
都有 是
是 的因数.
的因数.
您最近一年使用:0次
名校
4 . 若集合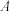 具有以下性质:(i)
具有以下性质:(i)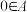 且
且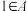 ;(ⅱ)若
;(ⅱ)若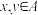 ,则
,则 ,且当
,且当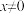 时,
时,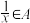 ,则称集合
,则称集合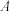 为“闭集”.
为“闭集”.
(1)试判断集合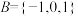 是否为“闭集”,并说明理由;
是否为“闭集”,并说明理由;
(2)设集合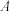 是“闭集”,求证:若
是“闭集”,求证:若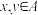 ,则
,则 ;
;
(3)若集合 是一个“闭集”,判断命题“若
是一个“闭集”,判断命题“若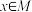 ,则
,则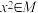 ”的真假,并说明理由.
”的真假,并说明理由.
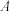 具有以下性质:(i)
具有以下性质:(i)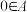 且
且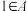 ;(ⅱ)若
;(ⅱ)若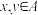 ,则
,则 ,且当
,且当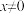 时,
时,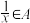 ,则称集合
,则称集合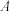 为“闭集”.
为“闭集”.(1)试判断集合
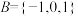 是否为“闭集”,并说明理由;
是否为“闭集”,并说明理由;(2)设集合
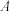 是“闭集”,求证:若
是“闭集”,求证:若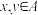 ,则
,则 ;
;(3)若集合
 是一个“闭集”,判断命题“若
是一个“闭集”,判断命题“若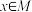 ,则
,则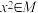 ”的真假,并说明理由.
”的真假,并说明理由.
您最近一年使用:0次
2022-10-19更新
|
947次组卷
|
3卷引用:第一章 集合与常用逻辑用语 (单元测)
名校
5 . 已知集合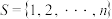 (
( 且
且 ),
), ,且
,且 .若对任意
.若对任意 ,
, ,当
,当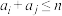 时,存在
时,存在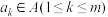 ,使得
,使得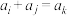 ,则称
,则称 是
是 的
的 元完美子集.
元完美子集.
(1)判断下列集合是否是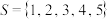 的3元完美子集,并说明理由;
的3元完美子集,并说明理由;
①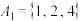 ;
;
②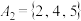 ;
;
(2)若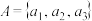 是
是 的3元完美子集,求
的3元完美子集,求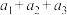 的最小值;
的最小值;
(3)若 是
是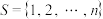 (
( 且
且 )的
)的 元完美子集,求证:
元完美子集,求证: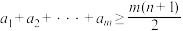 .
.
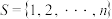 (
( 且
且 ),
), ,且
,且 .若对任意
.若对任意 ,
, ,当
,当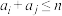 时,存在
时,存在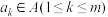 ,使得
,使得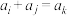 ,则称
,则称 是
是 的
的 元完美子集.
元完美子集.(1)判断下列集合是否是
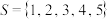 的3元完美子集,并说明理由;
的3元完美子集,并说明理由;①
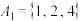 ;
; ②
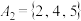 ;
;(2)若
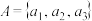 是
是 的3元完美子集,求
的3元完美子集,求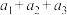 的最小值;
的最小值;(3)若
 是
是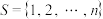 (
( 且
且 )的
)的 元完美子集,求证:
元完美子集,求证: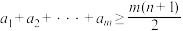 .
.
您最近一年使用:0次
2022-05-12更新
|
738次组卷
|
4卷引用:专题16 数列新定义题的解法 微点2 数列新定义题综合训练
(已下线)专题16 数列新定义题的解法 微点2 数列新定义题综合训练北京市第二中学2022—2023学年高一下学期第六学段阶段性考试数学试题北京师范大学附属中学2021-2022学年高一下学期期中考试数学试题重庆市杨家坪中学2022-2023学年高一上学期10月月考数学试题
名校
解题方法
6 . 设 为非空集合,定义
为非空集合,定义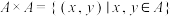 (其中
(其中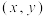 表示有序对),称
表示有序对),称 的任意非空子集
的任意非空子集 为
为 上的一个关系.例如
上的一个关系.例如 时,
时, 与
与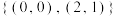 都是
都是 上的关系.设
上的关系.设 为非空集合
为非空集合 上的关系.给出如下定义:①(自反性)若对任意
上的关系.给出如下定义:①(自反性)若对任意 ,有
,有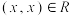 ,则称
,则称 在
在 上是自反的;②(对称性)若对任意
上是自反的;②(对称性)若对任意 ,有
,有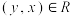 ,则称
,则称 在
在 上是对称的;③(传递性)若对任意
上是对称的;③(传递性)若对任意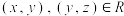 ,有
,有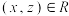 ,则称
,则称 在
在 上是传递的.如果
上是传递的.如果 上关系
上关系 同时满足上述3条性质,则称
同时满足上述3条性质,则称 为
为 上的等价关系.任给集合
上的等价关系.任给集合 ,定义
,定义 为
为 .
.
(1)若 ,问:
,问: 上关系有多少个?
上关系有多少个? 上等价关系有多少个?(不必说明理由)
上等价关系有多少个?(不必说明理由)
(2)若集合 有
有 个元素
个元素 ,
, 的非空子集
的非空子集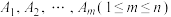 两两交集为空集,且
两两交集为空集,且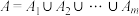 ,求证:
,求证: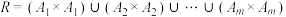 为
为 上的等价关系.
上的等价关系.
(3)若集合 有
有 个元素
个元素 ,问:对
,问:对 上的任意等价关系
上的任意等价关系 ,是否存在
,是否存在 的非空子集
的非空子集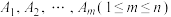 ,其中任意两个交集为空集,且
,其中任意两个交集为空集,且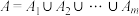 ,使得
,使得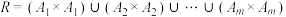 ?请判断并说明理由.
?请判断并说明理由.
 为非空集合,定义
为非空集合,定义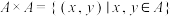 (其中
(其中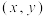 表示有序对),称
表示有序对),称 的任意非空子集
的任意非空子集 为
为 上的一个关系.例如
上的一个关系.例如 时,
时, 与
与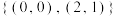 都是
都是 上的关系.设
上的关系.设 为非空集合
为非空集合 上的关系.给出如下定义:①(自反性)若对任意
上的关系.给出如下定义:①(自反性)若对任意 ,有
,有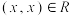 ,则称
,则称 在
在 上是自反的;②(对称性)若对任意
上是自反的;②(对称性)若对任意 ,有
,有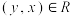 ,则称
,则称 在
在 上是对称的;③(传递性)若对任意
上是对称的;③(传递性)若对任意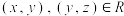 ,有
,有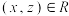 ,则称
,则称 在
在 上是传递的.如果
上是传递的.如果 上关系
上关系 同时满足上述3条性质,则称
同时满足上述3条性质,则称 为
为 上的等价关系.任给集合
上的等价关系.任给集合 ,定义
,定义 为
为 .
.(1)若
 ,问:
,问: 上关系有多少个?
上关系有多少个? 上等价关系有多少个?(不必说明理由)
上等价关系有多少个?(不必说明理由)(2)若集合
 有
有 个元素
个元素 ,
, 的非空子集
的非空子集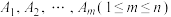 两两交集为空集,且
两两交集为空集,且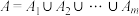 ,求证:
,求证: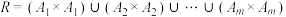 为
为 上的等价关系.
上的等价关系.(3)若集合
 有
有 个元素
个元素 ,问:对
,问:对 上的任意等价关系
上的任意等价关系 ,是否存在
,是否存在 的非空子集
的非空子集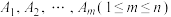 ,其中任意两个交集为空集,且
,其中任意两个交集为空集,且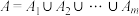 ,使得
,使得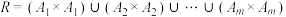 ?请判断并说明理由.
?请判断并说明理由.
您最近一年使用:0次
名校
7 . 设集合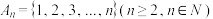 ,集合
,集合 ,如果对于任意元素
,如果对于任意元素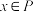 ,都有
,都有 或
或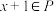 ,则称集合
,则称集合 为
为 的自邻集.记
的自邻集.记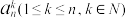 为集合
为集合 的所有自邻集中最大元素为
的所有自邻集中最大元素为 的集合的个数.
的集合的个数.
(1)直接判断集合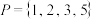 和
和 是否为
是否为 的自邻集;
的自邻集;
(2)比较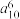 和
和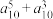 的大小,并说明理由;
的大小,并说明理由;
(3)求证: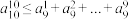 .
.
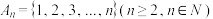 ,集合
,集合 ,如果对于任意元素
,如果对于任意元素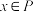 ,都有
,都有 或
或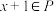 ,则称集合
,则称集合 为
为 的自邻集.记
的自邻集.记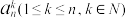 为集合
为集合 的所有自邻集中最大元素为
的所有自邻集中最大元素为 的集合的个数.
的集合的个数.(1)直接判断集合
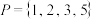 和
和 是否为
是否为 的自邻集;
的自邻集;(2)比较
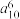 和
和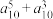 的大小,并说明理由;
的大小,并说明理由;(3)求证:
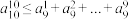 .
.
您最近一年使用:0次
名校
8 . 求已知集合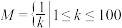 ,且
,且 ,
, ,其中
,其中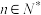 ,且
,且 .若
.若 ,且对集合
,且对集合 中的任意两个元素
中的任意两个元素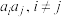 都有
都有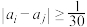 则称集合
则称集合 有性质
有性质 .
.
(1)判断集合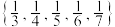 是否具有性质
是否具有性质 ;
;
(2)若集合 具有性质
具有性质 .
.
①求证: 的最大值大于等于
的最大值大于等于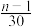 ;
;
②求 的元素个数
的元素个数 的最大值.
的最大值.
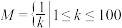 ,且
,且 ,
, ,其中
,其中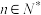 ,且
,且 .若
.若 ,且对集合
,且对集合 中的任意两个元素
中的任意两个元素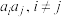 都有
都有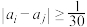 则称集合
则称集合 有性质
有性质 .
.(1)判断集合
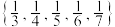 是否具有性质
是否具有性质 ;
;(2)若集合
 具有性质
具有性质 .
.①求证:
 的最大值大于等于
的最大值大于等于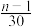 ;
;②求
 的元素个数
的元素个数 的最大值.
的最大值.
您最近一年使用:0次
名校
9 . 已知集合 ,x、
,x、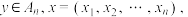
 ,其中
,其中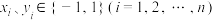 .定义
.定义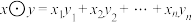 ,若
,若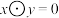 ,则称x与y正交.
,则称x与y正交.
(1)若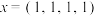 ,写出
,写出 中与x正交的所有元素;
中与x正交的所有元素;
(2)令 ,若
,若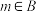 ,证明:
,证明: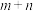 为偶数;
为偶数;
(3)若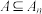 ,且A中任意两个元素均正交,分别求出
,且A中任意两个元素均正交,分别求出 ,14时,A中最多可以有多少个元素.
,14时,A中最多可以有多少个元素.
 ,x、
,x、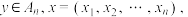
 ,其中
,其中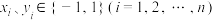 .定义
.定义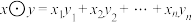 ,若
,若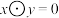 ,则称x与y正交.
,则称x与y正交.(1)若
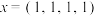 ,写出
,写出 中与x正交的所有元素;
中与x正交的所有元素;(2)令
 ,若
,若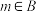 ,证明:
,证明: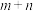 为偶数;
为偶数;(3)若
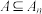 ,且A中任意两个元素均正交,分别求出
,且A中任意两个元素均正交,分别求出 ,14时,A中最多可以有多少个元素.
,14时,A中最多可以有多少个元素.
您最近一年使用:0次
2023-02-03更新
|
661次组卷
|
5卷引用:上海市实验学校2022-2023学年高一上学期期末数学试题
上海市实验学校2022-2023学年高一上学期期末数学试题(已下线)难关必刷01集合的综合问题(3种题型30题专项训练)-【满分全攻略】(沪教版2020必修第一册)北京市广渠门中学2023-2024学年高二上学期10月月考数学试题(已下线)高一上学期期末复习【第一章 集合与常用逻辑用语】拔尖-举一反三系列(已下线)高一上学期期末考试解答题压轴题50题专练-举一反三系列
10 . 若正整数集合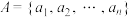 (
(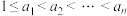 ,n为正整数,且
,n为正整数,且 )满足:对任意的
)满足:对任意的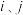 (
( ,
,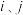 均为正整数),两数
均为正整数),两数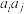 与
与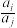 中至少有一个属于
中至少有一个属于 ,则称
,则称 具有性质
具有性质 .(其中
.(其中 ,
, ,…,
,…, 表示
表示 个变量)
个变量)
(1)分别判断集合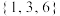 与
与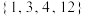 是否具有性质
是否具有性质 ;
;
(2)设正整数集合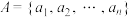 (
(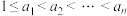 ,
, 为正整数,且
为正整数,且 )具有性质
)具有性质 ,证明:对任意
,证明:对任意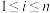 (i为正整数),
(i为正整数), 都是
都是 的因数;
的因数;
(3)若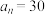 ,求
,求 的最大值.
的最大值.
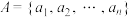 (
(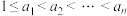 ,n为正整数,且
,n为正整数,且 )满足:对任意的
)满足:对任意的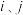 (
( ,
,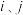 均为正整数),两数
均为正整数),两数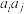 与
与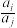 中至少有一个属于
中至少有一个属于 ,则称
,则称 具有性质
具有性质 .(其中
.(其中 ,
, ,…,
,…, 表示
表示 个变量)
个变量)(1)分别判断集合
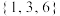 与
与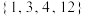 是否具有性质
是否具有性质 ;
;(2)设正整数集合
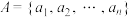 (
(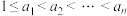 ,
, 为正整数,且
为正整数,且 )具有性质
)具有性质 ,证明:对任意
,证明:对任意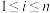 (i为正整数),
(i为正整数), 都是
都是 的因数;
的因数;(3)若
 ,求
,求 的最大值.
的最大值.
您最近一年使用:0次



