1 . 设数列 的前
的前 项和为
项和为 .若对任意的正整数
.若对任意的正整数 ,总存在正整数
,总存在正整数 ,使得
,使得 ,则称
,则称 是“
是“ 数列”.
数列”.
(1)若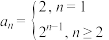 ,判断数列
,判断数列 是否是“
是否是“ 数列”;
数列”;
(2)设 是等差数列,其首项
是等差数列,其首项 ,公差
,公差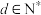 ,且
,且 是“
是“ 数列”,
数列”,
①求 的值;
的值;
②设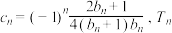 为数列
为数列 的前
的前 项和,证明:
项和,证明:
 的前
的前 项和为
项和为 .若对任意的正整数
.若对任意的正整数 ,总存在正整数
,总存在正整数 ,使得
,使得 ,则称
,则称 是“
是“ 数列”.
数列”.(1)若
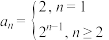 ,判断数列
,判断数列 是否是“
是否是“ 数列”;
数列”;(2)设
 是等差数列,其首项
是等差数列,其首项 ,公差
,公差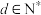 ,且
,且 是“
是“ 数列”,
数列”,①求
 的值;
的值;②设
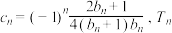 为数列
为数列 的前
的前 项和,证明:
项和,证明:
您最近一年使用:0次
2 . 若有穷数列 (
( 是正整数),满足
是正整数),满足 (
( ,且
,且 ,就称该数列为“
,就称该数列为“ 数列”.
数列”.
(1)已知数列 是项数为7的
是项数为7的 数列,且
数列,且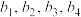 成等比数列,
成等比数列,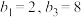 ,试写出
,试写出 的每一项;
的每一项;
(2)已知 是项数为
是项数为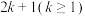 的
的 数列,且
数列,且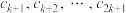 构成首项为100,公差为
构成首项为100,公差为 的等差数列,数列
的等差数列,数列 的前
的前 项和为
项和为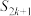 ,则当
,则当 为何值时,
为何值时,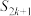 取到最大值?最大值为多少?
取到最大值?最大值为多少?
(3)对于给定的正整数 ,试写出所有项数不超过
,试写出所有项数不超过 的
的 数列,使得
数列,使得 成为数列中的连续项;当
成为数列中的连续项;当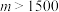 时,试求这些
时,试求这些 数列的前2024项和
数列的前2024项和 .
.
 (
( 是正整数),满足
是正整数),满足 (
( ,且
,且 ,就称该数列为“
,就称该数列为“ 数列”.
数列”.(1)已知数列
 是项数为7的
是项数为7的 数列,且
数列,且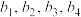 成等比数列,
成等比数列,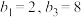 ,试写出
,试写出 的每一项;
的每一项;(2)已知
 是项数为
是项数为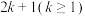 的
的 数列,且
数列,且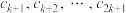 构成首项为100,公差为
构成首项为100,公差为 的等差数列,数列
的等差数列,数列 的前
的前 项和为
项和为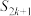 ,则当
,则当 为何值时,
为何值时,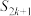 取到最大值?最大值为多少?
取到最大值?最大值为多少?(3)对于给定的正整数
 ,试写出所有项数不超过
,试写出所有项数不超过 的
的 数列,使得
数列,使得 成为数列中的连续项;当
成为数列中的连续项;当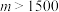 时,试求这些
时,试求这些 数列的前2024项和
数列的前2024项和 .
.
您最近一年使用:0次
2024-04-10更新
|
608次组卷
|
2卷引用:海南省琼海市嘉积中学2023-2024学年高三下学期一模考试数学试题
3 . 由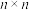 个数排列成
个数排列成 行
行 列的数表称为
列的数表称为 行
行 列的矩阵,简称
列的矩阵,简称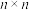 矩阵,也称为
矩阵,也称为 阶方阵,记作:
阶方阵,记作: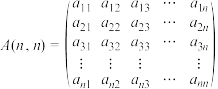 其中
其中 表示矩阵
表示矩阵 中第
中第 行第
行第 列的数.已知三个
列的数.已知三个 阶方阵分别为
阶方阵分别为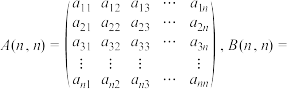
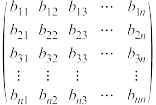 ,
,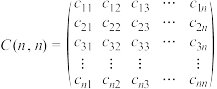 ,其中
,其中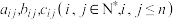 分别表示
分别表示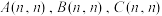 中第
中第 行第
行第 列的数.若
列的数.若 ,则称
,则称 是
是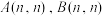 生成的线性矩阵.
生成的线性矩阵.
(1)已知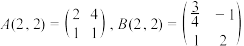 ,若
,若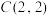 是
是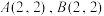 生成的线性矩阵,且
生成的线性矩阵,且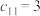 ,求
,求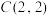 ;
;
(2)已知 ,矩阵
,矩阵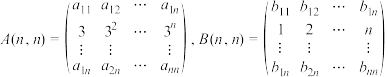 ,矩阵
,矩阵 是
是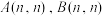 生成的线性矩阵,且
生成的线性矩阵,且 .
.
(i)求 ;
;
(ii)已知数列 满足
满足 ,数列
,数列 满足
满足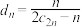 ,数列
,数列 的前
的前 项和记为
项和记为 ,是否存在正整数
,是否存在正整数 ,使
,使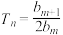 成立?若存在,求出所有的正整数对
成立?若存在,求出所有的正整数对 ;若不存在,请说明理由.
;若不存在,请说明理由.
 个数排列成
个数排列成 行
行 列的数表称为
列的数表称为 行
行 列的矩阵,简称
列的矩阵,简称 矩阵,也称为
矩阵,也称为 阶方阵,记作:
阶方阵,记作: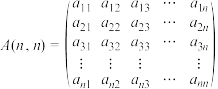 其中
其中 表示矩阵
表示矩阵 中第
中第 行第
行第 列的数.已知三个
列的数.已知三个 阶方阵分别为
阶方阵分别为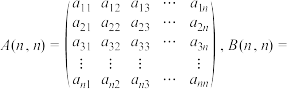
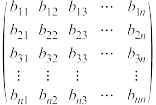 ,
,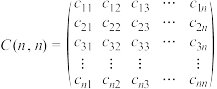 ,其中
,其中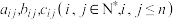 分别表示
分别表示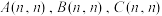 中第
中第 行第
行第 列的数.若
列的数.若 ,则称
,则称 是
是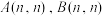 生成的线性矩阵.
生成的线性矩阵.(1)已知
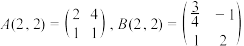 ,若
,若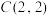 是
是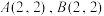 生成的线性矩阵,且
生成的线性矩阵,且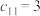 ,求
,求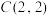 ;
;(2)已知
 ,矩阵
,矩阵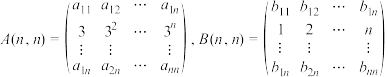 ,矩阵
,矩阵 是
是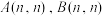 生成的线性矩阵,且
生成的线性矩阵,且 .
.(i)求
 ;
;(ii)已知数列
 满足
满足 ,数列
,数列 满足
满足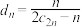 ,数列
,数列 的前
的前 项和记为
项和记为 ,是否存在正整数
,是否存在正整数 ,使
,使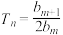 成立?若存在,求出所有的正整数对
成立?若存在,求出所有的正整数对 ;若不存在,请说明理由.
;若不存在,请说明理由.
您最近一年使用:0次



