22-23高一下·上海宝山·期中
名校
解题方法
1 . 已知函数 与
与 的定义域为R,若对任意区间
的定义域为R,若对任意区间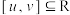 ,存在
,存在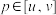 且
且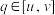 ,使
,使 ,则
,则 是
是 的生成函数.
的生成函数.
(1)求证: 是
是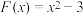 的生成函数;
的生成函数;
(2)若 是
是 的生成函数,判断并证明
的生成函数,判断并证明 的单调性;
的单调性;
(3)若 是
是 的生成函数,实数
的生成函数,实数 ,求
,求 的一个生成函数.
的一个生成函数.
 与
与 的定义域为R,若对任意区间
的定义域为R,若对任意区间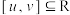 ,存在
,存在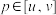 且
且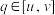 ,使
,使 ,则
,则 是
是 的生成函数.
的生成函数.(1)求证:
 是
是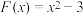 的生成函数;
的生成函数;(2)若
 是
是 的生成函数,判断并证明
的生成函数,判断并证明 的单调性;
的单调性;(3)若
 是
是 的生成函数,实数
的生成函数,实数 ,求
,求 的一个生成函数.
的一个生成函数.
您最近一年使用:0次
2023-05-05更新
|
559次组卷
|
4卷引用:第3课时 课后 函数的单调性(完成)
(已下线)第3课时 课后 函数的单调性(完成)上海交通大学附属中学2022-2023学年高一下学期期中数学试题湖南省长沙市明德中学2022-2023学年高一下学期5月月考数学试题(已下线)5.2.2 函数的单调性-数学同步精品课堂(沪教版2020必修第一册)
20-21高一下·上海宝山·期末
名校
2 . 若定义域为 的函数
的函数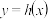 满足:对于任意
满足:对于任意 ,都有
,都有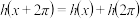 ,则称函数
,则称函数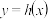 具有性质
具有性质 .
.
(1)设函数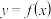 ,
,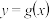 的表达式分别为
的表达式分别为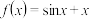 ,
, ,判断函数
,判断函数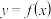 与
与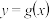 是否具有性质
是否具有性质 ,说明理由;
,说明理由;
(2)设函数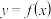 的表达式为
的表达式为 ,是否存在
,是否存在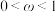 以及
以及 ,使得函数
,使得函数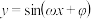 具有性质
具有性质 ?若存在,求出
?若存在,求出 ,
, 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)设函数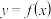 具有性质
具有性质 ,且在
,且在 上的值域恰为
上的值域恰为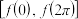 ;以
;以 为周期的函数
为周期的函数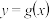 的表达式为
的表达式为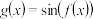 ,且在开区间
,且在开区间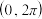 上有且仅有一个零点,求证:
上有且仅有一个零点,求证: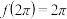 .
.
 的函数
的函数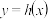 满足:对于任意
满足:对于任意 ,都有
,都有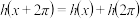 ,则称函数
,则称函数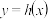 具有性质
具有性质 .
.(1)设函数
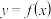 ,
,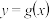 的表达式分别为
的表达式分别为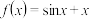 ,
, ,判断函数
,判断函数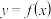 与
与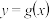 是否具有性质
是否具有性质 ,说明理由;
,说明理由;(2)设函数
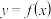 的表达式为
的表达式为 ,是否存在
,是否存在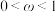 以及
以及 ,使得函数
,使得函数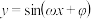 具有性质
具有性质 ?若存在,求出
?若存在,求出 ,
, 的值;若不存在,说明理由;
的值;若不存在,说明理由;(3)设函数
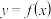 具有性质
具有性质 ,且在
,且在 上的值域恰为
上的值域恰为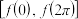 ;以
;以 为周期的函数
为周期的函数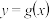 的表达式为
的表达式为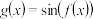 ,且在开区间
,且在开区间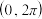 上有且仅有一个零点,求证:
上有且仅有一个零点,求证: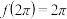 .
.
您最近一年使用:0次
2021-07-12更新
|
1754次组卷
|
9卷引用:7.3 三角函数的图像和性质(难点)(课堂培优)-2021-2022学年高一数学课后培优练(苏教版2019必修第一册)
(已下线)7.3 三角函数的图像和性质(难点)(课堂培优)-2021-2022学年高一数学课后培优练(苏教版2019必修第一册)上海交通大学附属中学2020-2021学年高一下学期期末数学试题(已下线)5.4三角函数的图象与性质(课堂探究+专题训练)-2021-2022学年高一数学课堂精选(人教A版2019必修第一册)(已下线)5.4 三角函数的图象与性质-2021-2022学年高一数学同步辅导讲义与检测(人教A版2019必修第一册)(已下线)第7章 三角函数 单元测试(单元综合检测)(难点)(单元培优)-2021-2022学年高一数学课后培优练(苏教版2019必修第一册)(已下线)期末重难点突破专题01-【尖子生专用】2021-2022学年高一数学考点培优训练(人教A版2019必修第一册)(已下线)第五章 三角函数单元检测卷(能力挑战)【一堂好课】2021-2022学年高一数学上学期同步精品课堂(人教A版2019必修第一册)上海师范大学附属中学2023届高三上学期10月月考数学试题上海市复兴高级中学2021-2022学年高一下学期期中数学试题
20-21高一上·上海金山·期末
名校
解题方法
3 . 若两个函数 和
和 对任意
对任意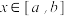 都有
都有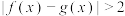 ,则称函数
,则称函数 和
和 在上
在上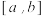 是疏远的.
是疏远的.
(1)已知命题“函数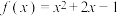 和
和 在
在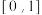 上是疏远的”,试判断该命题的真假.若该命题为真命题,请予以证明;若为假命题,请举反例;
上是疏远的”,试判断该命题的真假.若该命题为真命题,请予以证明;若为假命题,请举反例;
(2)若函数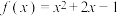 和
和 在
在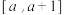 上是疏远的,求实数
上是疏远的,求实数 的取值范围;
的取值范围;
(3)已知常数 ,若函数
,若函数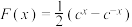 与
与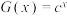 在
在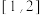 上是疏远的,求实数
上是疏远的,求实数 的取值范围.
的取值范围.
 和
和 对任意
对任意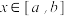 都有
都有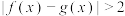 ,则称函数
,则称函数 和
和 在上
在上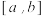 是疏远的.
是疏远的.(1)已知命题“函数
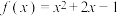 和
和 在
在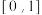 上是疏远的”,试判断该命题的真假.若该命题为真命题,请予以证明;若为假命题,请举反例;
上是疏远的”,试判断该命题的真假.若该命题为真命题,请予以证明;若为假命题,请举反例;(2)若函数
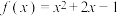 和
和 在
在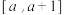 上是疏远的,求实数
上是疏远的,求实数 的取值范围;
的取值范围;(3)已知常数
 ,若函数
,若函数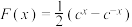 与
与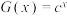 在
在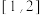 上是疏远的,求实数
上是疏远的,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2021-09-15更新
|
860次组卷
|
4卷引用:4.2指数函数C卷



