1 . 在三棱锥 中,三条棱
中,三条棱 两两垂直,且
两两垂直,且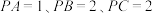 .若点
.若点 为三棱锥
为三棱锥 的外接球球面上任意一点,则
的外接球球面上任意一点,则 到面
到面 距离的最大值为
距离的最大值为______ .
 中,三条棱
中,三条棱 两两垂直,且
两两垂直,且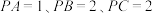 .若点
.若点 为三棱锥
为三棱锥 的外接球球面上任意一点,则
的外接球球面上任意一点,则 到面
到面 距离的最大值为
距离的最大值为
您最近一年使用:0次
2 . 已知三棱锥P-ABC的平面展开图中,四边形ABCD为边长等于 的正方形,△ABE和△BCF均为正三角形,在三棱锥P-ABC中:
的正方形,△ABE和△BCF均为正三角形,在三棱锥P-ABC中:

(1)证明:平面PAC⊥平面ABC;
(2)若点M为棱PA上一点且 ,求二面角P-BC-M的余弦值.
,求二面角P-BC-M的余弦值.
 的正方形,△ABE和△BCF均为正三角形,在三棱锥P-ABC中:
的正方形,△ABE和△BCF均为正三角形,在三棱锥P-ABC中:
(1)证明:平面PAC⊥平面ABC;
(2)若点M为棱PA上一点且
 ,求二面角P-BC-M的余弦值.
,求二面角P-BC-M的余弦值.
您最近一年使用:0次
3 . 半径分别为6、6、6、7的四个球两两外切.它们都内切于一个大球,则大球的半径是________
您最近一年使用:0次
名校
4 . 下面左边的平行四边形ABCD是由6个正三角形构成,将它沿虚线折起来,可以得到如右图所示的粽子形状的六面体,在这个六面体中,AB与CD夹角的余弦值是( ).


| A.0 | B.1 | C. | D.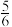 |
您最近一年使用:0次
2019-01-29更新
|
338次组卷
|
2卷引用:2018年全国高中数学联赛天津市预赛
名校
5 . 如图,在四面体 中,已知
中,已知 两两互相垂直,且
两两互相垂直,且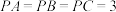 ,则在该四面体表面上与点
,则在该四面体表面上与点 距离为
距离为 的点形成的曲线段的总长度为( )
的点形成的曲线段的总长度为( )
 中,已知
中,已知 两两互相垂直,且
两两互相垂直,且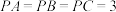 ,则在该四面体表面上与点
,则在该四面体表面上与点 距离为
距离为 的点形成的曲线段的总长度为( )
的点形成的曲线段的总长度为( )A.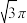 | B. |
C.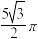 | D.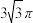 |
您最近一年使用:0次
名校
6 . 四面体ABCD中,已知 ,
,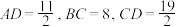 ,则异面直线AC与BD所成角的正弦值是
,则异面直线AC与BD所成角的正弦值是_____ .
 ,
,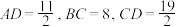 ,则异面直线AC与BD所成角的正弦值是
,则异面直线AC与BD所成角的正弦值是
您最近一年使用:0次
2019-01-28更新
|
302次组卷
|
2卷引用:2018年全国高中数学联赛辽宁省预赛
7 . 四棱锥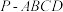 的底面
的底面 是一个顶角为
是一个顶角为 的菱形,每个侧面与底面的夹角都是
的菱形,每个侧面与底面的夹角都是 ,棱锥内有一点
,棱锥内有一点 到底面及各侧面的距离皆为1,则棱锥的体积为
到底面及各侧面的距离皆为1,则棱锥的体积为______ .
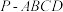 的底面
的底面 是一个顶角为
是一个顶角为 的菱形,每个侧面与底面的夹角都是
的菱形,每个侧面与底面的夹角都是 ,棱锥内有一点
,棱锥内有一点 到底面及各侧面的距离皆为1,则棱锥的体积为
到底面及各侧面的距离皆为1,则棱锥的体积为
您最近一年使用:0次
8 . 已知空间9点集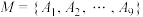 ,其中任意四点不共面.在这9个点间联结若干条线段,构成一个图G,使图中不存在四面体.问图G中最多有多少个三角形?
,其中任意四点不共面.在这9个点间联结若干条线段,构成一个图G,使图中不存在四面体.问图G中最多有多少个三角形?
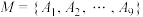 ,其中任意四点不共面.在这9个点间联结若干条线段,构成一个图G,使图中不存在四面体.问图G中最多有多少个三角形?
,其中任意四点不共面.在这9个点间联结若干条线段,构成一个图G,使图中不存在四面体.问图G中最多有多少个三角形?
您最近一年使用:0次
9 . 正三棱柱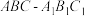 侧面六条对角线
侧面六条对角线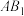 、
、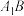 、
、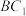 、
、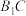 、
、 、
、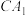 中,若有一对
中,若有一对 ,其余还有
,其余还有 对也互相垂直,则
对也互相垂直,则 等于( ).
等于( ).
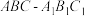 侧面六条对角线
侧面六条对角线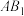 、
、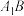 、
、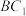 、
、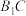 、
、 、
、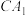 中,若有一对
中,若有一对 ,其余还有
,其余还有 对也互相垂直,则
对也互相垂直,则 等于( ).
等于( ).| A.2 |
| B.3 |
| C.4 |
| D.5 |
您最近一年使用:0次
名校
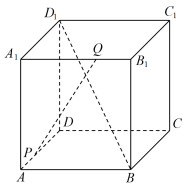
10 . 如图,在棱长为1的正方体 中,点
中,点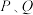 分别是棱
分别是棱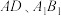 上的动点.若异面直线
上的动点.若异面直线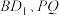 互相垂直,则
互相垂直,则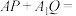
____ .
 中,点
中,点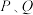 分别是棱
分别是棱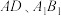 上的动点.若异面直线
上的动点.若异面直线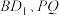 互相垂直,则
互相垂直,则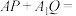

您最近一年使用:0次
2018-12-28更新
|
328次组卷
|
2卷引用:数学奥林匹克高中训练题(137)



