名校
1 . 已知函数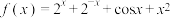 ,若
,若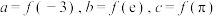 ,则( )
,则( )
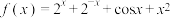 ,若
,若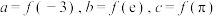 ,则( )
,则( )A.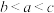 | B.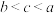 |
C. | D.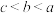 |
您最近一年使用:0次
2024-10-10更新
|
1382次组卷
|
3卷引用:福建省福州市闽侯县第一中学2024-2025学年高三上学期10月月考数学试题
名校
解题方法
2 . 已知定义在 上的偶函数
上的偶函数 和奇函数
和奇函数 满足
满足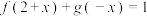 ,则( )
,则( )
 上的偶函数
上的偶函数 和奇函数
和奇函数 满足
满足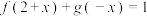 ,则( )
,则( )A. 的图象关于点 的图象关于点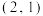 对称 对称 |
B. 是以8为周期的周期函数 是以8为周期的周期函数 |
C.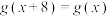 |
D.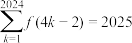 |
您最近一年使用:0次
2024-07-22更新
|
1819次组卷
|
6卷引用:福建省福州屏东中学2024-2025学年高三上学期10月适应性练习数学试题
名校
解题方法
3 . 已知 为双曲线
为双曲线 的左焦点,
的左焦点, 是
是 的右顶点,点
的右顶点,点 在过点
在过点 且斜率为
且斜率为 的直线上,
的直线上,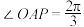 且线段
且线段 的垂直平分线经过点
的垂直平分线经过点 ,则
,则 的离心率为( )
的离心率为( )
 为双曲线
为双曲线 的左焦点,
的左焦点, 是
是 的右顶点,点
的右顶点,点 在过点
在过点 且斜率为
且斜率为 的直线上,
的直线上,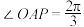 且线段
且线段 的垂直平分线经过点
的垂直平分线经过点 ,则
,则 的离心率为( )
的离心率为( )A. | B.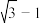 | C. | D. |
您最近一年使用:0次
2024-06-21更新
|
696次组卷
|
6卷引用:福建省福州第一中学2025届高三上学期10月月考数学试题
福建省福州第一中学2025届高三上学期10月月考数学试题云南省三校2025届高三高考备考实用性联考卷(一)数学试卷(已下线)模型23 圆锥曲线中有关三角形问题模型(第8章 解析几何)(已下线)第15题 双曲线中与半角有关的解三角形问题(一题多变)福建省福州市部分高中2024-2025学年高二上学期开学联考数学试题(已下线)3.2.2 双曲线的简单几何性质——课后作业(提升版)
名校
解题方法
4 . 若一个集合含有 个元素
个元素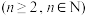 ,且这
,且这 个元素之和等于这
个元素之和等于这 个元素之积,则称该集合为
个元素之积,则称该集合为 元“复活集”.
元“复活集”.
(1)直接写出一个2元“复活集”(无需写出求解过程);
(2)求证:对任意一个2元“复活集”,若其元素均为正数,则其元素之积一定大于4;
(3)是否存在某个3元“复活集”,其元素均为正整数?若存在,求出所有符合条件的3元“复活集”;若不存在,说明理由.
 个元素
个元素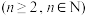 ,且这
,且这 个元素之和等于这
个元素之和等于这 个元素之积,则称该集合为
个元素之积,则称该集合为 元“复活集”.
元“复活集”.(1)直接写出一个2元“复活集”(无需写出求解过程);
(2)求证:对任意一个2元“复活集”,若其元素均为正数,则其元素之积一定大于4;
(3)是否存在某个3元“复活集”,其元素均为正整数?若存在,求出所有符合条件的3元“复活集”;若不存在,说明理由.
您最近一年使用:0次
7日内更新
|
116次组卷
|
2卷引用:福建省福州高级中学2024-2025学年高一上学期10月月考数学试卷
名校
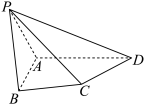
5 . 如图,在四棱锥 中,平面
中,平面 平面
平面 ,
, ,
,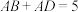 ,
,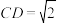 ,
,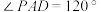 ,
, .
. 平面
平面 ;
;
(2)设 .
.
①若直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为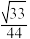 ,求线段
,求线段 的长.
的长.
②在线段 上是否存在点
上是否存在点 ,使得点
,使得点 ,
, ,
, 在以
在以 为球心的球上?若存在,求线段
为球心的球上?若存在,求线段 的长;若不存在,说明理由.
的长;若不存在,说明理由.
 中,平面
中,平面 平面
平面 ,
, ,
,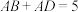 ,
,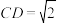 ,
,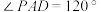 ,
, .
.
 平面
平面 ;
;(2)设
 .
.①若直线
 与平面
与平面 所成角的正弦值为
所成角的正弦值为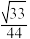 ,求线段
,求线段 的长.
的长.②在线段
 上是否存在点
上是否存在点 ,使得点
,使得点 ,
, ,
, 在以
在以 为球心的球上?若存在,求线段
为球心的球上?若存在,求线段 的长;若不存在,说明理由.
的长;若不存在,说明理由.
您最近一年使用:0次
7日内更新
|
577次组卷
|
8卷引用:福建省福州市部分学校教学联盟2024-2025学年高二上学期10月适应性检测数学试卷
福建省福州市部分学校教学联盟2024-2025学年高二上学期10月适应性检测数学试卷江苏省兴化中学2023-2024学年高二下学期期末适应性考试数学试题海南省儋州市第三中学2023-2024学年高二下学期数学期末复习考试试题(2)(已下线)数学02(新九省地区专用)-2025届新高三开学摸底考试卷福建省厦门市同安第一中学2024-2025学年高二上学期第一次月考(10月)数学试题黑龙江省绥化市青冈县哈尔滨师范大学青冈实验中学校2024-2025学年高二上学期10月考试数学试题山东省日照第一中学2024-2025学年高二上学期第一次质量检测数学试卷重庆市璧山来凤中学2024-2025学年高二上学期第一次月考(10月)数学试题
6 . 已知函数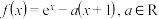 .
.
(1)讨论 的单调性;
的单调性;
(2)若 ,求曲线
,求曲线 在
在 处的切线方程;
处的切线方程;
(3)当 时,试讨论函数
时,试讨论函数 的零点个数.
的零点个数.
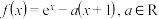 .
.(1)讨论
 的单调性;
的单调性;(2)若
 ,求曲线
,求曲线 在
在 处的切线方程;
处的切线方程;(3)当
 时,试讨论函数
时,试讨论函数 的零点个数.
的零点个数.
您最近一年使用:0次
7 . 如图正方体 中,点
中,点 是
是 的中点,点
的中点,点 为正方形
为正方形 内一动点,且
内一动点,且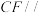 平面
平面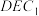 ,若异面直线
,若异面直线 与
与 所成角为
所成角为 ,则
,则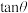 的最小值为
的最小值为_________ .
 中,点
中,点 是
是 的中点,点
的中点,点 为正方形
为正方形 内一动点,且
内一动点,且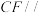 平面
平面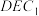 ,若异面直线
,若异面直线 与
与 所成角为
所成角为 ,则
,则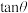 的最小值为
的最小值为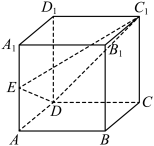
您最近一年使用:0次
名校
解题方法
8 . 已知函数 ,若对于任意的实数
,若对于任意的实数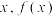 与
与 至少有一个为正数,则实数
至少有一个为正数,则实数 的取值范围是( )
的取值范围是( )
 ,若对于任意的实数
,若对于任意的实数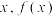 与
与 至少有一个为正数,则实数
至少有一个为正数,则实数 的取值范围是( )
的取值范围是( )A.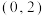 | B.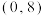 | C.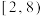 | D. |
您最近一年使用:0次
2024-09-22更新
|
1007次组卷
|
6卷引用:福建省福州屏东中学2024-2025学年高三上学期10月适应性练习数学试题
2024高二上·江苏·专题练习
名校
解题方法
9 . 设 ,过定点A的动直线
,过定点A的动直线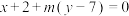 和过定点B的动直线
和过定点B的动直线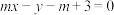 交于点
交于点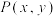 ,则
,则 的取值范围是
的取值范围是___________ .
 ,过定点A的动直线
,过定点A的动直线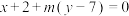 和过定点B的动直线
和过定点B的动直线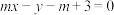 交于点
交于点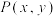 ,则
,则 的取值范围是
的取值范围是
您最近一年使用:0次
2024-09-19更新
|
2423次组卷
|
8卷引用:福建省福州市部分学校教学联盟2024-2025学年高二上学期10月适应性检测数学试卷
福建省福州市部分学校教学联盟2024-2025学年高二上学期10月适应性检测数学试卷(已下线)专题01 动直线的四种考法-【常考压轴题】(苏教版2019选择性必修第一册)江西省南昌市雷式学校&进贤县第一中学2024-2025学年高二上学期10月份联考数学试卷福建省厦门市双十中学2024-2025学年高二上学期第一次月考数学试卷甘肃省白银市第八中学2024-2025学年高二上学期第1次阶段性考试(10月)数学试题黑龙江省牡丹江市第一高级中学2024-2025学年高二上学期10月月考数学试题辽宁省师范大学附属中学2024-2025学年高二上学期10月模块考试数学试题山东省济宁市梁山县实验高级中学2024-2025学年高二上学期数学期中模拟题(一)
名校
解题方法
10 . 已知双曲线C: 的中心为O,离心率
的中心为O,离心率 ,点A在x轴上,
,点A在x轴上,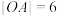 ,点P是C上一定点,P到x轴的距离为1,且
,点P是C上一定点,P到x轴的距离为1,且 .
.
(1)求双曲线C的方程;
(2)求C上任一点和A的距离的最小值;
(3)若C上的点M,N满足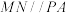 ,求证:在C上存在定点Q(异于P)使得P,M,N,Q在同一个圆上.
,求证:在C上存在定点Q(异于P)使得P,M,N,Q在同一个圆上.
 的中心为O,离心率
的中心为O,离心率 ,点A在x轴上,
,点A在x轴上,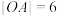 ,点P是C上一定点,P到x轴的距离为1,且
,点P是C上一定点,P到x轴的距离为1,且 .
.(1)求双曲线C的方程;
(2)求C上任一点和A的距离的最小值;
(3)若C上的点M,N满足
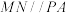 ,求证:在C上存在定点Q(异于P)使得P,M,N,Q在同一个圆上.
,求证:在C上存在定点Q(异于P)使得P,M,N,Q在同一个圆上.
您最近一年使用:0次



