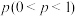名校
1 . 现有n枚质地不同的游戏币 ,向上抛出游戏币
,向上抛出游戏币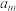 后,落下时正面朝上的概率为
后,落下时正面朝上的概率为 .甲、乙两人用这n枚游戏币玩游戏.
.甲、乙两人用这n枚游戏币玩游戏.
(1)甲将游戏币 向上抛出10次,用
向上抛出10次,用 表示落下时正面朝上的次数,求
表示落下时正面朝上的次数,求 的期望
的期望 ,并写出当
,并写出当 为何值时,
为何值时,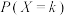 最大(直接写出结果,不用写过程);
最大(直接写出结果,不用写过程);
(2)甲将游戏币 向上抛出,用
向上抛出,用 表示落下时正面朝上游戏币的个数,求
表示落下时正面朝上游戏币的个数,求 的分布列;
的分布列;
(3)将这 枚游戏币依次向上抛出,规定若落下时正面朝上的个数为奇数,则甲获胜,否则乙获胜,请判断这个游戏规则是否公平,并说明理由.
枚游戏币依次向上抛出,规定若落下时正面朝上的个数为奇数,则甲获胜,否则乙获胜,请判断这个游戏规则是否公平,并说明理由.
 ,向上抛出游戏币
,向上抛出游戏币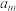 后,落下时正面朝上的概率为
后,落下时正面朝上的概率为 .甲、乙两人用这n枚游戏币玩游戏.
.甲、乙两人用这n枚游戏币玩游戏.(1)甲将游戏币
 向上抛出10次,用
向上抛出10次,用 表示落下时正面朝上的次数,求
表示落下时正面朝上的次数,求 的期望
的期望 ,并写出当
,并写出当 为何值时,
为何值时,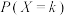 最大(直接写出结果,不用写过程);
最大(直接写出结果,不用写过程);(2)甲将游戏币
 向上抛出,用
向上抛出,用 表示落下时正面朝上游戏币的个数,求
表示落下时正面朝上游戏币的个数,求 的分布列;
的分布列;(3)将这
 枚游戏币依次向上抛出,规定若落下时正面朝上的个数为奇数,则甲获胜,否则乙获胜,请判断这个游戏规则是否公平,并说明理由.
枚游戏币依次向上抛出,规定若落下时正面朝上的个数为奇数,则甲获胜,否则乙获胜,请判断这个游戏规则是否公平,并说明理由.
您最近一年使用:0次
2024-09-07更新
|
742次组卷
|
5卷引用:重庆市第八中学校2024-2025学年高三上学期入学适应性训练数学试题
重庆市第八中学校2024-2025学年高三上学期入学适应性训练数学试题湖北省部分州市2025届高三上学期9月月考联合测评数学试题广西柳州高级中学2024-2025学年高三上学期9月自主综合考试数学试题山西省晋城市第一中学校2025届高三上学期第五次调研考试(9月)数学试题(已下线)第08讲 两点分布、二项分布、超几何分布与正态分布(十一大题型)(讲义)-1
名校
2 . 已知函数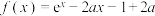 ・
・
(1)若 ,讨论
,讨论 的单调性;
的单调性;
(2)若 ,已知函数
,已知函数 ,若
,若 恒成立,求
恒成立,求 的取值范围.
的取值范围.
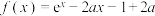 ・
・(1)若
 ,讨论
,讨论 的单调性;
的单调性;(2)若
 ,已知函数
,已知函数 ,若
,若 恒成立,求
恒成立,求 的取值范围.
的取值范围.
您最近一年使用:0次
2024-09-07更新
|
1036次组卷
|
4卷引用:重庆市第八中学校2024-2025学年高三上学期入学适应性训练数学试题
名校
解题方法
3 . 某趣味活动设置了“谜语竞猜”和“知识竞答”两个环节,小王参与这两个环节的活动.
在“谜语竞猜”环节,设置①、②、③三道谜语题,猜谜者按照一定的顺序猜谜,只有猜对当前谜语才能继续竞猜下一道谜语,并且获得本谜语的奖金.每次猜谜的结果相互独立.猜对三道谜语的概率及获得的相应奖金如下表:
(1)若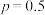 ,按“①、②、③”的顺序猜谜.在所获奖金不低于10元的条件下,求小王所获奖金为30元的概率;
,按“①、②、③”的顺序猜谜.在所获奖金不低于10元的条件下,求小王所获奖金为30元的概率;
(2)假设只按“①、②、③”和“③、②、①”两种顺序猜谜.若以猜谜所获奖金的数学期望为决策依据,小王应按哪种顺序猜谜所获奖金更多?
(3)在“知识竞答环节,参赛者要回答A、B两类问题,每个参赛者回答n次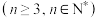 ,每次回答一个问题,若回答正确,则下一个问题从B类中随机抽取;若回答错误,则下一个问题从A类中随机抽取,规定每位参赛者回答的第一个问题从A类中抽取.已知小王能正确回答A类问题的概率为
,每次回答一个问题,若回答正确,则下一个问题从B类中随机抽取;若回答错误,则下一个问题从A类中随机抽取,规定每位参赛者回答的第一个问题从A类中抽取.已知小王能正确回答A类问题的概率为 ,能正确回答B类问题的概率为
,能正确回答B类问题的概率为 ,且每次回答问题正确与否相互独立,求小王第n次回答正确的概率
,且每次回答问题正确与否相互独立,求小王第n次回答正确的概率 .
.
在“谜语竞猜”环节,设置①、②、③三道谜语题,猜谜者按照一定的顺序猜谜,只有猜对当前谜语才能继续竞猜下一道谜语,并且获得本谜语的奖金.每次猜谜的结果相互独立.猜对三道谜语的概率及获得的相应奖金如下表:
谜语 | ① | ② | ③ |
猜对的概率 | 0.8 |
| 0.5 |
获得的奖金(元) | 10 | 20 | 30 |
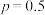 ,按“①、②、③”的顺序猜谜.在所获奖金不低于10元的条件下,求小王所获奖金为30元的概率;
,按“①、②、③”的顺序猜谜.在所获奖金不低于10元的条件下,求小王所获奖金为30元的概率;(2)假设只按“①、②、③”和“③、②、①”两种顺序猜谜.若以猜谜所获奖金的数学期望为决策依据,小王应按哪种顺序猜谜所获奖金更多?
(3)在“知识竞答环节,参赛者要回答A、B两类问题,每个参赛者回答n次
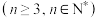 ,每次回答一个问题,若回答正确,则下一个问题从B类中随机抽取;若回答错误,则下一个问题从A类中随机抽取,规定每位参赛者回答的第一个问题从A类中抽取.已知小王能正确回答A类问题的概率为
,每次回答一个问题,若回答正确,则下一个问题从B类中随机抽取;若回答错误,则下一个问题从A类中随机抽取,规定每位参赛者回答的第一个问题从A类中抽取.已知小王能正确回答A类问题的概率为 ,能正确回答B类问题的概率为
,能正确回答B类问题的概率为 ,且每次回答问题正确与否相互独立,求小王第n次回答正确的概率
,且每次回答问题正确与否相互独立,求小王第n次回答正确的概率 .
.
您最近一年使用:0次
名校
4 . 在 中,
中, ,
,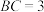 ,
, ,
, 分别是
分别是 上的点,满足
上的点,满足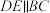 且
且 经过
经过 的重心,将
的重心,将 沿
沿 折起到
折起到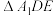 的位置,使
的位置,使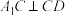 ,
, 是
是 的中点,如图所示.
的中点,如图所示.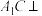 平面
平面 ;
;
(2)求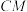 与平面
与平面 所成角的大小;
所成角的大小;
(3)在线段 上是否存在点
上是否存在点 ,使平面
,使平面 与平面
与平面 成角余弦值为
成角余弦值为 ?若存在,求出
?若存在,求出 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
 中,
中, ,
,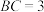 ,
, ,
, 分别是
分别是 上的点,满足
上的点,满足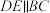 且
且 经过
经过 的重心,将
的重心,将 沿
沿 折起到
折起到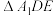 的位置,使
的位置,使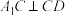 ,
, 是
是 的中点,如图所示.
的中点,如图所示.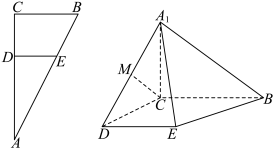
 平面
平面 ;
;(2)求
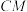 与平面
与平面 所成角的大小;
所成角的大小;(3)在线段
 上是否存在点
上是否存在点 ,使平面
,使平面 与平面
与平面 成角余弦值为
成角余弦值为 ?若存在,求出
?若存在,求出 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
您最近一年使用:0次
2024-07-18更新
|
2497次组卷
|
16卷引用:重庆市巴蜀中学校2024-2025学年高二上学期开学考试数学试卷(B)
重庆市巴蜀中学校2024-2025学年高二上学期开学考试数学试卷(B)福建省九地市部分学校2024-2025学年高二上学期开学质量检测数学试卷吉林省普通高中G6教考联盟2023-2024学年高一下学期7月期末考试数学试题(已下线)第3题 由二面角求参数(一题多解)(已下线)压轴题06 空间向量与立体几何4大类型专练-【常考压轴题】(人教B版2019选择性必修第一册)山东省北镇中学2024-2025学年高二上学期第二次考试(9月月考)数学试题(已下线)模块三 较难第1套 模拟卷(高二期中备考模拟)四川省成都市新津中学2024-2025学年高二上学期10月月考数学试题陕西省咸阳市乾县晨光中学2024-2025学年高二上学期第二次阶段性测试数学试卷福建省部分学校教学联盟2024-2025学年高二上学期10月月考数学试题山东省青岛第十七中学2024-2025学年高二上学期第一次月考数学试题广东省佛山市顺德区北滘中学2024-2025学年高二上学期10月月考数学试题山东省济钢高级中学2024-2025学年高二上学期第一次学情检测数学试题四川省广安市第二中学2024-2025学年高二上学期第一次月考数学试题山东省淄博第六中学2024-2025学年高二上学期第一次单元检测数学试卷山西省阳泉市第一中学2024-2025学年高二上学期10月月考数学试题
5 . 已知动点 与定点
与定点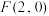 的距离和
的距离和 到定直线
到定直线 的距离的比是常数
的距离的比是常数 ,记
,记 的轨迹为
的轨迹为 .
.
(1)求 的方程;
的方程;
(2)过原点 的直线交
的直线交 于
于 两点,过
两点,过 作直线
作直线 的垂线交
的垂线交 于点
于点 (异于点
(异于点 ),直线
),直线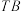 与
与 轴,
轴, 轴分别交于点
轴分别交于点 .设直线
.设直线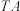 ,
,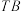 的斜率分别为
的斜率分别为 ,
, .
.
(ⅰ)证明: 为定值;
为定值;
(ⅱ)求四边形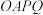 面积的最大值.
面积的最大值.
 与定点
与定点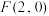 的距离和
的距离和 到定直线
到定直线 的距离的比是常数
的距离的比是常数 ,记
,记 的轨迹为
的轨迹为 .
.(1)求
 的方程;
的方程;(2)过原点
 的直线交
的直线交 于
于 两点,过
两点,过 作直线
作直线 的垂线交
的垂线交 于点
于点 (异于点
(异于点 ),直线
),直线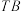 与
与 轴,
轴, 轴分别交于点
轴分别交于点 .设直线
.设直线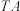 ,
,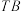 的斜率分别为
的斜率分别为 ,
, .
.(ⅰ)证明:
 为定值;
为定值;(ⅱ)求四边形
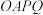 面积的最大值.
面积的最大值.
您最近一年使用:0次
2024-07-10更新
|
418次组卷
|
4卷引用:重庆市巴蜀科学城中学2024-2025学年高二上学期入学测试数学试题
重庆市巴蜀科学城中学2024-2025学年高二上学期入学测试数学试题福建省厦门市2023-2024学年高二下学期期末质量检测数学试题(已下线)压轴题08 圆锥曲线综合的5大常考类型-【常考压轴题】(人教B版2019选择性必修第一册)(已下线)专题3 圆锥曲线中的最值与范围问题【讲】(高二期中压轴专项)
名校
解题方法
6 . 在矩形 中,
中, ,
, ,
, 为矩形
为矩形 所在平面内的动点,且
所在平面内的动点,且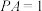 ,则
,则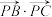 的最大值是( )
的最大值是( )
 中,
中, ,
, ,
, 为矩形
为矩形 所在平面内的动点,且
所在平面内的动点,且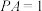 ,则
,则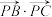 的最大值是( )
的最大值是( )| A.9 | B.10 | C.11 | D.12 |
您最近一年使用:0次
2024-07-07更新
|
1073次组卷
|
4卷引用:重庆市巴蜀中学校2024-2025学年高二上学期开学考试数学试卷(B)
重庆市巴蜀中学校2024-2025学年高二上学期开学考试数学试卷(B)北京市昌平区2023-2024学年高一下学期期末质量抽测数学试卷(已下线)拔高点突破01 一网打尽平面向量中的范围与最值问题(十大题型)-2(已下线)重难点突破01 圆中的范围与最值问题(八大题型)
名校
解题方法
7 . 已知 ,
, 是椭圆
是椭圆 的左、右焦点,若椭圆上总存在点
的左、右焦点,若椭圆上总存在点 ,使得
,使得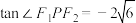 ,则椭圆的离心率的取值范围为( )
,则椭圆的离心率的取值范围为( )
 ,
, 是椭圆
是椭圆 的左、右焦点,若椭圆上总存在点
的左、右焦点,若椭圆上总存在点 ,使得
,使得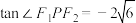 ,则椭圆的离心率的取值范围为( )
,则椭圆的离心率的取值范围为( )A. | B.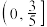 | C. | D.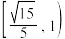 |
您最近一年使用:0次
2024-07-04更新
|
1144次组卷
|
3卷引用:重庆市巴蜀科学城中学2024-2025学年高二上学期入学测试数学试题
重庆市巴蜀科学城中学2024-2025学年高二上学期入学测试数学试题重庆市第一中学校2023-2024学年高一下学期期末考试数学试题(已下线)压轴题08 圆锥曲线综合的5大常考类型-【常考压轴题】(人教B版2019选择性必修第一册)
名校
8 . 已知函数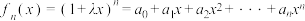 ,其中
,其中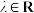 ,
, .
.
(1)若 ,
,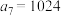 ,求
,求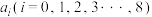 的最大值;
的最大值;
(2)若 ,求
,求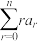 ;(用
;(用 表示)
表示)
(3)若 ,求
,求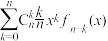
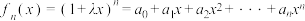 ,其中
,其中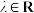 ,
, .
.(1)若
 ,
,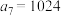 ,求
,求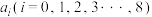 的最大值;
的最大值;(2)若
 ,求
,求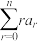 ;(用
;(用 表示)
表示)(3)若
 ,求
,求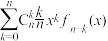
您最近一年使用:0次
名校
9 . 设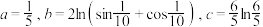 ,则
,则 的大小关系是( )
的大小关系是( )
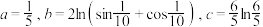 ,则
,则 的大小关系是( )
的大小关系是( )A.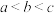 | B.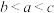 | C. | D.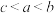 |
您最近一年使用:0次
2024-05-29更新
|
1322次组卷
|
5卷引用:重庆市南开中学2025届高三上学期8月第一次质量检测数学试题
名校
10 . 在棱长为 1 的正方体 中,已知
中,已知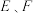 分别为线段
分别为线段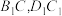 的中点,点
的中点,点 满足
满足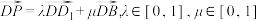 ,则( )
,则( )
 中,已知
中,已知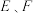 分别为线段
分别为线段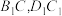 的中点,点
的中点,点 满足
满足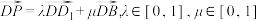 ,则( )
,则( )A.当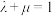 时,三棱锥 时,三棱锥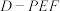 的体积为定值 的体积为定值 |
B.当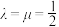 ,四棱锥 ,四棱锥 的外接球的表面积是 的外接球的表面积是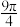 |
C. 周长的最小值为 周长的最小值为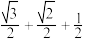 |
D.若 ,则点 ,则点 的轨迹长为 的轨迹长为 |
您最近一年使用:0次
2024-05-25更新
|
1313次组卷
|
5卷引用:重庆市万州第二高级中学2024-2025学年高二上学期入学考试数学检测试卷