名校
解题方法
1 . 在 中,角
中,角 为锐角,
为锐角, 的面积为
的面积为 ,且
,且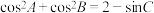 ,则
,则 周长的最小值为( )
周长的最小值为( )
 中,角
中,角 为锐角,
为锐角, 的面积为
的面积为 ,且
,且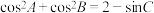 ,则
,则 周长的最小值为( )
周长的最小值为( )A.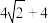 | B.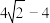 | C.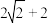 | D.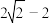 |
您最近一年使用:0次
7日内更新
|
205次组卷
|
3卷引用:甘肃省张掖市部分学校2025届高三上学期10月质量检测数学试卷
名校
解题方法
2 . 已知双曲线 的渐近线为
的渐近线为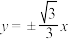 ,左顶点为
,左顶点为 .
.
(1)求双曲线 的方程;
的方程;
(2)直线 交
交 轴于点
轴于点 ,过
,过 点的直线交双曲线
点的直线交双曲线 于
于 ,
, ,直线
,直线 ,
, 分别交
分别交 于
于 ,
, ,若
,若 ,
, ,
, ,
, 均在圆
均在圆 上,
上,
①求 的值,并求点
的值,并求点 的横坐标;
的横坐标;
②求圆 面积的取值范围.
面积的取值范围.
 的渐近线为
的渐近线为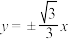 ,左顶点为
,左顶点为 .
.(1)求双曲线
 的方程;
的方程;(2)直线
 交
交 轴于点
轴于点 ,过
,过 点的直线交双曲线
点的直线交双曲线 于
于 ,
, ,直线
,直线 ,
, 分别交
分别交 于
于 ,
, ,若
,若 ,
, ,
, ,
, 均在圆
均在圆 上,
上,①求
 的值,并求点
的值,并求点 的横坐标;
的横坐标;②求圆
 面积的取值范围.
面积的取值范围.
您最近一年使用:0次
名校
解题方法
3 . 泰勒公式是一个非常重要的数学定理,它可以将一个函数在某一点处展开成无限项的多项式.当 在
在 处的
处的 阶导数都存在时,它的公式表达式如下:
阶导数都存在时,它的公式表达式如下: .注:
.注: 表示函数
表示函数 在原点处的一阶导数,
在原点处的一阶导数, 表示在原点处的二阶导数,以此类推,
表示在原点处的二阶导数,以此类推, 表示在原点处的
表示在原点处的 阶导数.
阶导数.
(1)根据公式估算 的值,精确到小数点后两位;
的值,精确到小数点后两位;
(2)当 时,比较
时,比较 与
与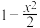 的大小,并证明;
的大小,并证明;
(3)设 ,证明:
,证明: .
.
 在
在 处的
处的 阶导数都存在时,它的公式表达式如下:
阶导数都存在时,它的公式表达式如下: .注:
.注: 表示函数
表示函数 在原点处的一阶导数,
在原点处的一阶导数, 表示在原点处的二阶导数,以此类推,
表示在原点处的二阶导数,以此类推, 表示在原点处的
表示在原点处的 阶导数.
阶导数.(1)根据公式估算
 的值,精确到小数点后两位;
的值,精确到小数点后两位;(2)当
 时,比较
时,比较 与
与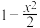 的大小,并证明;
的大小,并证明;(3)设
 ,证明:
,证明: .
.
您最近一年使用:0次
2024-05-23更新
|
652次组卷
|
3卷引用:甘肃省张掖市某校2023-2024学年高三下学期模拟考试数学试题
甘肃省张掖市某校2023-2024学年高三下学期模拟考试数学试题河北省衡水市第二中学2023-2024学年高二下学期6月期末素养评估数学试题(已下线)专题7 以新定义为背景的相关问题【讲】(高二期末压轴专项)
名校
解题方法
4 . 已知函数 及其导函数
及其导函数 的定义域均为
的定义域均为 .设
.设 ,曲线
,曲线 在点
在点 处的切线交
处的切线交 轴于点
轴于点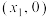 .当
.当 时,设曲线
时,设曲线 在点
在点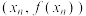 处的切线交
处的切线交 轴于点
轴于点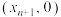 .依此类推,称得到的数列
.依此类推,称得到的数列 为函数
为函数 关于
关于 的“
的“ 数列”.
数列”.
(1)若 ,
, 是函数
是函数 关于
关于 的“
的“ 数列”,求
数列”,求 的值;
的值;
(2)若 ,
, 是函数
是函数 关于
关于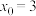 的“
的“ 数列”,记
数列”,记 ,证明:
,证明: 是等比数列,并求出其公比;
是等比数列,并求出其公比;
(3)若 ,则对任意给定的非零实数
,则对任意给定的非零实数 ,是否存在
,是否存在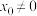 ,使得函数
,使得函数 关于
关于 的“
的“ 数列”
数列” 为周期数列?若存在,求出所有满足条件的
为周期数列?若存在,求出所有满足条件的 ;若不存在,请说明理由.
;若不存在,请说明理由.
 及其导函数
及其导函数 的定义域均为
的定义域均为 .设
.设 ,曲线
,曲线 在点
在点 处的切线交
处的切线交 轴于点
轴于点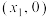 .当
.当 时,设曲线
时,设曲线 在点
在点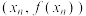 处的切线交
处的切线交 轴于点
轴于点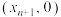 .依此类推,称得到的数列
.依此类推,称得到的数列 为函数
为函数 关于
关于 的“
的“ 数列”.
数列”.(1)若
 ,
, 是函数
是函数 关于
关于 的“
的“ 数列”,求
数列”,求 的值;
的值;(2)若
 ,
, 是函数
是函数 关于
关于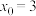 的“
的“ 数列”,记
数列”,记 ,证明:
,证明: 是等比数列,并求出其公比;
是等比数列,并求出其公比;(3)若
 ,则对任意给定的非零实数
,则对任意给定的非零实数 ,是否存在
,是否存在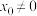 ,使得函数
,使得函数 关于
关于 的“
的“ 数列”
数列” 为周期数列?若存在,求出所有满足条件的
为周期数列?若存在,求出所有满足条件的 ;若不存在,请说明理由.
;若不存在,请说明理由.
您最近一年使用:0次
2024-04-01更新
|
971次组卷
|
6卷引用:甘肃省张掖市某校2024届高三下学期第三次模拟数学试卷
甘肃省张掖市某校2024届高三下学期第三次模拟数学试卷上海市浦东新区2024届高三下学期期中教学质量检测数学试卷(已下线)数学(上海卷02)(已下线)专题09 导数及其应用 压轴题(六大题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(沪教版2020选择性必修,上海专用)广东省东莞中学、广州二中、惠州一中、深圳实验、珠海一中、中山纪念中学2024届高三下学期第五次六校联考数学试题(已下线)专题3 数列中的新定义压轴大题(过关集训)
名校
5 . 已知函数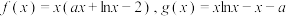 ,
,
(1)若 与
与 有相同的单调区间,求实数
有相同的单调区间,求实数 的值;
的值;
(2)若方程 有两个不同的实根
有两个不同的实根 ,证明:
,证明: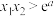 .
.
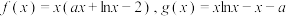 ,
,(1)若
 与
与 有相同的单调区间,求实数
有相同的单调区间,求实数 的值;
的值;(2)若方程
 有两个不同的实根
有两个不同的实根 ,证明:
,证明: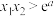 .
.
您最近一年使用:0次
2024-03-22更新
|
833次组卷
|
4卷引用:甘肃省张掖市某校2024届高三下学期模拟考试数学试题
甘肃省张掖市某校2024届高三下学期模拟考试数学试题四川省成都外国语学校2024届高三下学期高考模拟(二)数学(理科)试题(已下线)专题1 导数与函数的单调性(恒单调、存在单调区间、不单调)【练】四川省雅安市神州天立学校2024届高三下学期高考冲刺热身(四)数学(理)试题
名校
6 . 某制药公司研制了一款针对某种病毒的新疫苗.该病毒一般通过病鼠与白鼠之间的接触传染,现有 只白鼠,每只白鼠在接触病鼠后被感染的概率为
只白鼠,每只白鼠在接触病鼠后被感染的概率为 ,被感染的白鼠数用随机变量X表示,假设每只白鼠是否被感染之间相互独立
,被感染的白鼠数用随机变量X表示,假设每只白鼠是否被感染之间相互独立
(1)若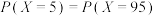 ,求数学期望
,求数学期望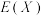 ;
;
(2)接种疫苗后的白鼠被病鼠感染的概率为 ,现有两个不同的研究团队理论研究发现概率
,现有两个不同的研究团队理论研究发现概率 与参数
与参数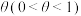 的取值有关.团队A提出函数模型为
的取值有关.团队A提出函数模型为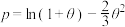 ,团队B提出函数模型为
,团队B提出函数模型为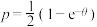 .现将100只接种疫苗后的白鼠分成10组,每组10只,进行实验,随机变量
.现将100只接种疫苗后的白鼠分成10组,每组10只,进行实验,随机变量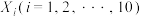 表示第
表示第 组被感染的白鼠数,将随机变量
组被感染的白鼠数,将随机变量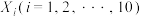 的实验结果
的实验结果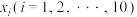 绘制成频数分布图,如图所示.
绘制成频数分布图,如图所示. ”发生的概率表达式(用
”发生的概率表达式(用 表示,组合数不必计算);
表示,组合数不必计算);
(ⅱ)在统计学中,若参数 时使得概率
时使得概率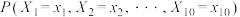 最大,称
最大,称 是
是 的最大似然估计.根据这一原理和团队A,B提出的函数模型,判断哪个团队的函数模型可以求出
的最大似然估计.根据这一原理和团队A,B提出的函数模型,判断哪个团队的函数模型可以求出 的最大似然估计,并求出最大似然估计.参考数据:
的最大似然估计,并求出最大似然估计.参考数据: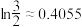 .
.
 只白鼠,每只白鼠在接触病鼠后被感染的概率为
只白鼠,每只白鼠在接触病鼠后被感染的概率为 ,被感染的白鼠数用随机变量X表示,假设每只白鼠是否被感染之间相互独立
,被感染的白鼠数用随机变量X表示,假设每只白鼠是否被感染之间相互独立(1)若
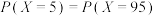 ,求数学期望
,求数学期望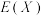 ;
;(2)接种疫苗后的白鼠被病鼠感染的概率为
 ,现有两个不同的研究团队理论研究发现概率
,现有两个不同的研究团队理论研究发现概率 与参数
与参数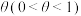 的取值有关.团队A提出函数模型为
的取值有关.团队A提出函数模型为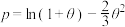 ,团队B提出函数模型为
,团队B提出函数模型为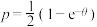 .现将100只接种疫苗后的白鼠分成10组,每组10只,进行实验,随机变量
.现将100只接种疫苗后的白鼠分成10组,每组10只,进行实验,随机变量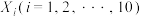 表示第
表示第 组被感染的白鼠数,将随机变量
组被感染的白鼠数,将随机变量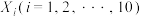 的实验结果
的实验结果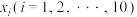 绘制成频数分布图,如图所示.
绘制成频数分布图,如图所示.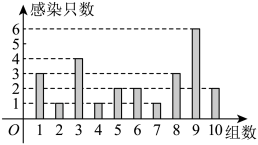
 ”发生的概率表达式(用
”发生的概率表达式(用 表示,组合数不必计算);
表示,组合数不必计算);(ⅱ)在统计学中,若参数
 时使得概率
时使得概率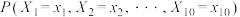 最大,称
最大,称 是
是 的最大似然估计.根据这一原理和团队A,B提出的函数模型,判断哪个团队的函数模型可以求出
的最大似然估计.根据这一原理和团队A,B提出的函数模型,判断哪个团队的函数模型可以求出 的最大似然估计,并求出最大似然估计.参考数据:
的最大似然估计,并求出最大似然估计.参考数据: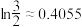 .
.
您最近一年使用:0次
2024-02-23更新
|
1889次组卷
|
10卷引用:甘肃省张掖市某校2024届高三下学期第三次模拟数学试卷
甘肃省张掖市某校2024届高三下学期第三次模拟数学试卷浙江省9+1高中联盟2022-2023学年高二下学期期中数学试题(已下线)广东省深圳中学2023届高三5月适应性测试数学试题湖南省长沙市雅礼中学2023-2024学年高三上学期月考(五)(1月期末)数学试卷辽宁省沈阳市东北育才学校高中部2023-2024学年高三第六次模拟考试暨假期质量测试数学试题辽宁省八市八校2024届度高三第二次联合模拟考试数学试题浙江省余姚中学2023-2024学年高二下学期期中考试数学试题广东省八校2024-2025学年高三上学期9月联合检测数学试卷(已下线)第五章 概率统计创新问题 专题一 概率统计决策问题 微点3 概率统计决策问题综合训练【培优版】(已下线)第五章 概率统计创新问题 专题七 概率统计中的新定义问题 微点4 概率统计中的新定义问题(四)【培优版】
名校
解题方法
7 . 已知数列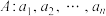 为有穷正整数数列.若数列A满足如下两个性质,则称数列A为m的k减数列:
为有穷正整数数列.若数列A满足如下两个性质,则称数列A为m的k减数列:
①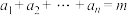 ;
;
②对于 ,使得
,使得 的正整数对
的正整数对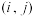 有k个.
有k个.
(1)写出所有4的1减数列;
(2)若存在m的6减数列,证明: ;
;
(3)若存在2024的k减数列,求k的最大值.
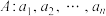 为有穷正整数数列.若数列A满足如下两个性质,则称数列A为m的k减数列:
为有穷正整数数列.若数列A满足如下两个性质,则称数列A为m的k减数列:①
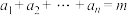 ;
;②对于
 ,使得
,使得 的正整数对
的正整数对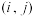 有k个.
有k个.(1)写出所有4的1减数列;
(2)若存在m的6减数列,证明:
 ;
;(3)若存在2024的k减数列,求k的最大值.
您最近一年使用:0次
2024-01-25更新
|
4194次组卷
|
10卷引用:甘肃省张掖市2023-2024学年高三下学期第三次诊断考试数学试卷
名校
8 . 已知函数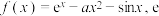 为自然对数的底数
为自然对数的底数
(1)求 在
在 处的切线方程;
处的切线方程;
(2)当 时,
时, ,求实数
,求实数 的最大值;
的最大值;
(3)证明:当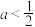 时,
时, 在
在 处取极小值.
处取极小值.
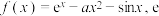 为自然对数的底数
为自然对数的底数(1)求
 在
在 处的切线方程;
处的切线方程;(2)当
 时,
时, ,求实数
,求实数 的最大值;
的最大值;(3)证明:当
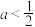 时,
时, 在
在 处取极小值.
处取极小值.
您最近一年使用:0次
2022-02-02更新
|
1712次组卷
|
4卷引用:甘肃省张掖市某重点校2022-2023学年高三上学期第九次检测数学(理)试题
名校
9 . 已知函数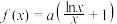 ,(其中a为非零实数).
,(其中a为非零实数).
(1)讨论 的单调性;
的单调性;
(2)若函数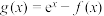 (e为自然对数的底数)有两个零点.
(e为自然对数的底数)有两个零点.
①求实数a的取值范围;
②设两个零点分别为 、
、 ,求证:
,求证: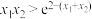 .
.
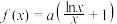 ,(其中a为非零实数).
,(其中a为非零实数).(1)讨论
 的单调性;
的单调性;(2)若函数
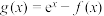 (e为自然对数的底数)有两个零点.
(e为自然对数的底数)有两个零点.①求实数a的取值范围;
②设两个零点分别为
 、
、 ,求证:
,求证: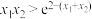 .
.
您最近一年使用:0次
2021-12-08更新
|
1982次组卷
|
10卷引用:甘肃省张掖市2021-2022学年高三第二次全市联考(3月)理科数学试题
甘肃省张掖市2021-2022学年高三第二次全市联考(3月)理科数学试题湖南省炎德英才2022届高三上学期12月联考数学试题重庆市南开中学2022届高三上学期12月月考数学试题湖南省名校联合体2021-2022学年高三上学期12月联考数学试题(已下线)专题05 导数与函数的零点问题(练)--第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测(新高考·全国卷)》湖南师范大学附属中学2021-2022学年高三上学期12月联考数学试题(已下线)专题3-2 含参讨论-2022年高考数学毕业班二轮热点题型归纳与变式演练(全国通用)安徽省滁州市定远县育才学校2023届高三上学期期末数学试题江苏省扬州市邗江中学2021-2022学年高二上学期期末模拟数学试题(已下线)第八章 利用导数证明不等式专题八 帕德逼近与不等式的证明 微点2 帕德逼近与不等式的证明综合训练
名校
解题方法
10 . 已知函数 的导函数
的导函数 满足:
满足: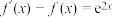 ,且
,且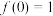 ,当
,当 时,
时,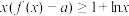 恒成立,则实数a的取值范围是
恒成立,则实数a的取值范围是______________ .
 的导函数
的导函数 满足:
满足: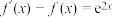 ,且
,且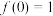 ,当
,当 时,
时,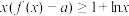 恒成立,则实数a的取值范围是
恒成立,则实数a的取值范围是
您最近一年使用:0次
2021-11-29更新
|
2174次组卷
|
11卷引用:甘肃省民乐县第一中学2021-2022学年上学期高三第二次诊断(12月)考试数学(理)试题
甘肃省民乐县第一中学2021-2022学年上学期高三第二次诊断(12月)考试数学(理)试题重庆市第一中学2022届高三上学期期中数学试题(已下线)专题03 利用导数解不等式与不等式恒成立问题(练)--第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测(新高考·全国卷)》湖南省长沙市第一中学2022届高三下学期月考(七)数学试题江西省(东乡一中、都昌一中、丰城中学、赣州中学、景德镇二中、上饶中学、上栗中学、新建二中)新八校2022届高三下学期第二次联考数学(理)试题广东省深圳外国语学校(集团)2023届高三上学期第一次月考数学试题湖南省邵阳市第二中学2022-2023学年高三上学期7月阶段性考试(三)数学试题山东省济宁市育才中学2022-2023学年高三上学期开学数学试题(已下线)专题04 盘点处理不等式恒成立的六种方法-2(已下线)第六章 导数与不等式恒成立问题 专题一 两类经典不等式 微点2 两个重要的对数不等式广东省广州市育才中学2023-2024学年高二下学期期中数学试题



