1 . 《几何原本》是古希腊数学家欧几里得得所著的一部数学著作,在《几何原本》第六卷给出了内角平分线定理,其内容为:在一个三角形中,三角形一个内角的角平分线内分对边所成的两条线段,与这个角的两邻边对应成比例.例如,在 中(图1),
中(图1), 为
为 的平分线,则有
的平分线,则有 .
.
(2)如图2,已知 的重心为
的重心为 ,内心为
,内心为 ,若
,若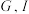 的连线
的连线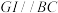 .求证:
.求证: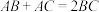 .
.
 中(图1),
中(图1), 为
为 的平分线,则有
的平分线,则有 .
.
(2)如图2,已知
 的重心为
的重心为 ,内心为
,内心为 ,若
,若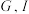 的连线
的连线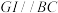 .求证:
.求证: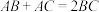 .
.
您最近一年使用:0次
2 . 固定项链的两端,在重力的作用下项链所形成的曲线是悬链线.1691年,莱布尼茨等得出“悬链线”方程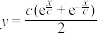 ,其中
,其中 为参数.当
为参数.当 时,就是双曲余弦函数
时,就是双曲余弦函数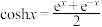 ,类似地我们可以定义双曲正弦函数
,类似地我们可以定义双曲正弦函数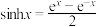 .它们与正、余弦函数有许多类似的性质.
.它们与正、余弦函数有许多类似的性质.
(1)类比正弦函数的二倍角公式,请写出双曲正弦函数的一个正确的结论: _____________.(只写出即可,不要求证明);
_____________.(只写出即可,不要求证明);
(2)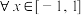 ,不等式
,不等式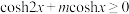 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)若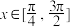 ,试比较
,试比较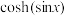 与
与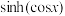 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
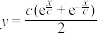 ,其中
,其中 为参数.当
为参数.当 时,就是双曲余弦函数
时,就是双曲余弦函数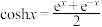 ,类似地我们可以定义双曲正弦函数
,类似地我们可以定义双曲正弦函数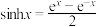 .它们与正、余弦函数有许多类似的性质.
.它们与正、余弦函数有许多类似的性质.(1)类比正弦函数的二倍角公式,请写出双曲正弦函数的一个正确的结论:
 _____________.(只写出即可,不要求证明);
_____________.(只写出即可,不要求证明);(2)
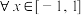 ,不等式
,不等式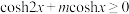 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(3)若
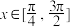 ,试比较
,试比较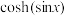 与
与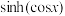 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
您最近一年使用:0次
2024-01-27更新
|
913次组卷
|
8卷引用:福建省宁德市2023-2024学年高一上学期1月期末质量检测数学试题
福建省宁德市2023-2024学年高一上学期1月期末质量检测数学试题重庆市缙云教育联盟2024届高三下学期2月月度质量检测数学试题(已下线)压轴题函数与导数新定义题(九省联考第19题模式)讲河南省名校联盟2023-2024学年高一下学期3月测试数学试题(已下线)第八章:向量的数量积与三角恒等变换章末重点题型复习(2)-同步精品课堂(人教B版2019必修第三册)河南省信阳市信阳高级中学2023-2024学年高一下学期3月月考(一)数学试题(已下线)第8章:向量的数量积与三角恒等变换章末综合检测卷(新题型)-【帮课堂】(人教B版2019必修第三册)(已下线)专题04 三角函数恒等变形综合大题归类 -期末考点大串讲(苏教版(2019))
名校
3 . 《见微知著》谈到:从一个简单的经典问题出发,从特殊到一般,由简单到复杂:从部分到整体,由低维到高维,知识与方法上的类比是探索发展的重要途径,是思想阀门发现新问题、新结论的重要方法,
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察;(2)整体设元;(3)整体代入:(4)整体求和等.
例如, ,求证:
,求证: .
.
证明:原式 .
.
波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.
请根据阅读材料解答下列问题
(1)已知如 ,求
,求 ___________.
___________.
(2)若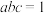 ,解方程
,解方程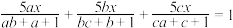 .
.
(3)若正数 、
、 满足
满足 ,求
,求 的最小值.
的最小值.
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察;(2)整体设元;(3)整体代入:(4)整体求和等.
例如,
 ,求证:
,求证: .
.证明:原式
 .
.波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.
请根据阅读材料解答下列问题
(1)已知如
 ,求
,求 ___________.
___________.(2)若
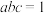 ,解方程
,解方程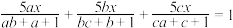 .
.(3)若正数
 、
、 满足
满足 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次
2023-10-17更新
|
215次组卷
|
2卷引用:重庆市第十一中学校2023-2024学年高一上学期10月月考数学试题
名校
4 . 《见微知著》谈到:从一个简单的经典问题出发,从特殊到一般,由简单到复杂:从部分到整体,由低维到高维,知识与方法上的类比是探索发展的重要途径,是思想阀门发现新问题、新结论的重要方法.
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察;(2)整体设元;(3)整体代入;(4)整体求和等.
例如, ,求证:
,求证: .
.
证明:原式 .
.
波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.
阅读材料二:基本不等式 ,当且仅当
,当且仅当 时等号成立,它是解决最值问题的有力工具.
时等号成立,它是解决最值问题的有力工具.
例如:在 的条件下,当x为何值时,
的条件下,当x为何值时, 有最小值,最小值是多少?
有最小值,最小值是多少?
解:∵ ,∴
,∴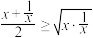 ,即
,即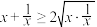 ,∴
,∴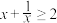 ,当且仅当
,当且仅当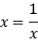 ,即
,即 时,
时, 有最小值,最小值为2.
有最小值,最小值为2.
请根据阅读材料解答下列问题
(1)已知如 ,求下列各式的值:
,求下列各式的值: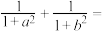
___________ .
(2)若正数 满足
满足 ,则
,则 的最小值为
的最小值为___________ .
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察;(2)整体设元;(3)整体代入;(4)整体求和等.
例如,
 ,求证:
,求证: .
.证明:原式
 .
.波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.
阅读材料二:基本不等式
 ,当且仅当
,当且仅当 时等号成立,它是解决最值问题的有力工具.
时等号成立,它是解决最值问题的有力工具.例如:在
 的条件下,当x为何值时,
的条件下,当x为何值时, 有最小值,最小值是多少?
有最小值,最小值是多少?解:∵
 ,∴
,∴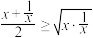 ,即
,即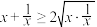 ,∴
,∴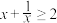 ,当且仅当
,当且仅当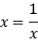 ,即
,即 时,
时, 有最小值,最小值为2.
有最小值,最小值为2.请根据阅读材料解答下列问题
(1)已知如
 ,求下列各式的值:
,求下列各式的值: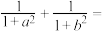
(2)若正数
 满足
满足 ,则
,则 的最小值为
的最小值为
您最近一年使用:0次
名校
解题方法
5 . 《见微知著》谈到:从一个简单的经典问题出发,从特殊到一般,由简单到复杂,从部分到整体,由低维到高维,知识与方法上的类比是探索发展的重要途径,是发现新问题、新结论的重要方法.
例如,已知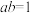 ,求证:
,求证: .
.
证明:原式 .
.
波利亚在《怎样解题》中也指出:“当你找到第一个蘑菇或作出第一个发现后,再四处看看,他们总是成群生长.”类似上述问题,我们有更多的式子满足以上特征.
请根据上述材料解答下列问题:
(1)已知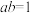 ,求
,求 的值;
的值;
(2)若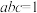 ,解方程
,解方程 ;
;
(3)若正数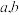 满足
满足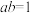 ,求
,求 的最小值.
的最小值.
例如,已知
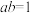 ,求证:
,求证: .
.证明:原式
 .
.波利亚在《怎样解题》中也指出:“当你找到第一个蘑菇或作出第一个发现后,再四处看看,他们总是成群生长.”类似上述问题,我们有更多的式子满足以上特征.
请根据上述材料解答下列问题:
(1)已知
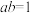 ,求
,求 的值;
的值;(2)若
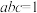 ,解方程
,解方程 ;
;(3)若正数
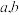 满足
满足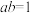 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次
2022-10-21更新
|
434次组卷
|
4卷引用:广东省中山市2022-2023学年高一上学期第一次调研数学试题
广东省中山市2022-2023学年高一上学期第一次调研数学试题四川省成都市第七中学2023年高三上学期1月月考数学文科试题四川省攀枝花市第三高级中学校2023-2024学年高一上学期10月月考数学试题(已下线)第03讲 第二章 一元二次函数、方程和不等式章节综合测试-【练透核心考点】
名校
6 . 《见微知著》谈到:从一个简单的经典问题出发,从特殊到一般,由简单到复杂:从部分到整体,由低维到高维,知识与方法上的类比是探索发展的重要途径,是思想阀门发现新问题、新结论的重要方法.阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察:(2)整体设元:(3)整体代入:(4)整体求和等.例如,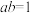 ,求证:
,求证: .证明:原式
.证明:原式 .波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.阅读材料二:基本不等式
.波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.阅读材料二:基本不等式 ,当且仅当
,当且仅当 时等号成立,它是解决最值问题的有力工具.例如:在
时等号成立,它是解决最值问题的有力工具.例如:在 的条件下,当x为何值时,
的条件下,当x为何值时, 有最小值,最小值是多少?
有最小值,最小值是多少?
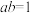 ,求证:
,求证: .证明:原式
.证明:原式 .波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.阅读材料二:基本不等式
.波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.阅读材料二:基本不等式 ,当且仅当
,当且仅当 时等号成立,它是解决最值问题的有力工具.例如:在
时等号成立,它是解决最值问题的有力工具.例如:在 的条件下,当x为何值时,
的条件下,当x为何值时, 有最小值,最小值是多少?
有最小值,最小值是多少?
您最近一年使用:0次
名校
解题方法
7 . 悬索桥(如图)的外观大漂亮,悬索的形状是平面几何中的悬链线. 年莱布尼兹和伯努利推导出某链线的方程为
年莱布尼兹和伯努利推导出某链线的方程为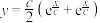 ,其中
,其中 为参数.当
为参数.当 时,该方程就是双曲余弦函数
时,该方程就是双曲余弦函数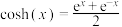 ,类似的我们有双曲正弦函数
,类似的我们有双曲正弦函数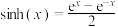 .
.

(1)从下列三个结论中选择一个进行证明,并求函数 的最小值;
的最小值;
①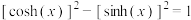 ;
;
②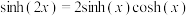 ;
;
③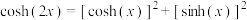 .
.
(2)求证: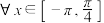 ,
,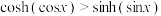 .
.
 年莱布尼兹和伯努利推导出某链线的方程为
年莱布尼兹和伯努利推导出某链线的方程为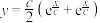 ,其中
,其中 为参数.当
为参数.当 时,该方程就是双曲余弦函数
时,该方程就是双曲余弦函数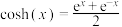 ,类似的我们有双曲正弦函数
,类似的我们有双曲正弦函数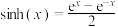 .
.
(1)从下列三个结论中选择一个进行证明,并求函数
 的最小值;
的最小值;①
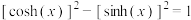 ;
;②
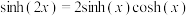 ;
;③
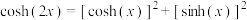 .
.(2)求证:
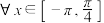 ,
,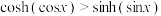 .
.
您最近一年使用:0次
2022-02-01更新
|
1267次组卷
|
7卷引用:江苏省苏州市2021-2022学年高一上学期期末数学试题
江苏省苏州市2021-2022学年高一上学期期末数学试题湖南省株洲市第二中学2021-2022学年高一下学期“同济大学”杯数理化联赛数学试题重庆市2023届高三下学期3月月度质量检测数学试题湖南省株洲市南方中学2022-2023学年高一下学期期末数学试题(已下线)重难点突破02 函数的综合应用(九大题型)(已下线)压轴题函数与导数新定义题(九省联考第19题模式)讲(已下线)压轴题三角函数新定义题(九省联考第19题模式)讲
名校
解题方法
8 . 《九章算术》是中国古代的一部数学专著,其中将由四个直角三角形组成的四面体称为“鳖臑”.在直四棱柱 中,E,F分别为线段
中,E,F分别为线段 与
与 上的中点.
上的中点.
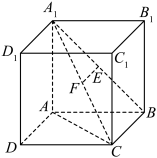
(1)求证: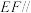 平面
平面 ;
;
(2)从三棱锥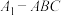 中选择合适的两条棱填空:__________⊥__________,使得三棱锥
中选择合适的两条棱填空:__________⊥__________,使得三棱锥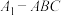 为“鳖臑”;并证明你的结论.
为“鳖臑”;并证明你的结论.
 中,E,F分别为线段
中,E,F分别为线段 与
与 上的中点.
上的中点.
(1)求证:
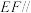 平面
平面 ;
;(2)从三棱锥
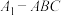 中选择合适的两条棱填空:__________⊥__________,使得三棱锥
中选择合适的两条棱填空:__________⊥__________,使得三棱锥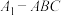 为“鳖臑”;并证明你的结论.
为“鳖臑”;并证明你的结论.
您最近一年使用:0次
2021-08-07更新
|
371次组卷
|
2卷引用:江苏省淮安市2020-2021学年高一下学期期末数学试题
解题方法
9 . 拉格朗日中值定理是微分学的基本定理之一,其内容为:如果函数 在闭区间
在闭区间 上的图象连续不断,在开区间
上的图象连续不断,在开区间 内的导数为
内的导数为 ,那么在区间
,那么在区间 内存在点
内存在点 ,使得
,使得 成立.设
成立.设 ,其中
,其中 为自然对数的底数,
为自然对数的底数, .易知,
.易知, 在实数集
在实数集 上有唯一零点
上有唯一零点 ,且
,且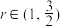 .
.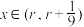 时,
时,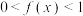 ;
;
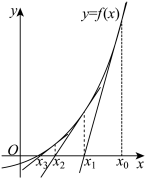
(2)从图形上看,函数 的零点就是函数
的零点就是函数 的图象与
的图象与 轴交点的横坐标.直接求解
轴交点的横坐标.直接求解 的零点
的零点 是困难的,运用牛顿法,我们可以得到
是困难的,运用牛顿法,我们可以得到 零点的近似解:先用二分法,可在
零点的近似解:先用二分法,可在 中选定一个
中选定一个 作为
作为 的初始近似值,使得
的初始近似值,使得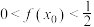 ,然后在点
,然后在点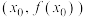 处作曲线
处作曲线 的切线,切线与
的切线,切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,称
,称 是
是 的一次近似值;在点
的一次近似值;在点 处作曲线
处作曲线 的切线,切线与
的切线,切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,称
,称 是
是 的二次近似值;重复以上过程,得
的二次近似值;重复以上过程,得 的近似值序列
的近似值序列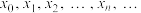 .
.
①当 时,证明:
时,证明: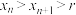 ;
;
②根据①的结论,运用数学归纳法可以证得: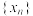 为递减数列,且
为递减数列,且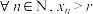 .请以此为前提条件,证明:
.请以此为前提条件,证明: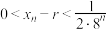 .
.
 在闭区间
在闭区间 上的图象连续不断,在开区间
上的图象连续不断,在开区间 内的导数为
内的导数为 ,那么在区间
,那么在区间 内存在点
内存在点 ,使得
,使得 成立.设
成立.设 ,其中
,其中 为自然对数的底数,
为自然对数的底数, .易知,
.易知, 在实数集
在实数集 上有唯一零点
上有唯一零点 ,且
,且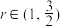 .
.
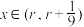 时,
时,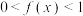 ;
;(2)从图形上看,函数
 的零点就是函数
的零点就是函数 的图象与
的图象与 轴交点的横坐标.直接求解
轴交点的横坐标.直接求解 的零点
的零点 是困难的,运用牛顿法,我们可以得到
是困难的,运用牛顿法,我们可以得到 零点的近似解:先用二分法,可在
零点的近似解:先用二分法,可在 中选定一个
中选定一个 作为
作为 的初始近似值,使得
的初始近似值,使得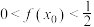 ,然后在点
,然后在点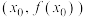 处作曲线
处作曲线 的切线,切线与
的切线,切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,称
,称 是
是 的一次近似值;在点
的一次近似值;在点 处作曲线
处作曲线 的切线,切线与
的切线,切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,称
,称 是
是 的二次近似值;重复以上过程,得
的二次近似值;重复以上过程,得 的近似值序列
的近似值序列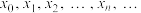 .
.①当
 时,证明:
时,证明: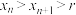 ;
;②根据①的结论,运用数学归纳法可以证得:
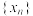 为递减数列,且
为递减数列,且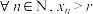 .请以此为前提条件,证明:
.请以此为前提条件,证明: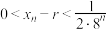 .
.
您最近一年使用:0次
名校
10 . 帕德近似是法国数学家亨利·帕德发明的用有理多项式近似特定函数的方法.给定两个正整数 ,
, ,函数
,函数 在
在 处的
处的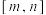 阶帕德近似定义为:
阶帕德近似定义为: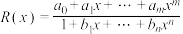 ,且满足:
,且满足: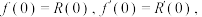
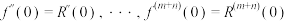 .(注:
.(注: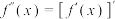 ,
,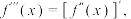
 为
为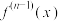 的导数)已知
的导数)已知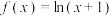 在
在 处的
处的 阶帕德近似为
阶帕德近似为 .
.
(1)求实数 的值;
的值;
(2)证明:当 时,
时, ;
;
(3)设 为实数,讨论方程
为实数,讨论方程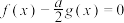 的解的个数.
的解的个数.
 ,
, ,函数
,函数 在
在 处的
处的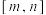 阶帕德近似定义为:
阶帕德近似定义为: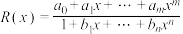 ,且满足:
,且满足: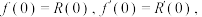
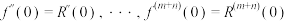 .(注:
.(注: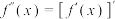 ,
,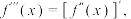
 为
为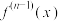 的导数)已知
的导数)已知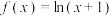 在
在 处的
处的 阶帕德近似为
阶帕德近似为 .
.(1)求实数
 的值;
的值;(2)证明:当
 时,
时, ;
;(3)设
 为实数,讨论方程
为实数,讨论方程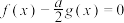 的解的个数.
的解的个数.
您最近一年使用:0次



