名校
1 . 已知函数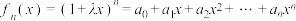 ,其中
,其中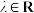 ,
, .
.
(1)若n=8,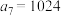 ,求
,求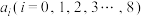 的最大值;
的最大值;
(2)若 ,求
,求 ;(用n表示)
;(用n表示)
(3)若 ,求证:
,求证: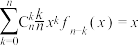 .
.
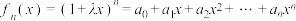 ,其中
,其中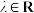 ,
, .
.(1)若n=8,
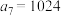 ,求
,求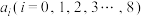 的最大值;
的最大值;(2)若
 ,求
,求 ;(用n表示)
;(用n表示)(3)若
 ,求证:
,求证: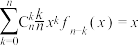 .
.
您最近一年使用:0次
名校
解题方法
2 . 已知F为抛物线C: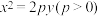 的焦点,点A在C上,
的焦点,点A在C上,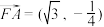 .点P(0,-2),M,N是抛物线上不同两点,直线PM和直线PN的斜率分别为
.点P(0,-2),M,N是抛物线上不同两点,直线PM和直线PN的斜率分别为 ,
, .
.
(1)求C的方程;
(2)存在点Q,当直线MN经过点Q时, 恒成立,请求出满足条件的所有点Q的坐标;
恒成立,请求出满足条件的所有点Q的坐标;
(3)对于(2)中的一个点Q,当直线MN经过点Q时,|MN|存在最小值,试求出这个最小值.
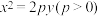 的焦点,点A在C上,
的焦点,点A在C上,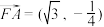 .点P(0,-2),M,N是抛物线上不同两点,直线PM和直线PN的斜率分别为
.点P(0,-2),M,N是抛物线上不同两点,直线PM和直线PN的斜率分别为 ,
, .
.(1)求C的方程;
(2)存在点Q,当直线MN经过点Q时,
 恒成立,请求出满足条件的所有点Q的坐标;
恒成立,请求出满足条件的所有点Q的坐标;(3)对于(2)中的一个点Q,当直线MN经过点Q时,|MN|存在最小值,试求出这个最小值.
您最近一年使用:0次
2024-05-20更新
|
897次组卷
|
2卷引用:江苏省苏锡常镇四市2024届高三教学情况调研(二)数学试题
名校
解题方法
3 . 有一个益智类的古堡探险闯关游戏,玩家每局都有甲、乙两座不同的古堡可供选择.已知某玩家古堡甲闯关成功的概率为 ,古堡乙闯关成功的概率为
,古堡乙闯关成功的概率为 .若该玩家第一局选择古堡甲闯关的概率为
.若该玩家第一局选择古堡甲闯关的概率为 ,前一局选择了古堡甲闯关,则继续选择古堡甲闯关的概率为
,前一局选择了古堡甲闯关,则继续选择古堡甲闯关的概率为 ;前一局选择了古堡乙闯关,则继续选择古堡乙闯关的概率为
;前一局选择了古堡乙闯关,则继续选择古堡乙闯关的概率为 .
.
(1)求该玩家第一局闯关成功的概率;
(2)记该玩家第 局选择古堡甲闯关的概率为
局选择古堡甲闯关的概率为 ,第
,第 局闯关成功的概率为
局闯关成功的概率为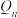 .
.
(i)求 和
和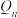 的表达式;
的表达式;
(ii)当 时,求证:
时,求证: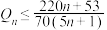 .
.
 ,古堡乙闯关成功的概率为
,古堡乙闯关成功的概率为 .若该玩家第一局选择古堡甲闯关的概率为
.若该玩家第一局选择古堡甲闯关的概率为 ,前一局选择了古堡甲闯关,则继续选择古堡甲闯关的概率为
,前一局选择了古堡甲闯关,则继续选择古堡甲闯关的概率为 ;前一局选择了古堡乙闯关,则继续选择古堡乙闯关的概率为
;前一局选择了古堡乙闯关,则继续选择古堡乙闯关的概率为 .
.(1)求该玩家第一局闯关成功的概率;
(2)记该玩家第
 局选择古堡甲闯关的概率为
局选择古堡甲闯关的概率为 ,第
,第 局闯关成功的概率为
局闯关成功的概率为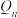 .
.(i)求
 和
和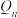 的表达式;
的表达式;(ii)当
 时,求证:
时,求证: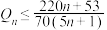 .
.
您最近一年使用:0次
解题方法
4 . “熵”常用来判断系统中信息含量的多少,也用来判断概率分布中随机变量的不确定性大小,一般熵越大表示随机变量的不确定性越明显.定义:随机变量 对应取值
对应取值 的概率为
的概率为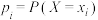 ,其单位为bit的熵为
,其单位为bit的熵为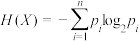 ,且
,且 .(当
.(当 ,规定
,规定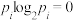 .)
.)
(1)若抛掷一枚硬币1次,正面向上的概率为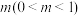 ,正面向上的次数为
,正面向上的次数为 ,分别比较
,分别比较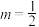 与
与 时对应
时对应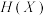 的大小,并根据你的理解说明结论的实际含义;
的大小,并根据你的理解说明结论的实际含义;
(2)若拋郑一枚质地均匀 的硬币 次,设
次,设 表示正面向上的总次数,
表示正面向上的总次数, 表示第
表示第 次反面向上的次数(0或1).
次反面向上的次数(0或1).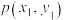 表示正面向上
表示正面向上 次且第
次且第 次反面向上
次反面向上 次的概率,如
次的概率,如 时,
时,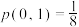 .对于两个离散的随机变量
.对于两个离散的随机变量 ,其单位为bit的联合熵记为
,其单位为bit的联合熵记为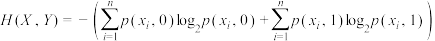 ,且
,且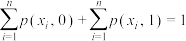 .
.
(ⅰ)当 时,求
时,求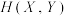 的值;
的值;
(ⅱ)求证: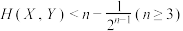 .
.
 对应取值
对应取值 的概率为
的概率为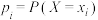 ,其单位为bit的熵为
,其单位为bit的熵为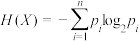 ,且
,且 .(当
.(当 ,规定
,规定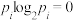 .)
.)(1)若抛掷一枚硬币1次,正面向上的概率为
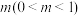 ,正面向上的次数为
,正面向上的次数为 ,分别比较
,分别比较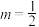 与
与 时对应
时对应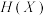 的大小,并根据你的理解说明结论的实际含义;
的大小,并根据你的理解说明结论的实际含义;(2)若拋郑一枚
 次,设
次,设 表示正面向上的总次数,
表示正面向上的总次数, 表示第
表示第 次反面向上的次数(0或1).
次反面向上的次数(0或1).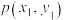 表示正面向上
表示正面向上 次且第
次且第 次反面向上
次反面向上 次的概率,如
次的概率,如 时,
时,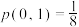 .对于两个离散的随机变量
.对于两个离散的随机变量 ,其单位为bit的联合熵记为
,其单位为bit的联合熵记为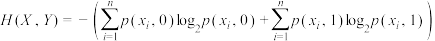 ,且
,且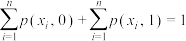 .
.(ⅰ)当
 时,求
时,求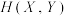 的值;
的值;(ⅱ)求证:
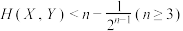 .
.
您最近一年使用:0次
解题方法
5 . 已知数列 的前n项和为
的前n项和为 .若对每一个
.若对每一个 ,有且仅有一个
,有且仅有一个 ,使得
,使得 ,则称
,则称 为“X数列”.记
为“X数列”.记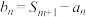 ,
, ,称数列
,称数列 为
为 的“余项数列”.
的“余项数列”.
(1)若 的前四项依次为0,1,
的前四项依次为0,1, ,1,试判断
,1,试判断 是否为“X数列”,并说明理由;
是否为“X数列”,并说明理由;
(2)若 ,证明
,证明 为“X数列”,并求它的“余项数列”的通项公式;
为“X数列”,并求它的“余项数列”的通项公式;
(3)已知正项数列 为“X数列”,且
为“X数列”,且 的“余项数列”为等差数列,证明:
的“余项数列”为等差数列,证明: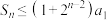 .
.
 的前n项和为
的前n项和为 .若对每一个
.若对每一个 ,有且仅有一个
,有且仅有一个 ,使得
,使得 ,则称
,则称 为“X数列”.记
为“X数列”.记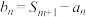 ,
, ,称数列
,称数列 为
为 的“余项数列”.
的“余项数列”.(1)若
 的前四项依次为0,1,
的前四项依次为0,1, ,1,试判断
,1,试判断 是否为“X数列”,并说明理由;
是否为“X数列”,并说明理由;(2)若
 ,证明
,证明 为“X数列”,并求它的“余项数列”的通项公式;
为“X数列”,并求它的“余项数列”的通项公式;(3)已知正项数列
 为“X数列”,且
为“X数列”,且 的“余项数列”为等差数列,证明:
的“余项数列”为等差数列,证明: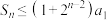 .
.
您最近一年使用:0次
名校
解题方法
6 . 已知椭圆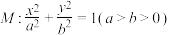 经过
经过 和
和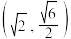 ,
,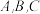 分别为椭圆的左顶点、右顶点、上顶点.
分别为椭圆的左顶点、右顶点、上顶点.
(1)求椭圆 的标准方程;
的标准方程;
(2)过 轴上点
轴上点 (点
(点 在椭圆
在椭圆 长轴上)作直线交椭圆
长轴上)作直线交椭圆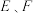 两点,且
两点,且 ,若
,若 ,求
,求 点的坐标;
点的坐标;
(3)过点 作直线交椭圆
作直线交椭圆 于
于 点,交直线
点,交直线 于
于 ,直线
,直线 于
于 轴相交于
轴相交于 ,求证:
,求证: 为定值,并求此定值.(其中
为定值,并求此定值.(其中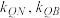 分别为直线
分别为直线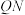 和直线l,
和直线l,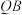 的斜率).
的斜率).
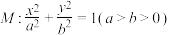 经过
经过 和
和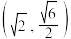 ,
,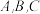 分别为椭圆的左顶点、右顶点、上顶点.
分别为椭圆的左顶点、右顶点、上顶点.(1)求椭圆
 的标准方程;
的标准方程;(2)过
 轴上点
轴上点 (点
(点 在椭圆
在椭圆 长轴上)作直线交椭圆
长轴上)作直线交椭圆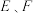 两点,且
两点,且 ,若
,若 ,求
,求 点的坐标;
点的坐标;(3)过点
 作直线交椭圆
作直线交椭圆 于
于 点,交直线
点,交直线 于
于 ,直线
,直线 于
于 轴相交于
轴相交于 ,求证:
,求证: 为定值,并求此定值.(其中
为定值,并求此定值.(其中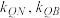 分别为直线
分别为直线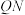 和直线l,
和直线l,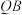 的斜率).
的斜率).
您最近一年使用:0次
名校
解题方法
7 . 已知双曲线E: 的左,右焦点分别为
的左,右焦点分别为 ,离心率为2,点B为
,离心率为2,点B为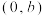 ,直线
,直线 与圆
与圆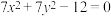 相切.
相切.
(1)求双曲线E方程;
(2)过 的直线l与双曲线E交于M,N两点,
的直线l与双曲线E交于M,N两点,
①若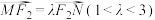 ,求
,求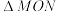 的面积取值范围:
的面积取值范围:
②若直线l的斜率为k,是否存在双曲线E上一点Q以及x轴上一点P,使四边形PMQN为菱形?若存在,求出 ;若不存在,请说明理由.
;若不存在,请说明理由.
 的左,右焦点分别为
的左,右焦点分别为 ,离心率为2,点B为
,离心率为2,点B为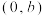 ,直线
,直线 与圆
与圆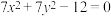 相切.
相切.(1)求双曲线E方程;
(2)过
 的直线l与双曲线E交于M,N两点,
的直线l与双曲线E交于M,N两点,①若
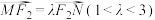 ,求
,求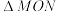 的面积取值范围:
的面积取值范围:②若直线l的斜率为k,是否存在双曲线E上一点Q以及x轴上一点P,使四边形PMQN为菱形?若存在,求出
 ;若不存在,请说明理由.
;若不存在,请说明理由.
您最近一年使用:0次
名校
8 . 设函数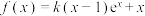 (
( ),其中
),其中 为自然对数的底数,
为自然对数的底数, 为实数.
为实数.
(1)若 在
在 上单调递增,求实数k的取值范围;
上单调递增,求实数k的取值范围;
(2)求 的零点的个数:;
的零点的个数:;
(3)若不等式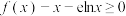 在
在 上恒成立,求k的取值范围.
上恒成立,求k的取值范围.
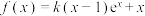 (
( ),其中
),其中 为自然对数的底数,
为自然对数的底数, 为实数.
为实数.(1)若
 在
在 上单调递增,求实数k的取值范围;
上单调递增,求实数k的取值范围;(2)求
 的零点的个数:;
的零点的个数:;(3)若不等式
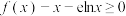 在
在 上恒成立,求k的取值范围.
上恒成立,求k的取值范围.
您最近一年使用:0次
2024·江西上饶·二模
9 . 对于数列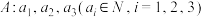 ,定义“
,定义“ 变换”:
变换”: 将数列
将数列 变换成数列
变换成数列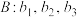 ,其中
,其中 ,且
,且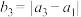 .这种“
.这种“ 变换”记作
变换”记作 ,继续对数列
,继续对数列 进行“
进行“ 变换”,得到数列
变换”,得到数列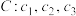 ,依此类推,当得到的数列各项均为0时变换结束.
,依此类推,当得到的数列各项均为0时变换结束.
(1)写出数列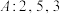 ,经过6次“
,经过6次“ 变换”后得到的数列;
变换”后得到的数列;
(2)若 不全相等,判断数列
不全相等,判断数列 经过不断的“
经过不断的“ 变换”是否会结束,并说明理由;
变换”是否会结束,并说明理由;
(3)设数列 经过
经过 次“
次“ 变换”得到的数列各项之和最小,求
变换”得到的数列各项之和最小,求 的最小值.
的最小值.
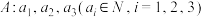 ,定义“
,定义“ 变换”:
变换”: 将数列
将数列 变换成数列
变换成数列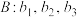 ,其中
,其中 ,且
,且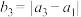 .这种“
.这种“ 变换”记作
变换”记作 ,继续对数列
,继续对数列 进行“
进行“ 变换”,得到数列
变换”,得到数列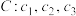 ,依此类推,当得到的数列各项均为0时变换结束.
,依此类推,当得到的数列各项均为0时变换结束.(1)写出数列
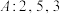 ,经过6次“
,经过6次“ 变换”后得到的数列;
变换”后得到的数列;(2)若
 不全相等,判断数列
不全相等,判断数列 经过不断的“
经过不断的“ 变换”是否会结束,并说明理由;
变换”是否会结束,并说明理由;(3)设数列
 经过
经过 次“
次“ 变换”得到的数列各项之和最小,求
变换”得到的数列各项之和最小,求 的最小值.
的最小值.
您最近一年使用:0次
解题方法
10 . 三角形的布洛卡点是法国数学家、数学教育学家克洛尔于1816年首次发现,但他的发现并未被当时的人们所注意.1875年,布洛卡点被一个数学爱好者布洛卡重新发现,并用他的名字命名.当 内一点
内一点 满足条件
满足条件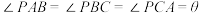 时,则称点
时,则称点 为
为 的布洛卡点,角
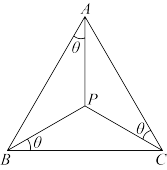
的布洛卡点,角 为布洛卡角.如图,在
为布洛卡角.如图,在 中,角
中,角 所对边长分别为
所对边长分别为 ,点
,点 为
为 的布洛卡点,其布洛卡角为
的布洛卡点,其布洛卡角为 .
.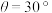 .求证:
.求证:
①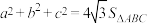 (
(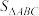 为
为 的面积);
的面积);
② 为等边三角形.
为等边三角形.
(2)若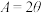 ,求证:
,求证: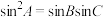 .
.
 内一点
内一点 满足条件
满足条件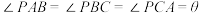 时,则称点
时,则称点 为
为 的布洛卡点,角
的布洛卡点,角 为布洛卡角.如图,在
为布洛卡角.如图,在 中,角
中,角 所对边长分别为
所对边长分别为 ,点
,点 为
为 的布洛卡点,其布洛卡角为
的布洛卡点,其布洛卡角为 .
.
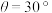 .求证:
.求证:①
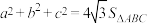 (
(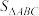 为
为 的面积);
的面积);②
 为等边三角形.
为等边三角形.(2)若
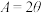 ,求证:
,求证: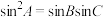 .
.
您最近一年使用:0次
2024-04-28更新
|
497次组卷
|
2卷引用:江苏省常州市教育学会2023-2024学年高一下学期4月学业水平监测数学试题



