解题方法
1 . 已知数列 ,其前
,其前 项和
项和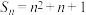 ,
,
(1)求数列 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列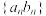 的前
的前 项和
项和 .
.
 ,其前
,其前 项和
项和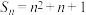 ,
,(1)求数列
 的通项公式;
的通项公式;(2)若
 ,求数列
,求数列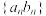 的前
的前 项和
项和 .
.
您最近一年使用:0次
解题方法
2 . (1)在复数范围内解方程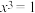 ;
;
(2)设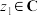 ,
,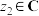 且
且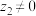 ,证明:
,证明: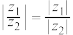 ;
;
(3)设复数数列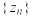 满足:
满足: ,且对任意正整数
,且对任意正整数 ,均有
,均有 .证明:对任意正偶数
.证明:对任意正偶数 ,均有
,均有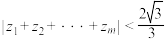 .
.
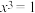 ;
;(2)设
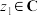 ,
,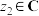 且
且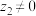 ,证明:
,证明: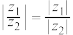 ;
;(3)设复数数列
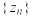 满足:
满足: ,且对任意正整数
,且对任意正整数 ,均有
,均有 .证明:对任意正偶数
.证明:对任意正偶数 ,均有
,均有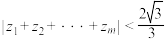 .
.
您最近一年使用:0次
3 . 母函数(又称生成函数)就是一列用来展示一串数字的挂衣架.这是数学家赫伯特·维尔夫对母函数的一个形象且精妙的比喻.对于任意数列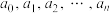 ,即用如下方法与一个函数联系起来:
,即用如下方法与一个函数联系起来: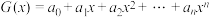 ,则称
,则称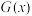 是数列
是数列 的生成函数.例如:求方程
的生成函数.例如:求方程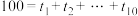 的非负整数解的个数.设此方程的生成函数为
的非负整数解的个数.设此方程的生成函数为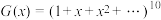 ,其中x的指数代表
,其中x的指数代表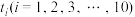 的值.
的值.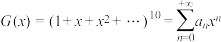 ,则非负整数解的个数为
,则非负整数解的个数为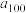 .若
.若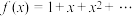 ,则
,则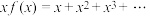 ,可得
,可得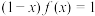 ,于是可得函数
,于是可得函数 的收缩表达式为:
的收缩表达式为: .故
.故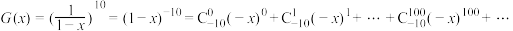 (广义的二项式定理:两个数之和的任意实数次幂可以展开为类似项之和的恒等式)则
(广义的二项式定理:两个数之和的任意实数次幂可以展开为类似项之和的恒等式)则 根据以上材料,解决下述问题:定义“规范01数列”
根据以上材料,解决下述问题:定义“规范01数列” 如下:
如下: 共有
共有 项,其中m项为0,m项为1,且对任意
项,其中m项为0,m项为1,且对任意 ,
,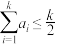 ,不同的“规范01数列”个数记为
,不同的“规范01数列”个数记为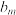 .
.
(1)判断以下数列是否为“规范01数列”;
①0,1,0,1,0,1;②0,0,1,1,1,0,0,1;③0,1,0,0,0,1,1,1.
(2)规定 ,计算
,计算 ,
, ,
, ,
,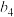 的值,归纳数列
的值,归纳数列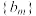 的递推公式;
的递推公式;
(3)设数列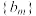 对应的生成函数为
对应的生成函数为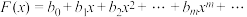
①结合 与
与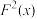 之间的关系,推导
之间的关系,推导 的收缩表达式;
的收缩表达式;
②求数列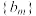 的通项公式.
的通项公式.
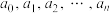 ,即用如下方法与一个函数联系起来:
,即用如下方法与一个函数联系起来: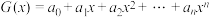 ,则称
,则称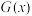 是数列
是数列 的生成函数.例如:求方程
的生成函数.例如:求方程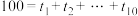 的非负整数解的个数.设此方程的生成函数为
的非负整数解的个数.设此方程的生成函数为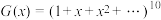 ,其中x的指数代表
,其中x的指数代表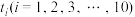 的值.
的值.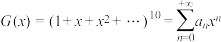 ,则非负整数解的个数为
,则非负整数解的个数为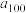 .若
.若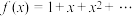 ,则
,则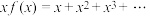 ,可得
,可得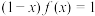 ,于是可得函数
,于是可得函数 的收缩表达式为:
的收缩表达式为: .故
.故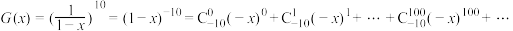 (广义的二项式定理:两个数之和的任意实数次幂可以展开为类似项之和的恒等式)则
(广义的二项式定理:两个数之和的任意实数次幂可以展开为类似项之和的恒等式)则 根据以上材料,解决下述问题:定义“规范01数列”
根据以上材料,解决下述问题:定义“规范01数列” 如下:
如下: 共有
共有 项,其中m项为0,m项为1,且对任意
项,其中m项为0,m项为1,且对任意 ,
,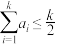 ,不同的“规范01数列”个数记为
,不同的“规范01数列”个数记为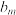 .
.(1)判断以下数列是否为“规范01数列”;
①0,1,0,1,0,1;②0,0,1,1,1,0,0,1;③0,1,0,0,0,1,1,1.
(2)规定
 ,计算
,计算 ,
, ,
, ,
,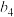 的值,归纳数列
的值,归纳数列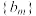 的递推公式;
的递推公式;(3)设数列
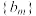 对应的生成函数为
对应的生成函数为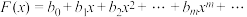
①结合
 与
与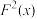 之间的关系,推导
之间的关系,推导 的收缩表达式;
的收缩表达式;②求数列
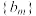 的通项公式.
的通项公式.
您最近一年使用:0次
解题方法
4 . 已知数列 的前
的前 项和为
项和为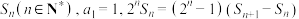 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列 的前
的前 项和
项和 .
.
 的前
的前 项和为
项和为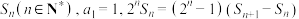 .
.(1)求数列
 的通项公式;
的通项公式;(2)若
 ,求数列
,求数列 的前
的前 项和
项和 .
.
您最近一年使用:0次
2024-09-05更新
|
1624次组卷
|
4卷引用:河北省保定部分高中2023届高三第三次模拟数学试题
河北省保定部分高中2023届高三第三次模拟数学试题(已下线)周测13数列通项公式、求和(一轮好卷提升卷)(已下线)滚动月考卷2 (高三大一轮好卷提升卷)山东省青岛市即墨实验高级中学2025届高三上学期第一次月考数学试题
5 . 对于任意正整数n,进行如下操作:若n为偶数,则对n不断地除以2,直到得到一个奇数,记这个奇数为 ;若n为奇数,则对
;若n为奇数,则对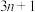 不断地除以2,直到得出一个奇数,记这个奇数为
不断地除以2,直到得出一个奇数,记这个奇数为 .若
.若 ,则称正整数n为“理想数”.
,则称正整数n为“理想数”.
(1)求20以内的质数“理想数”;
(2)已知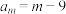 .求m的值;
.求m的值;
(3)将所有“理想数”从小至大依次排列,逐一取倒数后得到数列 ,记
,记 的前n项和为
的前n项和为 ,证明:
,证明: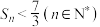 .
.
 ;若n为奇数,则对
;若n为奇数,则对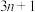 不断地除以2,直到得出一个奇数,记这个奇数为
不断地除以2,直到得出一个奇数,记这个奇数为 .若
.若 ,则称正整数n为“理想数”.
,则称正整数n为“理想数”.(1)求20以内的质数“理想数”;
(2)已知
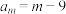 .求m的值;
.求m的值;(3)将所有“理想数”从小至大依次排列,逐一取倒数后得到数列
 ,记
,记 的前n项和为
的前n项和为 ,证明:
,证明: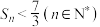 .
.
您最近一年使用:0次
2024-08-10更新
|
1107次组卷
|
8卷引用:河北省秦皇岛市山海关第一中学2025届高三上学期一模数学试题
6 . 如果项数均为n的数列 满足
满足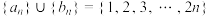 ,且
,且 为奇数时,
为奇数时,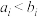 ;
; 为偶数时,
为偶数时,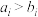 ,其中
,其中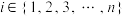 ,那么就称
,那么就称 为“互补交叉数列”,记
为“互补交叉数列”,记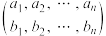 为
为 的“互补交叉数列对”,
的“互补交叉数列对”, 为
为 的前
的前 项和.
项和.
(1)若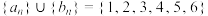 ,且
,且 ,写出所有满足条件的“互补交叉数列对";
,写出所有满足条件的“互补交叉数列对";
(2)当 为“互补交叉数列”时,
为“互补交叉数列”时,
(i)证明: 取最大值时,存在
取最大值时,存在 ;
;
(ii)当 为偶数时,求
为偶数时,求 的最大值.
的最大值.
 满足
满足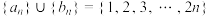 ,且
,且 为奇数时,
为奇数时,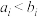 ;
; 为偶数时,
为偶数时,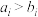 ,其中
,其中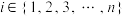 ,那么就称
,那么就称 为“互补交叉数列”,记
为“互补交叉数列”,记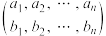 为
为 的“互补交叉数列对”,
的“互补交叉数列对”, 为
为 的前
的前 项和.
项和.(1)若
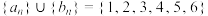 ,且
,且 ,写出所有满足条件的“互补交叉数列对";
,写出所有满足条件的“互补交叉数列对";(2)当
 为“互补交叉数列”时,
为“互补交叉数列”时,(i)证明:
 取最大值时,存在
取最大值时,存在 ;
;(ii)当
 为偶数时,求
为偶数时,求 的最大值.
的最大值.
您最近一年使用:0次
2024·河北·模拟预测
解题方法
7 . 一个不透明的袋子中装有大小、质地相同的40个小球,其中10个红球,10个黄球,20个绿球,依次随机抽取小球,每次只取1个小球,完成下列问题:
(1)若取出的小球不再放回,
①求最后取完的小球是黄球的概率;
②求红球比其余两种颜色小球更早取完的概率;
③设随机变量 为最后一个红球被取出时所需的取球次数,求
为最后一个红球被取出时所需的取球次数,求 ;
;
(2)若取出的小球又放回袋中,直到取到红球就停止取球,且最多取 次球,设随机变量
次球,设随机变量 为取球次数,证明:
为取球次数,证明: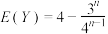 .
.
(1)若取出的小球不再放回,
①求最后取完的小球是黄球的概率;
②求红球比其余两种颜色小球更早取完的概率;
③设随机变量
 为最后一个红球被取出时所需的取球次数,求
为最后一个红球被取出时所需的取球次数,求 ;
;(2)若取出的小球又放回袋中,直到取到红球就停止取球,且最多取
 次球,设随机变量
次球,设随机变量 为取球次数,证明:
为取球次数,证明: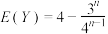 .
.
您最近一年使用:0次
8 . “完全数”是一类特殊的自然数,它的所有正因数的和等于它自身的两倍.寻找“完全数”需要用到函数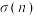 ,记函数
,记函数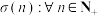 ,
,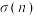 为
为 的所有正因数之和.
的所有正因数之和.
(1)判断28是否为完全数,并说明理由.
(2)已知 ,若
,若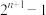 为质数,证明:
为质数,证明: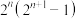 为完全数.
为完全数.
(3)已知 ,求
,求 ,
,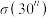 的值.
的值.
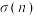 ,记函数
,记函数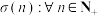 ,
,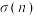 为
为 的所有正因数之和.
的所有正因数之和.(1)判断28是否为完全数,并说明理由.
(2)已知
 ,若
,若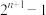 为质数,证明:
为质数,证明: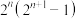 为完全数.
为完全数.(3)已知
 ,求
,求 ,
,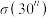 的值.
的值.
您最近一年使用:0次
2024-06-18更新
|
578次组卷
|
3卷引用:河北省秦皇岛市青龙满族自治县第一中学2024届高三下学期5月模拟考试数学试题
名校
解题方法
9 . 已知数列 的前
的前 项和为
项和为 ,且
,且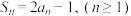 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求证: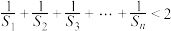 .
.
 的前
的前 项和为
项和为 ,且
,且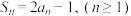 .
.(1)求数列
 的通项公式;
的通项公式;(2)求证:
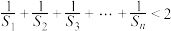 .
.
您最近一年使用:0次
2024-06-17更新
|
861次组卷
|
4卷引用:2024届河北省邢台市部分高中二模数学试题
2024届河北省邢台市部分高中二模数学试题河北省衡水中学2023-2024学年高三下学期期中自我提升测试数学试题(已下线)重难点突破01 数列的综合应用(十三大题型)-1(已下线)周测13数列通项公式、求和(一轮好卷提升卷)
名校
10 . 2021年教育部印发的《进一步加强中小学生体质健康管理工作的通知》中提出,中小学校要保障学生每天校内、校外各1小时体育活动时间,每天统一安排30分钟的大课间体育活动.一学校某体育项目测试有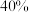 的人满分,而该校有
的人满分,而该校有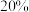 的学生每天运动时间超过两个小时,这些人体育项目测试满分率为
的学生每天运动时间超过两个小时,这些人体育项目测试满分率为 .
.
(1)从该校随机抽取三人,三人中体育项目测试相互独立,求三人中满分人数的分布列和期望;
(2)现从每天运动时间不超过两个小时的学生中任意调查一名学生,求他体育项目测试满分的概率;
(3)体育测试前甲、乙、丙三人传球做热身训练,每次传球,传球者等可能地将球传给另外两个人中的任何一人,第1次由甲将球传出,求第n次传球后球在乙手中的概率.
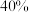 的人满分,而该校有
的人满分,而该校有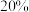 的学生每天运动时间超过两个小时,这些人体育项目测试满分率为
的学生每天运动时间超过两个小时,这些人体育项目测试满分率为 .
.(1)从该校随机抽取三人,三人中体育项目测试相互独立,求三人中满分人数的分布列和期望;
(2)现从每天运动时间不超过两个小时的学生中任意调查一名学生,求他体育项目测试满分的概率;
(3)体育测试前甲、乙、丙三人传球做热身训练,每次传球,传球者等可能地将球传给另外两个人中的任何一人,第1次由甲将球传出,求第n次传球后球在乙手中的概率.
您最近一年使用:0次
2024-06-14更新
|
446次组卷
|
2卷引用:河北省邯郸市部分示范性高中2024届高三下学期三模数学试题



