1 . 2024巴黎奥运会已圆满结束,中国体育健儿披荆斩棘,顽强拼搏,取得了骄人的成绩.下列有关巴黎奥运会的团体中不能构成集合的是( )
| A.全体参赛国家 | B.全体裁判员 |
| C.全体荣获金牌的运动员 | D.全体表现较好的运动员 |
您最近一年使用:0次
2 . 设A是由若干个正整数组成的集合,且存在3个不同的元素a,b,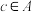 ,使得
,使得 ,则称A为“等差集”.
,则称A为“等差集”.
(1)若集合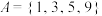 ,
,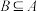 ,且B是“等差集”,用列举法表示所有满足条件的B;
,且B是“等差集”,用列举法表示所有满足条件的B;
(2)若集合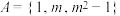 是“等差集”,求m的值;
是“等差集”,求m的值;
(3)已知正整数 ,证明:
,证明: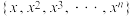 不是“等差集”.
不是“等差集”.
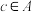 ,使得
,使得 ,则称A为“等差集”.
,则称A为“等差集”.(1)若集合
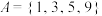 ,
,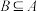 ,且B是“等差集”,用列举法表示所有满足条件的B;
,且B是“等差集”,用列举法表示所有满足条件的B;(2)若集合
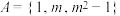 是“等差集”,求m的值;
是“等差集”,求m的值;(3)已知正整数
 ,证明:
,证明: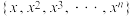 不是“等差集”.
不是“等差集”.
您最近一年使用:0次
2024-10-22更新
|
426次组卷
|
13卷引用:安徽省名校联盟2024-2025学年高一上学期10月大联考数学试卷
安徽省名校联盟2024-2025学年高一上学期10月大联考数学试卷江西省多校2024-2025学年高一上学期10月月考数学试题河南省名校联考2024-2025学年高一上学期第一次月考数学试题陕西省西安市黄河中学2024-2025学年高一上学期第一次月考数学试题内蒙古名校联盟2024-2025学年高一上学期10月大联考数学试题辽宁省凌源市2024-2025学年高一上学期第一次月考(10月)数学卷辽宁省朝阳市建平县实验中学2024-2025学年高一上学期10月月考数学试题河北省保定市安国中学2024-2025学年高一上学期第一次月考数学试题湖南省郴州市部分学校2024-2025学年高二上学期第一次月考数学试题湖南省多校联考2024-2025学年高二上学期10月月考数学试题陕西省咸阳市乾县杨汉中学2024-2025学年高二上学期第一次阶段性测试数学试卷广西钦州市第四中学2025届高三上学期8月考试数学试题甘肃省陇南市礼县第二中学2024-2025学年高二上学期第一次阶段性检测数学试卷
名校
3 . 下列各组对象能构成集合的有( )
| A.南昌大学2024级大一新生 | B.我国第一位获得奥运会金牌的运动员 |
| C.体型庞大的海洋生物 | D.唐宋八大家 |
您最近一年使用:0次
2024-10-22更新
|
333次组卷
|
6卷引用:安徽省名校联盟2024-2025学年高一上学期10月大联考数学试卷
名校
4 . 下列命题中,正确的是( )
A.集合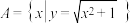 , , 表示同一集合 表示同一集合 |
B.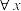 , ,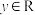 ,都有 ,都有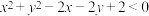 为真命题 为真命题 |
C.集合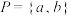 ,集合 ,集合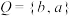 ,则 ,则 |
D.设 ,则“ ,则“ ”是“ ”是“ ”的充要条件 ”的充要条件 |
您最近一年使用:0次
2024-10-22更新
|
226次组卷
|
3卷引用:安徽省阜阳市第三中学2024-2025学年高一上学期10月月考数学试题
解题方法
5 . 某体育局为调查学生观看第33届巴黎奥运会的情况,统计了某高中高一(1)班55名学生的观看情况:55名学生观看比赛项目都集中在球类比赛、水上运动比赛、田径比赛这三类,其中8名学生只观看了球类比赛,5名学生只观看了水上运动比赛,6名学生只观看了田径比赛,既观看过球类比赛又观看过水上运动比赛的学生有24名,既观看过球类比赛又观看过田径比赛的学生有20名,既观看过水上运动比赛又观看过田径比赛的学生有18名,则该班这三类比赛都观看过的学生人数为( )
| A.10 | B.11 | C.12 | D.13 |
您最近一年使用:0次
2024-10-18更新
|
0次组卷
|
2卷引用:安徽省安庆市怀宁县高河中学2024-2025学年高一上学期10月月考数学试题
名校
解题方法
6 . 学校统计某班45名学生参加音乐、科学、体育3个兴趣小组的情况,其中有20名学生参加了音乐小组,有21名学生参加了科学小组,有22名学生参加了体育小组,有24名学生只参加了1个兴趣小组,有12名学生只参加了2个兴趣小组,则3个兴趣小组都没参加的学生有( )
| A.5名 | B.4名 | C.3名 | D.2名 |
您最近一年使用:0次
2024-10-16更新
|
291次组卷
|
6卷引用:安徽省名校联盟2024-2025学年高一上学期10月大联考数学试卷
7 . 对于正整数集合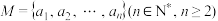 ,如果对于M中的任意两个元素x,y,都有
,如果对于M中的任意两个元素x,y,都有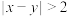 ,则称M为“好集合”.
,则称M为“好集合”.
(1)试判断集合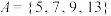 和
和 是否为“好集合”?并说明理由;
是否为“好集合”?并说明理由;
(2)若集合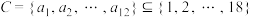 ,证明:C不可能是“好集合”;
,证明:C不可能是“好集合”;
(3)若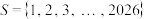 ,D是S的子集,且D是“好集合”,求D所含元素个数的最大值.
,D是S的子集,且D是“好集合”,求D所含元素个数的最大值.
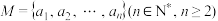 ,如果对于M中的任意两个元素x,y,都有
,如果对于M中的任意两个元素x,y,都有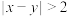 ,则称M为“好集合”.
,则称M为“好集合”.(1)试判断集合
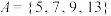 和
和 是否为“好集合”?并说明理由;
是否为“好集合”?并说明理由;(2)若集合
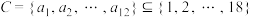 ,证明:C不可能是“好集合”;
,证明:C不可能是“好集合”;(3)若
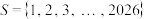 ,D是S的子集,且D是“好集合”,求D所含元素个数的最大值.
,D是S的子集,且D是“好集合”,求D所含元素个数的最大值.
您最近一年使用:0次
8 . 设集合 是
是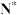 的非空子集,若对任意
的非空子集,若对任意 ,
,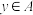 ,都有
,都有 ,则称集合
,则称集合 具有性质
具有性质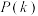 .
.
(1)试判断集合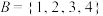 和
和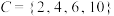 是否具有性质
是否具有性质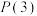 ,并说明理由;
,并说明理由;
(2)已知集合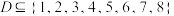 ,若
,若 具有性质
具有性质 且恰有4个元素,直接写出符合条件的集合
且恰有4个元素,直接写出符合条件的集合 ;(写出3个即可)
;(写出3个即可)
(3)已知集合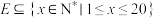 ,若
,若 具有性质
具有性质 ,证明:
,证明: 中的元素个数不大于10.
中的元素个数不大于10.
 是
是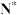 的非空子集,若对任意
的非空子集,若对任意 ,
,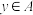 ,都有
,都有 ,则称集合
,则称集合 具有性质
具有性质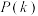 .
.(1)试判断集合
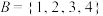 和
和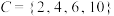 是否具有性质
是否具有性质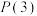 ,并说明理由;
,并说明理由;(2)已知集合
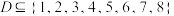 ,若
,若 具有性质
具有性质 且恰有4个元素,直接写出符合条件的集合
且恰有4个元素,直接写出符合条件的集合 ;(写出3个即可)
;(写出3个即可)(3)已知集合
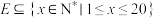 ,若
,若 具有性质
具有性质 ,证明:
,证明: 中的元素个数不大于10.
中的元素个数不大于10.
您最近一年使用:0次
名校
9 . 已知集合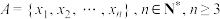 ,若对任意
,若对任意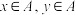 ,都有
,都有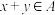 或
或 ,则称集合
,则称集合 具有“包容”性.
具有“包容”性.
(1)判断集合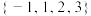 和集合
和集合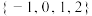 是否具有“包容”性;
是否具有“包容”性;
(2)若集合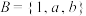 具有“包容”性,求
具有“包容”性,求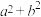 的值;
的值;
(3)若集合 具有“包容”性,且集合
具有“包容”性,且集合 中的元素共有6个,
中的元素共有6个,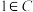 ,试确定集合
,试确定集合 .
.
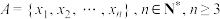 ,若对任意
,若对任意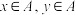 ,都有
,都有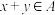 或
或 ,则称集合
,则称集合 具有“包容”性.
具有“包容”性.(1)判断集合
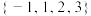 和集合
和集合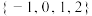 是否具有“包容”性;
是否具有“包容”性;(2)若集合
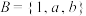 具有“包容”性,求
具有“包容”性,求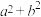 的值;
的值;(3)若集合
 具有“包容”性,且集合
具有“包容”性,且集合 中的元素共有6个,
中的元素共有6个,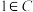 ,试确定集合
,试确定集合 .
.
您最近一年使用:0次
2024-09-27更新
|
476次组卷
|
6卷引用:安徽省亳州市涡阳县2024-2025学年高一上学期10月月考数学试题
名校
10 . 定义1:对于一个数集 ,定义一种运算
,定义一种运算 ,对任意
,对任意 都有
都有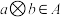 ,则称集合
,则称集合 关于运算
关于运算 是封闭的(例如:自然数集
是封闭的(例如:自然数集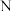 对于加法运算是封闭的).
对于加法运算是封闭的).
定义2:对于一个数集 ,若存在一个元素
,若存在一个元素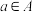 ,使得任意
,使得任意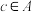 ,满足
,满足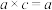 ,则称
,则称 为集合
为集合 中的零元,若存在一个元素
中的零元,若存在一个元素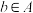 ,使得任意
,使得任意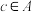 ,满足
,满足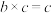 ,则称
,则称 为集合
为集合 中的单位元(例如:0和1分别为自然数集
中的单位元(例如:0和1分别为自然数集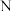 中的零元和单位元).
中的零元和单位元).
定义3:对于一个数集 ,如果满足下列关系:
,如果满足下列关系:
①有零元和单位元;
②关于加、减、乘、除(除数不为0)四种运算都是封闭的;
③对于乘法和加法都满足交换律和结合律,且满足乘法对加法的分配律,则称这个数集 是一个数域.
是一个数域.
(1)指出常用数集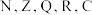 中,那些数集可以构成数域(不需要证明);
中,那些数集可以构成数域(不需要证明);
(2)已知集合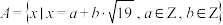 ,证明:集合
,证明:集合 关于乘法运算是封闭的;
关于乘法运算是封闭的;
(3)已知集合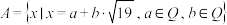 ,证明:集合
,证明:集合 是一个数域.
是一个数域.
 ,定义一种运算
,定义一种运算 ,对任意
,对任意 都有
都有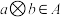 ,则称集合
,则称集合 关于运算
关于运算 是封闭的(例如:自然数集
是封闭的(例如:自然数集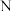 对于加法运算是封闭的).
对于加法运算是封闭的).定义2:对于一个数集
 ,若存在一个元素
,若存在一个元素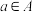 ,使得任意
,使得任意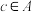 ,满足
,满足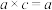 ,则称
,则称 为集合
为集合 中的零元,若存在一个元素
中的零元,若存在一个元素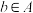 ,使得任意
,使得任意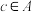 ,满足
,满足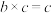 ,则称
,则称 为集合
为集合 中的单位元(例如:0和1分别为自然数集
中的单位元(例如:0和1分别为自然数集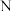 中的零元和单位元).
中的零元和单位元).定义3:对于一个数集
 ,如果满足下列关系:
,如果满足下列关系:①有零元和单位元;
②关于加、减、乘、除(除数不为0)四种运算都是封闭的;
③对于乘法和加法都满足交换律和结合律,且满足乘法对加法的分配律,则称这个数集
 是一个数域.
是一个数域. (1)指出常用数集
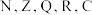 中,那些数集可以构成数域(不需要证明);
中,那些数集可以构成数域(不需要证明);(2)已知集合
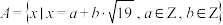 ,证明:集合
,证明:集合 关于乘法运算是封闭的;
关于乘法运算是封闭的;(3)已知集合
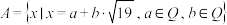 ,证明:集合
,证明:集合 是一个数域.
是一个数域.
您最近一年使用:0次
2024-05-22更新
|
991次组卷
|
7卷引用:安徽省宿州市省、市示范高中2023-2024学年高一下学期4月期中考试数学试题
安徽省宿州市省、市示范高中2023-2024学年高一下学期4月期中考试数学试题(已下线)第1章 集合综合测试-【暑假自学课】(苏教版2019必修第一册)(已下线)初升高开学考数学模拟卷02-2024年初升高数学无忧衔接(通用版)(已下线)【讲-提升版】1.1集合(高三一轮)(已下线)【讲-提升版】1.1集合(高三一轮)1(已下线)专题1 以集合为主体的新定义压轴大题(过关集训)(已下线)专题7 线性代数、抽象代数与数论背景的新定义压轴大题(三)【讲】



