1 . 已知集合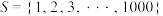 ,设
,设 是
是 的至少含有两个元素的子集,对于
的至少含有两个元素的子集,对于 中的任意两个不同的元素
中的任意两个不同的元素 ,若
,若 都不能整除
都不能整除 ,则称集合
,则称集合 是
是 的“好子集”.
的“好子集”.
①集合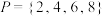 与
与 是集合
是集合 的“好子集”的是
的“好子集”的是______ ;
②集合 的“好子集”
的“好子集” 所含元素个数的最大值为
所含元素个数的最大值为______ .
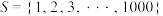 ,设
,设 是
是 的至少含有两个元素的子集,对于
的至少含有两个元素的子集,对于 中的任意两个不同的元素
中的任意两个不同的元素 ,若
,若 都不能整除
都不能整除 ,则称集合
,则称集合 是
是 的“好子集”.
的“好子集”.①集合
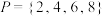 与
与 是集合
是集合 的“好子集”的是
的“好子集”的是②集合
 的“好子集”
的“好子集” 所含元素个数的最大值为
所含元素个数的最大值为
您最近一年使用:0次
名校
解题方法
2 . 设集合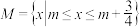 ,
,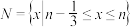 ,且M,N都是集合
,且M,N都是集合 的子集,如果把
的子集,如果把 叫做集合
叫做集合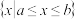 的“长度”,那么集合
的“长度”,那么集合 的“长度”的最小值是( )
的“长度”的最小值是( )
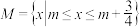 ,
,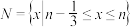 ,且M,N都是集合
,且M,N都是集合 的子集,如果把
的子集,如果把 叫做集合
叫做集合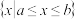 的“长度”,那么集合
的“长度”,那么集合 的“长度”的最小值是( )
的“长度”的最小值是( )A. | B. | C. | D. |
您最近一年使用:0次
名校
解题方法
3 . 设集合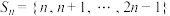 ,若X是
,若X是 的子集,把X中所有数的和称为X的“容量”(规定空集的容量为0),若X的容量为奇(偶)数,则称X为
的子集,把X中所有数的和称为X的“容量”(规定空集的容量为0),若X的容量为奇(偶)数,则称X为 的奇(偶)子集.
的奇(偶)子集.
(1)当 时,写出
时,写出 的所有奇子集;
的所有奇子集;
(2)求证:当 时,
时, 的所有奇子集的个数等于偶子集的个数;
的所有奇子集的个数等于偶子集的个数;
(3)当 时,求
时,求 的所有奇子集的容量之和.
的所有奇子集的容量之和.
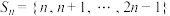 ,若X是
,若X是 的子集,把X中所有数的和称为X的“容量”(规定空集的容量为0),若X的容量为奇(偶)数,则称X为
的子集,把X中所有数的和称为X的“容量”(规定空集的容量为0),若X的容量为奇(偶)数,则称X为 的奇(偶)子集.
的奇(偶)子集.(1)当
 时,写出
时,写出 的所有奇子集;
的所有奇子集;(2)求证:当
 时,
时, 的所有奇子集的个数等于偶子集的个数;
的所有奇子集的个数等于偶子集的个数;(3)当
 时,求
时,求 的所有奇子集的容量之和.
的所有奇子集的容量之和.
您最近一年使用:0次
2024-08-29更新
|
372次组卷
|
2卷引用:北京市八一学校2024-2025学年高一上学期10月月考数学试题
4 . 在由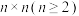 个实数组成的
个实数组成的 行
行 列的数表中,
列的数表中, 表示第
表示第 行第
行第 列的数(如图是一个3行3列的数表,
列的数(如图是一个3行3列的数表,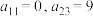 ),记
),记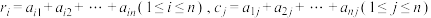 .若满足
.若满足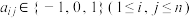 ,且
,且 两两不等,则称此表为“
两两不等,则称此表为“ 阶
阶 表”.记
表”.记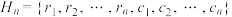 .
.
(1)请写出一个“2阶 表”;
表”;
(2)对任意一个“ 阶
阶 表”,若整数
表”,若整数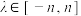 ,且
,且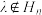 ,求证:
,求证: 为偶数;
为偶数;
(3)求证:不存在“5阶 表”.
表”.
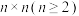 个实数组成的
个实数组成的 行
行 列的数表中,
列的数表中, 表示第
表示第 行第
行第 列的数(如图是一个3行3列的数表,
列的数(如图是一个3行3列的数表,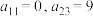 ),记
),记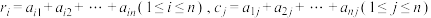 .若满足
.若满足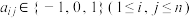 ,且
,且 两两不等,则称此表为“
两两不等,则称此表为“ 阶
阶 表”.记
表”.记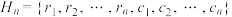 .
.| 0 | 3 | 2 |
| 1 | 2 | 9 |
| 3 | 4 | 1 |
 表”;
表”;(2)对任意一个“
 阶
阶 表”,若整数
表”,若整数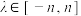 ,且
,且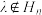 ,求证:
,求证: 为偶数;
为偶数;(3)求证:不存在“5阶
 表”.
表”.
您最近一年使用:0次
名校
5 . 已知 为实数集的一个非空子集,称
为实数集的一个非空子集,称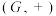 是一个加法群,如果
是一个加法群,如果 连同其上的加法运算满足如下四条性质:
连同其上的加法运算满足如下四条性质:
①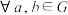 ,
, ;
;
② ,
, ;
;
③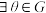 ,
,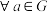 ,使得
,使得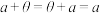 ;
;
④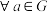 ,
, ,使得
,使得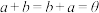 .
.
例如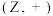 是一个无限元加法群,
是一个无限元加法群, 是一个单元素加法群.
是一个单元素加法群.
(1)令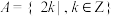 ,
,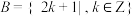 ,分别判断
,分别判断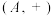 ,
,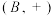 是否为加法群,并说明理由;
是否为加法群,并说明理由;
(2)已知非空集合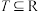 ,并且
,并且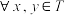 ,有
,有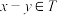 ,求证:
,求证: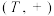 是一个加法群;
是一个加法群;
(3)已知非空集合 ,并且
,并且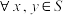 ,有
,有 ,求证:存在
,求证:存在 ,使得
,使得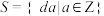 .
.
 为实数集的一个非空子集,称
为实数集的一个非空子集,称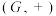 是一个加法群,如果
是一个加法群,如果 连同其上的加法运算满足如下四条性质:
连同其上的加法运算满足如下四条性质:①
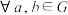 ,
, ;
;②
 ,
, ;
;③
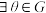 ,
,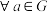 ,使得
,使得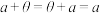 ;
;④
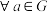 ,
, ,使得
,使得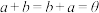 .
.例如
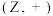 是一个无限元加法群,
是一个无限元加法群, 是一个单元素加法群.
是一个单元素加法群.(1)令
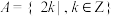 ,
,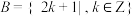 ,分别判断
,分别判断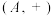 ,
,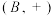 是否为加法群,并说明理由;
是否为加法群,并说明理由;(2)已知非空集合
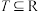 ,并且
,并且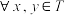 ,有
,有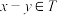 ,求证:
,求证: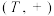 是一个加法群;
是一个加法群;(3)已知非空集合
 ,并且
,并且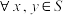 ,有
,有 ,求证:存在
,求证:存在 ,使得
,使得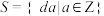 .
.
您最近一年使用:0次
2024-06-02更新
|
613次组卷
|
4卷引用:北京市顺义牛栏山第一中学2023-2024学年高一下学期期中考试数学试卷
北京市顺义牛栏山第一中学2023-2024学年高一下学期期中考试数学试卷(已下线)专题1 集合与常用逻辑为背景求参问题【练】(高一期中压轴专项)解答题广东省梅州市梅县东山中学2024-2025学年高一上学期10月月考数学试题(已下线)专题1 以集合为主体的新定义压轴大题(过关集训)
6 . 设集合 .定义:和集合
.定义:和集合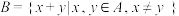 ,积集合
,积集合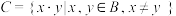 ,分别用
,分别用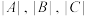 表示集合
表示集合 中元素的个数.
中元素的个数.
(1)若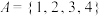 ,求集合
,求集合 ;
;
(2)若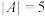 ,求
,求 的所有可能的值组成的集合;
的所有可能的值组成的集合;
(3)若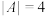 ,求证:
,求证: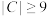 .
.
 .定义:和集合
.定义:和集合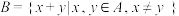 ,积集合
,积集合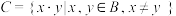 ,分别用
,分别用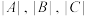 表示集合
表示集合 中元素的个数.
中元素的个数.(1)若
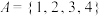 ,求集合
,求集合 ;
;(2)若
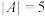 ,求
,求 的所有可能的值组成的集合;
的所有可能的值组成的集合;(3)若
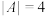 ,求证:
,求证: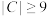 .
.
您最近一年使用:0次
2024-05-08更新
|
643次组卷
|
2卷引用:北京市和平街第一中学2024-2025学年高一上学期10月月考数学试题
名校
7 . 已知集合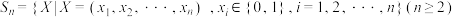 ,对于
,对于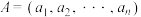 ,
,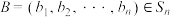 ,定义A与B的差为
,定义A与B的差为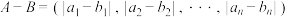 ,A与B之间的距离为
,A与B之间的距离为 .
.
(1)直接写出 中元素的个数,并证明:任意
中元素的个数,并证明:任意 ,有
,有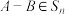 ;
;
(2)证明:任意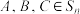 ,有
,有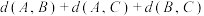 是偶数;
是偶数;
(3)证明: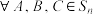 ,有
,有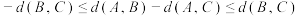 .
.
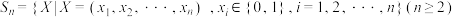 ,对于
,对于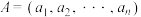 ,
,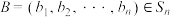 ,定义A与B的差为
,定义A与B的差为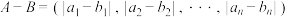 ,A与B之间的距离为
,A与B之间的距离为 .
.(1)直接写出
 中元素的个数,并证明:任意
中元素的个数,并证明:任意 ,有
,有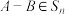 ;
;(2)证明:任意
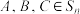 ,有
,有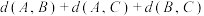 是偶数;
是偶数;(3)证明:
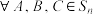 ,有
,有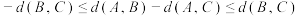 .
.
您最近一年使用:0次
8 . 设A,B为两个非空有限集合,定义 其中
其中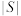 表示集合S的元素个数.某学校甲、乙、丙、丁四名同学从思想政治、历史、地理、物理、化学、生物这6门高中学业水平等级性考试科目中自主选择3门参加考试,设这四名同学的选考科目组成的集合分别为
表示集合S的元素个数.某学校甲、乙、丙、丁四名同学从思想政治、历史、地理、物理、化学、生物这6门高中学业水平等级性考试科目中自主选择3门参加考试,设这四名同学的选考科目组成的集合分别为 ,
, ,
, ,
,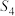 .已知
.已知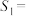 {物理,化学,生物},
{物理,化学,生物},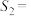 {地理,物理,化学},
{地理,物理,化学}, {思想政治,历史,地理},给出下列四个结论:
{思想政治,历史,地理},给出下列四个结论:
①若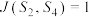 ,则
,则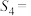 {思想政治,历史,生物};
{思想政治,历史,生物};
②若 ,则
,则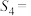 {地理,物理,化学};
{地理,物理,化学};
③若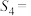 {思想政治,物理,生物},则
{思想政治,物理,生物},则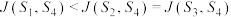 ;
;
④若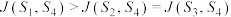 ,则
,则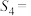 {思想政治,地理,化学}.
{思想政治,地理,化学}.
其中所有正确结论的序号是__________ .
 其中
其中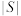 表示集合S的元素个数.某学校甲、乙、丙、丁四名同学从思想政治、历史、地理、物理、化学、生物这6门高中学业水平等级性考试科目中自主选择3门参加考试,设这四名同学的选考科目组成的集合分别为
表示集合S的元素个数.某学校甲、乙、丙、丁四名同学从思想政治、历史、地理、物理、化学、生物这6门高中学业水平等级性考试科目中自主选择3门参加考试,设这四名同学的选考科目组成的集合分别为 ,
, ,
, ,
,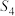 .已知
.已知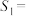 {物理,化学,生物},
{物理,化学,生物},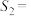 {地理,物理,化学},
{地理,物理,化学}, {思想政治,历史,地理},给出下列四个结论:
{思想政治,历史,地理},给出下列四个结论:①若
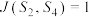 ,则
,则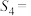 {思想政治,历史,生物};
{思想政治,历史,生物};②若
 ,则
,则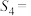 {地理,物理,化学};
{地理,物理,化学};③若
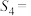 {思想政治,物理,生物},则
{思想政治,物理,生物},则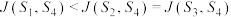 ;
;④若
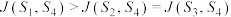 ,则
,则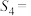 {思想政治,地理,化学}.
{思想政治,地理,化学}.其中所有正确结论的序号是
您最近一年使用:0次
2024-04-09更新
|
937次组卷
|
3卷引用:北京市东直门中学2024-2025学年高一上学期10月阶段考试数学试卷
名校
9 . 已知集合 (
( ,
, ),若存在数阵
),若存在数阵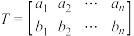 满足:
满足:
①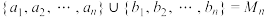 ;
;
② .
.
则称集合 为“好集合”,并称数阵
为“好集合”,并称数阵 为
为 的一个“好数阵”.
的一个“好数阵”.
(1)已知数阵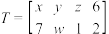 是
是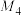 的一个“好数阵”,试写出
的一个“好数阵”,试写出 ,
, ,
, ,
, 的值;
的值;
(2)若集合 为“好集合”,证明:集合
为“好集合”,证明:集合 的“好数阵”必有偶数个;
的“好数阵”必有偶数个;
(3)判断 是否为“好集合”.若是,求出满足条件
是否为“好集合”.若是,求出满足条件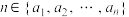 的所有“好数阵”;若不是,说明理由.
的所有“好数阵”;若不是,说明理由.
 (
( ,
, ),若存在数阵
),若存在数阵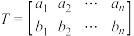 满足:
满足:①
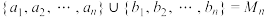 ;
;②
 .
.则称集合
 为“好集合”,并称数阵
为“好集合”,并称数阵 为
为 的一个“好数阵”.
的一个“好数阵”.(1)已知数阵
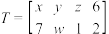 是
是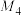 的一个“好数阵”,试写出
的一个“好数阵”,试写出 ,
, ,
, ,
, 的值;
的值;(2)若集合
 为“好集合”,证明:集合
为“好集合”,证明:集合 的“好数阵”必有偶数个;
的“好数阵”必有偶数个;(3)判断
 是否为“好集合”.若是,求出满足条件
是否为“好集合”.若是,求出满足条件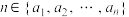 的所有“好数阵”;若不是,说明理由.
的所有“好数阵”;若不是,说明理由.
您最近一年使用:0次
2024-03-27更新
|
1958次组卷
|
8卷引用:北京市日坛中学2023-2024学年高一下学期期中考试数学试题
北京市日坛中学2023-2024学年高一下学期期中考试数学试题北京市丰台区2023-2024学年高三下学期综合练习(一)数学试题北京市第八十中学2023-2024学年高二下学期期中考试数学试题(已下线)压轴题01集合新定义、函数与导数13题型汇总 -1(已下线)拔高点突破01 集合背景下的新定义压轴解答题(四大题型)山东省A7联盟2024-2025学年高三上学期开学考试数学试题(已下线)专题1 以集合为主体的新定义压轴大题【讲】(已下线)专题7 线性代数、抽象代数与数论背景的新定义压轴大题(三)【讲】
名校
10 . 已知有 个连续正整数元素的有限集合
个连续正整数元素的有限集合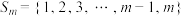 (
( ,
, ),记有序数对
),记有序数对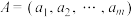 ,若对任意
,若对任意 ,
, ,
, ,
, 且
且 ,A同时满足下列条件,则称
,A同时满足下列条件,则称 为
为 元完备数对.
元完备数对.
条件①: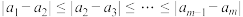 ;
;
条件②: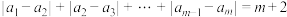 .
.
(1)试判断是否存在3元完备数对和4元完备数对,并说明理由;
(2)试证明不存在8元完备数对.
 个连续正整数元素的有限集合
个连续正整数元素的有限集合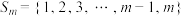 (
( ,
, ),记有序数对
),记有序数对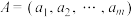 ,若对任意
,若对任意 ,
, ,
, ,
, 且
且 ,A同时满足下列条件,则称
,A同时满足下列条件,则称 为
为 元完备数对.
元完备数对.条件①:
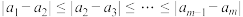 ;
;条件②:
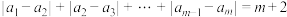 .
.(1)试判断是否存在3元完备数对和4元完备数对,并说明理由;
(2)试证明不存在8元完备数对.
您最近一年使用:0次
2024-02-23更新
|
500次组卷
|
2卷引用:北京市通州区2023-2024学年高一上学期期末质量检测数学试卷



