名校
解题方法
1 . 在解决实际问题时,往往会有不同的思路和方法,这些方法有些正确,有些错误;有些简洁,有些复杂
问题①设 ,集合
,集合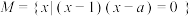 ,若
,若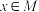 是
是 的充分条件,求:
的充分条件,求: 的取值集合
的取值集合
问题②:设 ,若
,若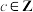 ,求证:
,求证: 和
和 至少有一个数是奇数
至少有一个数是奇数
(1)小明在解决问题①,他认为原问题等价于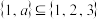 ,解得
,解得 的取值集合为
的取值集合为 ,张老师判断小明解题错误,请解出正确的
,张老师判断小明解题错误,请解出正确的 的取值集合并写出M集合的等价变形
的取值集合并写出M集合的等价变形
(2)小红认为既然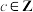 ,只需根据
,只需根据 是奇数还是偶数,分类讨论即可;小华则认为可以使用反证法解决问题,请你选择一种你认为更好的方法并证明
是奇数还是偶数,分类讨论即可;小华则认为可以使用反证法解决问题,请你选择一种你认为更好的方法并证明
问题①设
 ,集合
,集合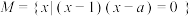 ,若
,若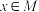 是
是 的充分条件,求:
的充分条件,求: 的取值集合
的取值集合问题②:设
 ,若
,若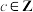 ,求证:
,求证: 和
和 至少有一个数是奇数
至少有一个数是奇数(1)小明在解决问题①,他认为原问题等价于
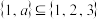 ,解得
,解得 的取值集合为
的取值集合为 ,张老师判断小明解题错误,请解出正确的
,张老师判断小明解题错误,请解出正确的 的取值集合并写出M集合的等价变形
的取值集合并写出M集合的等价变形(2)小红认为既然
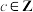 ,只需根据
,只需根据 是奇数还是偶数,分类讨论即可;小华则认为可以使用反证法解决问题,请你选择一种你认为更好的方法并证明
是奇数还是偶数,分类讨论即可;小华则认为可以使用反证法解决问题,请你选择一种你认为更好的方法并证明
您最近一年使用:0次
2 . 设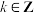 ,记关于
,记关于 与
与 的二元一次方程组
的二元一次方程组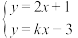 的解集为
的解集为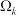 .
.
(1)求 ;
;
(2)是否存在 的值,使得
的值,使得 ?若存在,求出所有可能的
?若存在,求出所有可能的 值;若不存在,说明理由;
值;若不存在,说明理由;
(3)若 使得
使得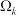 中的数对
中的数对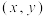 为正整数数对,即
为正整数数对,即 与
与 均为正整数,求
均为正整数,求 的值以及对应的
的值以及对应的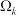 .
.
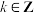 ,记关于
,记关于 与
与 的二元一次方程组
的二元一次方程组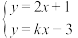 的解集为
的解集为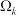 .
.(1)求
 ;
;(2)是否存在
 的值,使得
的值,使得 ?若存在,求出所有可能的
?若存在,求出所有可能的 值;若不存在,说明理由;
值;若不存在,说明理由;(3)若
 使得
使得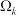 中的数对
中的数对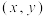 为正整数数对,即
为正整数数对,即 与
与 均为正整数,求
均为正整数,求 的值以及对应的
的值以及对应的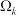 .
.
您最近一年使用:0次
2024-10-23更新
|
171次组卷
|
2卷引用:上海市控江中学2024-2025学年高一上学期9月月考数学试卷
名校
3 . 设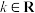 ,已知集合
,已知集合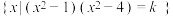 恰有四个非零元素,且它们在数轴上等距排列,则
恰有四个非零元素,且它们在数轴上等距排列,则
______ .
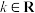 ,已知集合
,已知集合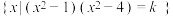 恰有四个非零元素,且它们在数轴上等距排列,则
恰有四个非零元素,且它们在数轴上等距排列,则
您最近一年使用:0次
2024-10-21更新
|
311次组卷
|
2卷引用:上海市市西中学2024-2025学年高一上学期9月月考数学试卷
名校
4 . 已知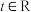 ,求满足下列条件的非空集合
,求满足下列条件的非空集合 中所有元素之和
中所有元素之和 .
.
(1)
(2)
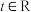 ,求满足下列条件的非空集合
,求满足下列条件的非空集合 中所有元素之和
中所有元素之和 .
.(1)

(2)

您最近一年使用:0次
名校
5 . 已知集合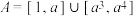 ,集合
,集合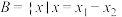 ,其中
,其中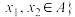 .若集合
.若集合 表示的区间为一个闭区间,则
表示的区间为一个闭区间,则 的取值范围为( )
的取值范围为( )
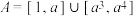 ,集合
,集合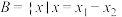 ,其中
,其中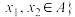 .若集合
.若集合 表示的区间为一个闭区间,则
表示的区间为一个闭区间,则 的取值范围为( )
的取值范围为( )A. 取遍任意大于 取遍任意大于 的实数 的实数 | B. |
C.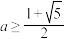 | D.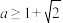 |
您最近一年使用:0次
6 . 设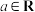 ,集合
,集合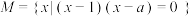 ,则总与
,则总与 相同的集合为( )
相同的集合为( )
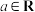 ,集合
,集合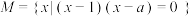 ,则总与
,则总与 相同的集合为( )
相同的集合为( )A.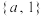 | B.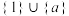 |
C.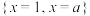 | D.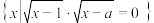 |
您最近一年使用:0次
2024-10-16更新
|
297次组卷
|
2卷引用:上海市控江中学2024-2025学年高一上学期9月月考数学试卷
名校
7 . 已知a、b都是正数,集合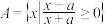 ,
,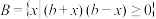 ,若任意的
,若任意的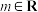 ,都有
,都有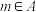 或
或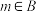 ,则下列结论中正确的是( )
,则下列结论中正确的是( )
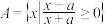 ,
,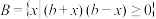 ,若任意的
,若任意的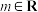 ,都有
,都有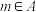 或
或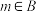 ,则下列结论中正确的是( )
,则下列结论中正确的是( )A. | B. | C. | D. |
您最近一年使用:0次
名校
8 . 已知 ,一个二次项系数为
,一个二次项系数为 的一元二次方程的两个不等实根分别为
的一元二次方程的两个不等实根分别为 和
和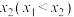 ,且满足
,且满足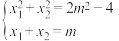 .
.
(1)直接写出该一元二次方程;
(2)若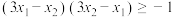 ,求
,求 的取值范围;
的取值范围;
(3)若 为正整数,记集合
为正整数,记集合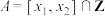 ,若
,若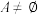 ,且
,且 中元素个数不超过
中元素个数不超过 ,求正整数
,求正整数 的取值范围.
的取值范围.
 ,一个二次项系数为
,一个二次项系数为 的一元二次方程的两个不等实根分别为
的一元二次方程的两个不等实根分别为 和
和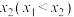 ,且满足
,且满足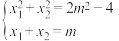 .
.(1)直接写出该一元二次方程;
(2)若
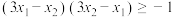 ,求
,求 的取值范围;
的取值范围;(3)若
 为正整数,记集合
为正整数,记集合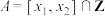 ,若
,若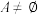 ,且
,且 中元素个数不超过
中元素个数不超过 ,求正整数
,求正整数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
9 . 记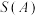 为集合
为集合 中所有元素之和,对于集合
中所有元素之和,对于集合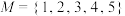 ,
,
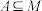 ,则所有
,则所有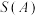 之和等于
之和等于__________ .
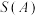 为集合
为集合 中所有元素之和,对于集合
中所有元素之和,对于集合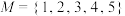 ,
,
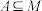 ,则所有
,则所有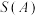 之和等于
之和等于
您最近一年使用:0次

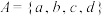 ,
,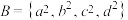 ,其中
,其中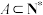 ,
, ,
,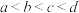 ,
, ,
, 中元素之和为124,且
中元素之和为124,且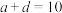 ,用列举法写出集合
,用列举法写出集合


