解题方法
1 . 已知函数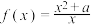 ,且
,且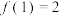 .
.
(1)求 ;
;
(2)求函数 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
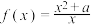 ,且
,且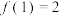 .
.(1)求
 ;
;(2)求函数
 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
您最近半年使用:0次
23-24高一上·河南·阶段练习
2 . 下列结论中正确的是( )
A.若函数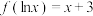 ,且 ,且 ,则 ,则 |
B.若 为奇函数,则 为奇函数,则 的解集为 的解集为 |
C.设 表示不超过 表示不超过 的最大整数,如 的最大整数,如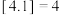 ,则不等式 ,则不等式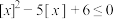 的解集是 的解集是 |
D.若函数 的定义域为 的定义域为 ,则 ,则 的取值范围是 的取值范围是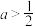 或 或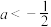 |
您最近半年使用:0次
名校
解题方法
3 . 函数 满足若
满足若 ,则
,则 ( )
( )
 满足若
满足若 ,则
,则 ( )
( )A.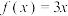 | B.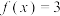 |
C.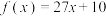 | D.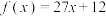 |
您最近半年使用:0次
2023-11-30更新
|
300次组卷
|
5卷引用:湖南省衡阳市祁东县育贤中学2023-2024学年高一上学期期中数学试题
湖南省衡阳市祁东县育贤中学2023-2024学年高一上学期期中数学试题(已下线)【第一练】3.1.2函数的表示法湖北省黄冈市浠水县第一中学2023-2024学年高一上学期期中数学试题(已下线)5.2 函数的表示方法-【题型分类归纳】(苏教版2019必修第一册)(已下线)专题03 函数的概念与性质1-2024年高一数学寒假作业单元合订本
23-24高一上·湖南·期中
名校
解题方法
4 . 已知函数 满足
满足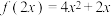 ,则( )
,则( )
 满足
满足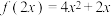 ,则( )
,则( )A. | B.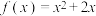 |
C.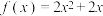 | D. |
您最近半年使用:0次
2023-11-16更新
|
177次组卷
|
3卷引用:湖南省三湘名校教育联盟2023-2024学年高一上学期11月期中联考数学试题
(已下线)湖南省三湘名校教育联盟2023-2024学年高一上学期11月期中联考数学试题山西省长治市部分学校2023-2024学年高一上学期11月质量检测数学试题河北郑口中学2023-2024学年高一下学期(寒假假期作业)开学检测数学试题
名校
解题方法
5 . 分别求满足下列条件的 的解析式:
的解析式:
(1)已知 ,求
,求 ;
;
(2)已知函数 是一次函数,若
是一次函数,若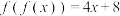 ,求
,求 ;
;
(3)已知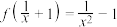 ,求
,求 .
.
 的解析式:
的解析式:(1)已知
 ,求
,求 ;
;(2)已知函数
 是一次函数,若
是一次函数,若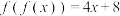 ,求
,求 ;
;(3)已知
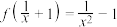 ,求
,求 .
.
您最近半年使用:0次
2023-10-18更新
|
1219次组卷
|
3卷引用:湖南省株洲市第二中学2023-2024学年高一上学期第一次阶段性测试数学试题
湖南省株洲市第二中学2023-2024学年高一上学期第一次阶段性测试数学试题湖南省株洲市第二中学2023-2024学年高一上学期第一次月考数学试题(已下线)第5章 函数概念与性质 章末题型归纳总结 (1)-【帮课堂】(苏教版2019必修第一册)
名校
解题方法
6 . 若函数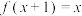 且
且 , 则
, 则 =( )
=( )
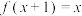 且
且 , 则
, 则 =( )
=( )| A.7 | B.8 | C.9 | D.10 |
您最近半年使用:0次
2023-10-10更新
|
721次组卷
|
2卷引用:湖南省长沙市平高集团六校联考2023-2024学年高一上学期期中联考数学试卷
名校
解题方法
7 . (1)已知 是一次函数,且满足
是一次函数,且满足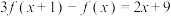 ,求
,求 的解析式;
的解析式;
(2)已知 ,求
,求 的解析式;
的解析式;
 是一次函数,且满足
是一次函数,且满足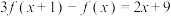 ,求
,求 的解析式;
的解析式;(2)已知
 ,求
,求 的解析式;
的解析式;
您最近半年使用:0次
2023-10-08更新
|
1597次组卷
|
8卷引用:湖南省永州市第一中学2023-2024学年高一上学期第一次月考数学试题
湖南省永州市第一中学2023-2024学年高一上学期第一次月考数学试题湖南省泸溪县第二中学2023-2024学年高一上学期第一次质量检测数学试题(已下线)第三章 函数的概念与性质(1a)速记·巧练(人教A版2019必修第一册)福建省莆田第二十五中学2023-2024学年高一上学期期中考试数学试题陕西省咸阳市高新一中2023-2024学年高一上学期第一次质量检测数学试题河北省唐山市迁安市2023-2024学年高一上学期期中考试数学试卷(已下线)第5章 函数概念与性质 章末题型归纳总结 (1)-【帮课堂】(苏教版2019必修第一册)(已下线)专题04 函数的概念及表示(2)-【寒假自学课】(苏教版2019)
名校
8 . 已知函数 在
在 上可导,且
上可导,且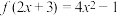 ,则
,则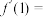
________ .
 在
在 上可导,且
上可导,且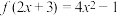 ,则
,则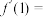
您最近半年使用:0次
2023-09-21更新
|
1239次组卷
|
10卷引用:湖南省衡阳市衡阳县第一中学2024届高三上学期11月月考数学试题
湖南省衡阳市衡阳县第一中学2024届高三上学期11月月考数学试题河北省保定市定州市第二中学2024届高三上学期9月月考数学试题辽宁省2023-2024学年2024届高三上学期一轮复习联考(一)数学试题江西省南昌大学附属中学等校2024届高三一轮复习联考(一)数学试题黑龙江省双鸭山市友谊县高级中学2023-2024学年高三上学期9月月考数学试题甘肃省张掖市某重点学校2024届高三上学期9月月考数学试题新疆百师联盟2024届高三上学期9月复习联考数学试题陕西省西安市阎良区关山中学2023-2024学年高三上学期第一次质量检测文科数学试题(已下线)河南省信阳市信阳高级中学2024届高三上学期测试(四)数学试题江西省宜春市宜丰中学2023-2024学年高二上学期1月期末考试数学试题
解题方法
9 . 已知 .
.
(1)求 的解析式及定义域;
的解析式及定义域;
(2)求 的值域,单调区间并判断奇偶性.(不要求写理由,只写结果)
的值域,单调区间并判断奇偶性.(不要求写理由,只写结果)
 .
.(1)求
 的解析式及定义域;
的解析式及定义域;(2)求
 的值域,单调区间并判断奇偶性.(不要求写理由,只写结果)
的值域,单调区间并判断奇偶性.(不要求写理由,只写结果)
您最近半年使用:0次
解题方法
10 . 已知函数 满足以下条件:①在区间
满足以下条件:①在区间 上单调递增;②对任意
上单调递增;②对任意 ,
, ,均有
,均有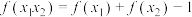 ,则
,则 的一个解析式为
的一个解析式为______ .
 满足以下条件:①在区间
满足以下条件:①在区间 上单调递增;②对任意
上单调递增;②对任意 ,
, ,均有
,均有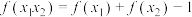 ,则
,则 的一个解析式为
的一个解析式为
您最近半年使用:0次



