1 . 已知函数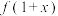 是定义域为
是定义域为 的偶函数,
的偶函数,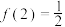 ,则
,则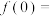
______ .
 是
是 的导函数,若对任意
的导函数,若对任意 ,使
,使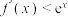 成立,则不等式
成立,则不等式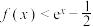 的解集为
的解集为______ .
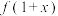 是定义域为
是定义域为 的偶函数,
的偶函数,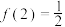 ,则
,则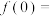
 是
是 的导函数,若对任意
的导函数,若对任意 ,使
,使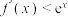 成立,则不等式
成立,则不等式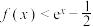 的解集为
的解集为
您最近半年使用:0次
名校
2 . 对于函数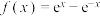 ,给出下列四个结论:
,给出下列四个结论:
① 是奇函数;
是奇函数;
②方程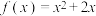 有且仅有1个实数根;
有且仅有1个实数根;
③ 在
在 上是增函数;
上是增函数;
④如果对任意 ,都有
,都有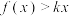 ,那么
,那么 的最大值为2.
的最大值为2.
其中正确结论的序号为__________ .
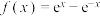 ,给出下列四个结论:
,给出下列四个结论:①
 是奇函数;
是奇函数;②方程
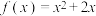 有且仅有1个实数根;
有且仅有1个实数根;③
 在
在 上是增函数;
上是增函数;④如果对任意
 ,都有
,都有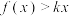 ,那么
,那么 的最大值为2.
的最大值为2.其中正确结论的序号为
您最近半年使用:0次
名校
3 . 函数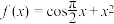 在区间
在区间 上的极值点的个数为
上的极值点的个数为______ .
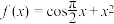 在区间
在区间 上的极值点的个数为
上的极值点的个数为
您最近半年使用:0次
名校
解题方法
4 . 请写出满足下列条件的一个函数 :
:______ .
①函数 的定义域为
的定义域为 ;
;
②对定义域内的任意实数 ,都有
,都有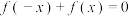 ;
;
③对定义域内的任意两个不等实数 ,
, ,都有
,都有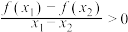 .
.
 :
:①函数
 的定义域为
的定义域为 ;
;②对定义域内的任意实数
 ,都有
,都有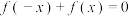 ;
;③对定义域内的任意两个不等实数
 ,
, ,都有
,都有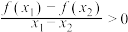 .
.
您最近半年使用:0次
5 . 阅读下面题目及其解答过程.
已知函数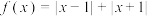 . .(1)求证:函数  是偶函数; 是偶函数;(2)求函数  的单调递增区间. 的单调递增区间.解:(1)因为函数  的定义域是 ① , 的定义域是 ① ,所以  ,都有 ,都有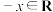 . .又因为  , ,所以 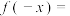 ② . ② .所以函数  是偶函数. 是偶函数.(2)当 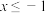 时, 时, , ,此时函数  在区间 在区间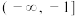 上单调递减. 上单调递减.当  时, 时, ③ . ③ .当  时, 时, ④ , ④ ,此时函数  在区间 ⑤ 上单调递增. 在区间 ⑤ 上单调递增.所以函数  的单调递增区间是 的单调递增区间是 . . |
| 空格序号 | 选项 | |
| ① | (A)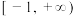 | (B) |
| ② | (A) | (B)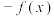 |
| ③ | (A)2 | (B) |
| ④ | (A)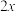 | (B)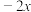 |
| ⑤ | (A) | (B) |
您最近半年使用:0次
名校
6 . 已知函数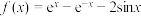 ,不等式
,不等式 对任意的
对任意的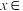
 恒成立,则
恒成立,则 的最大值为
的最大值为________ .
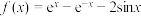 ,不等式
,不等式 对任意的
对任意的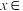
 恒成立,则
恒成立,则 的最大值为
的最大值为
您最近半年使用:0次
2023-12-08更新
|
563次组卷
|
3卷引用:湖北省武汉市第三中学2023-2024学年高二下学期3月月考数学试题
9-10高二下·福建福州·期末
名校
7 . 已知幂函数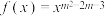 (其中,
(其中,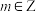 )为偶函数,且
)为偶函数,且 在
在 上单调递减,则
上单调递减,则 的值为
的值为_______ .
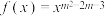 (其中,
(其中,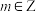 )为偶函数,且
)为偶函数,且 在
在 上单调递减,则
上单调递减,则 的值为
的值为
您最近半年使用:0次
2023-12-08更新
|
539次组卷
|
7卷引用:福建省福州八中09-10学年高二第二学期期末考试数学试题文科
(已下线)福建省福州八中09-10学年高二第二学期期末考试数学试题文科上海市曹杨二中2019-2020学年高三上学期期中数学试题甘肃省兰州市第五十五中学2022-2023学年高三上学期开学考试文科数学试题(已下线)江苏省南通市如皋市2023-2024学年高一上学期12月月考数学试题浙江省杭州市富阳区实验中学2023-2024学年高一上学期12月月考数学试题江苏省淮安市楚州中学2023-2024学年高一上学期12月教学质量调研数学试题江苏省南通市如皋市2023-2024学年高一上学期期中教学质量调研数学试题
23-24高三上·云南昆明·阶段练习
名校
8 . 定义在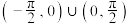 上的奇函数
上的奇函数 的导函数为
的导函数为 ,且当
,且当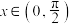 时,
时,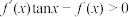 ,则不等式
,则不等式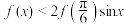 的解集为
的解集为_____________ .
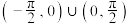 上的奇函数
上的奇函数 的导函数为
的导函数为 ,且当
,且当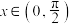 时,
时,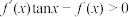 ,则不等式
,则不等式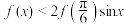 的解集为
的解集为
您最近半年使用:0次
2023-12-04更新
|
614次组卷
|
4卷引用:第五章 一元函数的导数及其应用(压轴题专练,精选34题)-2023-2024学年高二数学单元速记·巧练(人教A版2019选择性必修第二册)
(已下线)第五章 一元函数的导数及其应用(压轴题专练,精选34题)-2023-2024学年高二数学单元速记·巧练(人教A版2019选择性必修第二册)(已下线)专题09 利用导数研究函数的单调性(九大题型+过关检测专训)-2023-2024学年高二数学《重难点题型·高分突破》(人教A版2019选择性必修第二册)云南省昆明市第一中学2024届高三新课标第四次一轮复习检测数学试题广西名校2024届高三下学期高考模拟试卷数学信息卷
解题方法
9 . 设函数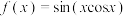 ,给出下列结论:
,给出下列结论:
① 是偶函数; ②当
是偶函数; ②当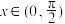 时,
时,
③ 是周期函数; ④
是周期函数; ④ 存在无数个零点;
存在无数个零点;
其中正确结论的序号是______ (写出所有正确结论的序号)
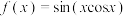 ,给出下列结论:
,给出下列结论:①
 是偶函数; ②当
是偶函数; ②当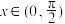 时,
时,
③
 是周期函数; ④
是周期函数; ④ 存在无数个零点;
存在无数个零点;其中正确结论的序号是
您最近半年使用:0次
名校
解题方法
10 . 已知函数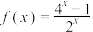 ,则
,则 的解集为
的解集为_________ .
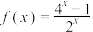 ,则
,则 的解集为
的解集为
您最近半年使用:0次



