名校
解题方法
1 . 高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,用其名字命名的“高斯函数”为:设x∈R,用[x]表示不超过x的最大整数,则y=[x]称为高斯函数.例如:[-0.5]=-1,[1.5]=1.已知函数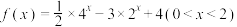 ,则函数y=[f(x)]的值域为( )
,则函数y=[f(x)]的值域为( )
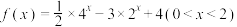 ,则函数y=[f(x)]的值域为( )
,则函数y=[f(x)]的值域为( )A.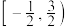 | B.{-1,0,1} |
| C.{-1,0,1,2} | D.{0,1,2} |
您最近半年使用:0次
2021-12-18更新
|
482次组卷
|
3卷引用:吉林省吉林市第一中学2021-2022学年高二下学期期中考试数学试题(平行班)
吉林省吉林市第一中学2021-2022学年高二下学期期中考试数学试题(平行班)江苏省无锡市市北高级中学2022-2023学年高一上学期期中数学试题(已下线)第五章 函数概念与性质(选拔卷)-【单元测试】2021-2022学年高一数学尖子生选拔卷(苏教版2019必修第一册)
名校
2 . 1.已知函数 ,函数
,函数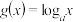 (
( 且
且 )
)
(1)求函数 的值域;
的值域;
(2)已知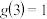 ,若不等式
,若不等式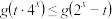 在
在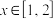 上有解,求实数
上有解,求实数 的最大值.
的最大值.
 ,函数
,函数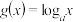 (
( 且
且 )
)(1)求函数
 的值域;
的值域;(2)已知
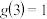 ,若不等式
,若不等式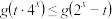 在
在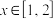 上有解,求实数
上有解,求实数 的最大值.
的最大值.
您最近半年使用:0次
2021-12-04更新
|
1381次组卷
|
5卷引用:吉林省长春市第二中学2021-2022学年高一上学期期中数学试题
名校
解题方法
3 . 已知命题 ,使得
,使得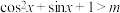 ,若命题p是假命题,则实数m的取值范围是
,若命题p是假命题,则实数m的取值范围是________ .
 ,使得
,使得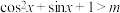 ,若命题p是假命题,则实数m的取值范围是
,若命题p是假命题,则实数m的取值范围是
您最近半年使用:0次
2020-05-08更新
|
498次组卷
|
2卷引用:吉林省长春市第二实验中学2020-2021学年高二上学期期中考试数学(理)试题
名校
解题方法
4 . 已知函数 [1, 2].
[1, 2].
(1)求函数 的值域;
的值域;
(2)设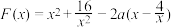
 ,
,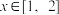 ,
, ,求函数
,求函数 的最小值
的最小值 .
.
(3)对(2)中的 ,若不等式
,若不等式 对于任意的
对于任意的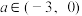 时恒成立,求实数
时恒成立,求实数 的取值范围.
的取值范围.
 [1, 2].
[1, 2].(1)求函数
 的值域;
的值域;(2)设
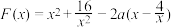
 ,
,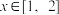 ,
, ,求函数
,求函数 的最小值
的最小值 .
.(3)对(2)中的
 ,若不等式
,若不等式 对于任意的
对于任意的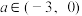 时恒成立,求实数
时恒成立,求实数 的取值范围.
的取值范围.
您最近半年使用:0次
2020-11-12更新
|
435次组卷
|
12卷引用:吉林省长春市长春外国语学校2020-2021学年高一上学期期中考试数学试题
吉林省长春市长春外国语学校2020-2021学年高一上学期期中考试数学试题江苏省无锡市太湖高级中学2020-2021学年高一上学期期中复习卷(1)数学试题江苏省无锡市江阴市第一中学2020-2021学年高一上学期期中数学试题江苏省淮安市盱眙中学2020-2021学年高一上学期期中数学试题江苏省镇江中学2022-2023学年高一上学期期中数学试题(已下线)江苏省如皋市2017-2018学年高一上学期教学质量调研数学试题安徽省淮南市第一中学2019-2020学年高一上学期第一次段考数学试题江苏省连云港市东海高级中学2019-2020学年高一上学期第一次月考数学试题(已下线)【新东方】2019新中心五地132高中数学重庆市缙云教育联盟2020-2021学年高二上学期10月月考数学试题江苏省苏州市昆山中学2020-2021学年高一上学期模块测试一数学试题江苏省连云港市板浦高级中学2020-2021学年高三上学期第一次月考数学试题
解题方法
5 . 已知函数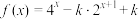 ,
, .
.
(1)当 时,求
时,求 的值域;
的值域;
(2)若 的最小值为
的最小值为 ,求k的值.
,求k的值.
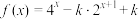 ,
, .
.(1)当
 时,求
时,求 的值域;
的值域;(2)若
 的最小值为
的最小值为 ,求k的值.
,求k的值.
您最近半年使用:0次
2020-02-23更新
|
1018次组卷
|
5卷引用:吉林省白城市通榆县第一中学2019-2020学年高一上学期期中数学试题
6 . 函数 (
(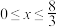 )的最大值是( )
)的最大值是( )
 (
(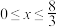 )的最大值是( )
)的最大值是( )| A.0 | B.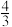 | C.4 | D.16 |
您最近半年使用:0次
名校
7 . 函数 的图象与函数
的图象与函数 的图象关于直线
的图象关于直线 对称,则
对称,则 的单调递减区间为( )
的单调递减区间为( )
 的图象与函数
的图象与函数 的图象关于直线
的图象关于直线 对称,则
对称,则 的单调递减区间为( )
的单调递减区间为( )A. | B. | C. | D. |
您最近半年使用:0次
名校
8 . 已知函数 ,
,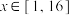
(1)求函数 的值域.
的值域.
(2)设 ,求
,求 的最值及相应的
的最值及相应的 的值.
的值.
 ,
,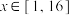
(1)求函数
 的值域.
的值域.(2)设
 ,求
,求 的最值及相应的
的最值及相应的 的值.
的值.
您最近半年使用:0次
2019-11-01更新
|
1344次组卷
|
4卷引用:吉林省吉化第一高级中学校2019-2020学年高一上学期期中数学试题
名校
9 . 设函数 ,
, .
.
(1)求函数 的解析式;
的解析式;
(2)设 ,
, 在
在 上的最小值为
上的最小值为 ,求
,求 .
.
 ,
, .
.(1)求函数
 的解析式;
的解析式;(2)设
 ,
, 在
在 上的最小值为
上的最小值为 ,求
,求 .
.
您最近半年使用:0次
2019-06-19更新
|
3992次组卷
|
12卷引用:吉林省长春市农安县2022-2023学年高一上学期期中数学试题
吉林省长春市农安县2022-2023学年高一上学期期中数学试题【全国百强校】云南省曲靖市会泽县茚旺高级中学2018-2019学年高一下学期期中考试数学试题吉林省延吉市延边第二中学2019-2020学年高二上学期第一次月考数学试题吉林省延边二中2019-2020学年高一上学期第一次月考数学试题黑龙江省鹤岗市第一中学2019-2020学年高一上学期期中数学(理)试题河南省鹤壁市淇滨高级中学2019-2020学年高一上学期期中数学试题湖南省衡阳市衡阳县第四中学2023-2024学年高一上学期11月期中测试数学试题(A卷)(已下线)2019年7月28日 《每日一题》2020年理数一轮复习-每周一测(已下线)2019年7月28日 《每日一题》2020年文数一轮复习-每周一测安徽省滁州市明光中学2019-2020学年高一上学期第一次月考数学试题河北省衡水市第十四中学2020-2021学年高一下学期摸底考试数学试题3.3 指数函数同步课时作业-2021-2022学年高一上学期数学北师大版(2019)必修第一册
名校
10 . 已知定义在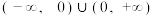 上的奇函数
上的奇函数 满足
满足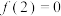 ,且在
,且在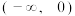 上是增函数;又定义行列式
上是增函数;又定义行列式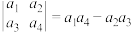 ; 函数
; 函数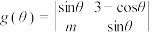 (其中
(其中 )
)
(1)证明: 函数 在
在 上也是增函数;
上也是增函数;
(2)若函数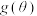 的最大值为
的最大值为 ,求
,求 的值;
的值;
(3)若记集合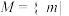 恒有
恒有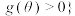 ,
, 恒有
恒有 ,求满足
,求满足 的
的 的取值范围.
的取值范围.
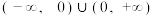 上的奇函数
上的奇函数 满足
满足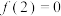 ,且在
,且在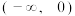 上是增函数;又定义行列式
上是增函数;又定义行列式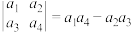 ; 函数
; 函数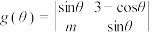 (其中
(其中 )
)(1)证明: 函数
 在
在 上也是增函数;
上也是增函数;(2)若函数
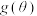 的最大值为
的最大值为 ,求
,求 的值;
的值;(3)若记集合
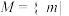 恒有
恒有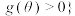 ,
, 恒有
恒有 ,求满足
,求满足 的
的 的取值范围.
的取值范围.
您最近半年使用:0次



