名校
1 . 已知函数 .
.
(1)当 时,解不等式
时,解不等式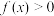 ;
;
(2)若关于 的方程
的方程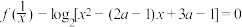 在区间
在区间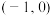 上恰有一个实数解,求
上恰有一个实数解,求 的取值范围;
的取值范围;
 .
.(1)当
 时,解不等式
时,解不等式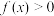 ;
;(2)若关于
 的方程
的方程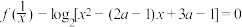 在区间
在区间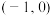 上恰有一个实数解,求
上恰有一个实数解,求 的取值范围;
的取值范围;
您最近一年使用:0次
2022-12-10更新
|
430次组卷
|
4卷引用:辽宁省沈阳市沈抚育才实验学校2022-2023学年高一上学期期末数学试题
名校
2 . 函数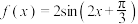 ,若
,若 的图象向左平移
的图象向左平移 个单位得到
个单位得到 .
.
(1)求不等式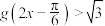 的解集;
的解集;
(2)若函数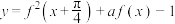 的最大值为9,求
的最大值为9,求 的值;
的值;
(3)若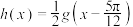 ,方程
,方程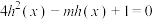 在
在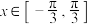 内有一个解,求实数
内有一个解,求实数 的取值范围.
的取值范围.
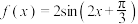 ,若
,若 的图象向左平移
的图象向左平移 个单位得到
个单位得到 .
.(1)求不等式
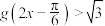 的解集;
的解集;(2)若函数
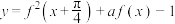 的最大值为9,求
的最大值为9,求 的值;
的值;(3)若
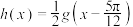 ,方程
,方程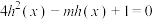 在
在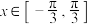 内有一个解,求实数
内有一个解,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
3 . 已知函数 .
.
(1)当 时:
时:
①解关于 的不等式
的不等式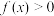 ;
;
②证明: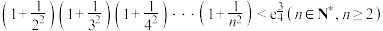 ;
;
(2)若函数 恰有三个不同的零点,求实数
恰有三个不同的零点,求实数 的取值范围.
的取值范围.
 .
.(1)当
 时:
时:①解关于
 的不等式
的不等式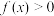 ;
;②证明:
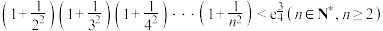 ;
;(2)若函数
 恰有三个不同的零点,求实数
恰有三个不同的零点,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2022-01-11更新
|
1367次组卷
|
4卷引用:辽宁省大连育明高级中学2023-2024学年高三下学期第一次模拟考试数学试卷
4 . 已知函数 为
为 的极值点.
的极值点.
(1)求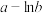 的最小值;
的最小值;
(2)若关于 的方程
的方程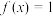 有且仅有两个实数解,求
有且仅有两个实数解,求 的取值范围.
的取值范围.
 为
为 的极值点.
的极值点.(1)求
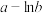 的最小值;
的最小值;(2)若关于
 的方程
的方程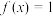 有且仅有两个实数解,求
有且仅有两个实数解,求 的取值范围.
的取值范围.
您最近一年使用:0次
2024-05-14更新
|
785次组卷
|
3卷引用:2024年辽宁省普通高等学校招生全国统一考试(模拟1)数学试题
名校
5 . 已知向量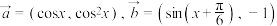 .设函数
.设函数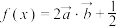
(1)求函数 的解析式及其单调增区间;
的解析式及其单调增区间;
(2)设 ,若方程
,若方程 在
在 上有两个不同的解
上有两个不同的解 ,求实数m的取值范围,并求
,求实数m的取值范围,并求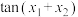 的值.
的值.
(3)若将 的图象上的所有点向左平移
的图象上的所有点向左平移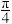 个单位,再把所得图象上所有点的横坐标伸长为原来的2倍(纵坐标不变),得到函数
个单位,再把所得图象上所有点的横坐标伸长为原来的2倍(纵坐标不变),得到函数 的图象.当
的图象.当 (其中
(其中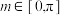 )时,记函数
)时,记函数 的最大值与最小值分别为
的最大值与最小值分别为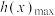 与
与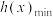 ,设
,设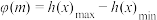 求函数
求函数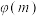 的解析式.
的解析式.
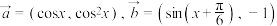 .设函数
.设函数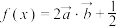
(1)求函数
 的解析式及其单调增区间;
的解析式及其单调增区间;(2)设
 ,若方程
,若方程 在
在 上有两个不同的解
上有两个不同的解 ,求实数m的取值范围,并求
,求实数m的取值范围,并求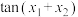 的值.
的值.(3)若将
 的图象上的所有点向左平移
的图象上的所有点向左平移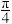 个单位,再把所得图象上所有点的横坐标伸长为原来的2倍(纵坐标不变),得到函数
个单位,再把所得图象上所有点的横坐标伸长为原来的2倍(纵坐标不变),得到函数 的图象.当
的图象.当 (其中
(其中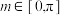 )时,记函数
)时,记函数 的最大值与最小值分别为
的最大值与最小值分别为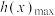 与
与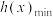 ,设
,设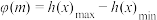 求函数
求函数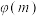 的解析式.
的解析式.
您最近一年使用:0次
6 . 已知函数 .
.
(1)求 的单调递增区间;
的单调递增区间;
(2)求 在区间
在区间 上的最大值和最小值;
上的最大值和最小值;
(3)若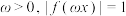 在区间
在区间 上有且仅有一个解,求
上有且仅有一个解,求 的取值范围.
的取值范围.
 .
.(1)求
 的单调递增区间;
的单调递增区间;(2)求
 在区间
在区间 上的最大值和最小值;
上的最大值和最小值;(3)若
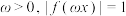 在区间
在区间 上有且仅有一个解,求
上有且仅有一个解,求 的取值范围.
的取值范围.
您最近一年使用:0次
2024-04-24更新
|
229次组卷
|
2卷引用:辽宁省大连市一0三中学2023-2024学年高一下学期4月月考数学试卷
名校
解题方法
7 . 已知函数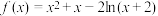 .
.
(1)若关于 的方程
的方程 在区间
在区间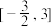 上恰有2个不同的实数解,求
上恰有2个不同的实数解,求 的取值范围;
的取值范围;
(2)设函数 ,若
,若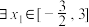 ,对
,对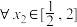 总有
总有 成立,求
成立,求 的取值范围.
的取值范围.
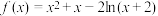 .
.(1)若关于
 的方程
的方程 在区间
在区间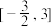 上恰有2个不同的实数解,求
上恰有2个不同的实数解,求 的取值范围;
的取值范围;(2)设函数
 ,若
,若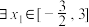 ,对
,对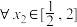 总有
总有 成立,求
成立,求 的取值范围.
的取值范围.
您最近一年使用:0次
2023-07-09更新
|
513次组卷
|
2卷引用:辽宁省沈阳市东北育才学校少儿部2023-2024学年高三上学期第一次模拟考试数学试题
名校
解题方法
8 . 已知函数 的最小正周期为
的最小正周期为 .
.
(1)求 的解析式;
的解析式;
(2)若关于x的方程 在区间
在区间 上有相异两解
上有相异两解
求:①实数a的取值范围;
②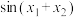 的值.
的值.
 的最小正周期为
的最小正周期为 .
.(1)求
 的解析式;
的解析式;(2)若关于x的方程
 在区间
在区间 上有相异两解
上有相异两解
求:①实数a的取值范围;
②
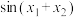 的值.
的值.
您最近一年使用:0次
2023-02-25更新
|
1703次组卷
|
11卷引用:辽宁省朝阳市建平县实验中学2022-2023学年高一下学期期末考试数学试题
辽宁省朝阳市建平县实验中学2022-2023学年高一下学期期末考试数学试题河南省商开大联考2022~2023学年高一上学期期末考试数学试题重庆市第一中学校2022-2023学年高一下学期第一次月考(3月)数学试题湖北省宜昌市协作体2022-2023学年高一下学期期中联考数学试题江西师范大学附属中学2022-2023学年高一下学期期中考试数学试题安徽省六安市毛坦厂中学2022-2023学年高一下学期期中考试数学试题(已下线)专题7 大题分类练(向量的数量积与三角恒等变换)(拔高能力练)(人教B)内蒙古乌兰浩特市第四中学2022-2023学年高一下学期第三次月考数学试题四川省泸县第五中学2022-2023学年高一下学期4月月考数学试题广东省深圳市南头中学2024届高三上学期第二次月考数学试题(已下线)第五章 三角函数(32类知识归纳+38类题型突破)(6) -速记·巧练(人教A版2019必修第一册)
名校
解题方法
9 . 已知点 ,
,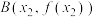 是函数
是函数
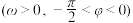 图象上的任意两点,且角
图象上的任意两点,且角 的终边经过点
的终边经过点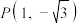 ,若
,若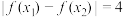 时,
时, 的最小值为
的最小值为 .
.
(1)求函数 的解析式;
的解析式;
(2)若方程 在
在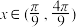 内有两个不同的解,求实数
内有两个不同的解,求实数 的取值范围.
的取值范围.
 ,
,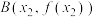 是函数
是函数
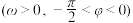 图象上的任意两点,且角
图象上的任意两点,且角 的终边经过点
的终边经过点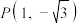 ,若
,若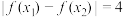 时,
时, 的最小值为
的最小值为 .
.(1)求函数
 的解析式;
的解析式;(2)若方程
 在
在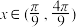 内有两个不同的解,求实数
内有两个不同的解,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2022-03-03更新
|
873次组卷
|
12卷引用:辽宁省沈阳市第一二〇中学2020-2021学年高一上学期4月数学月考试题
辽宁省沈阳市第一二〇中学2020-2021学年高一上学期4月数学月考试题2015-2016学年浙江省杭州二中高一上期末数学试卷甘肃省天水市第一中学2019年高三上学期10月月考数学(理)试题甘肃省天水市第一中学2020届高三上学期第二次考试数学(理)试题湖南省长沙市长沙县实验中学2019-2020学年高一下学期期末数学试题(已下线)专题20 三角函数中的压轴题(二)-【尖子生专用】2021-2022学年高一数学考点培优训练(人教A版2019必修第一册)(已下线)思想03 数形结合思想(练)--第三篇 思想方法篇-《2022年高考数学二轮复习讲练测(新高考·全国卷)》江西省宜春市上高二中2021-2022学年高一3月第六次月考试题江西省宜春市万载中学2021-2022学年高一(普通班)3月月考数学试题河南省南阳市第六完全学校高级中学2021-2022学年高一下学期第三次考试数学试题 江西省抚州市金溪县第一中学2022-2023学年高一下学期第一次月考数学试题江西省抚州市临川区第十六中学2023-2024学年高一下学期期中考试数学试题(文化)
名校
解题方法
10 . 已知函数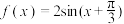 .
.
(1)若不等式 对任意
对任意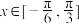 恒成立,求整数m的最大值;
恒成立,求整数m的最大值;
(2)若函数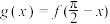 ,将函数
,将函数 的图象上各点的横坐标缩短到原来的
的图象上各点的横坐标缩短到原来的 倍(纵坐标不变),再向右平移
倍(纵坐标不变),再向右平移 个单位,得到函数
个单位,得到函数 的图象,若关于x的方程
的图象,若关于x的方程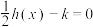 在
在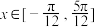 上有2个不同实数解,求实数k的取值范围.
上有2个不同实数解,求实数k的取值范围.
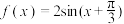 .
.(1)若不等式
 对任意
对任意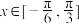 恒成立,求整数m的最大值;
恒成立,求整数m的最大值;(2)若函数
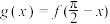 ,将函数
,将函数 的图象上各点的横坐标缩短到原来的
的图象上各点的横坐标缩短到原来的 倍(纵坐标不变),再向右平移
倍(纵坐标不变),再向右平移 个单位,得到函数
个单位,得到函数 的图象,若关于x的方程
的图象,若关于x的方程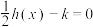 在
在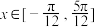 上有2个不同实数解,求实数k的取值范围.
上有2个不同实数解,求实数k的取值范围.
您最近一年使用:0次
2022-06-10更新
|
1671次组卷
|
8卷引用:辽宁省锦州市辽西育明高级中学2022-2023学年高一下学期第一次阶段性数学试题
辽宁省锦州市辽西育明高级中学2022-2023学年高一下学期第一次阶段性数学试题山东省青岛市第十九中学2021-2022学年高一下学期期中考试数学试题(已下线)第08讲:第四章 三角函数(测)(提高卷)-2023年高考数学一轮复习讲练测(新教材新高考)(已下线)专题4-4 三角函数与解三角形大题综合归类-1(已下线)专题06 三角函数(讲义)-2河南省驻马店高级中学2022-2023学年高一下学期第一次月考数学试题(已下线)第5章 三角函数(基础、典型、易错、压轴)分类专项训练(2)(已下线)第30讲 三角函数解答题7种常见题型总结(2)-【同步题型讲义】(人教A版2019必修第一册)



