名校
1 . 设 为空间中两直线的夹角,则在平面直角坐标系中方程
为空间中两直线的夹角,则在平面直角坐标系中方程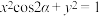 表示的曲线可能是( )
表示的曲线可能是( )
 为空间中两直线的夹角,则在平面直角坐标系中方程
为空间中两直线的夹角,则在平面直角坐标系中方程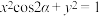 表示的曲线可能是( )
表示的曲线可能是( )| A.两条相交直线 | B.圆 |
| C.焦点在x轴上的椭圆 | D.焦点在x轴上的双曲线 |
您最近一年使用:0次
2024-02-05更新
|
233次组卷
|
4卷引用:湖北省荆州市八县市区2023-2024学年高二上学期1月期末联合考试数学试题
名校
解题方法
2 . 写出一个同时满足下列三个性质的函数:
__________ .
① 为偶函数;②
为偶函数;② 关于
关于 中心对称;③
中心对称;③ 在
在 上的最大值为3.
上的最大值为3.

①
 为偶函数;②
为偶函数;② 关于
关于 中心对称;③
中心对称;③ 在
在 上的最大值为3.
上的最大值为3.
您最近一年使用:0次
2023-03-24更新
|
196次组卷
|
2卷引用:湖北省恩施州高中教育联盟2022-2023学年高一下学期期中数学试题
解题方法
3 . 如图,点 是半径为
是半径为 的半圆弧上的动点,半圆的圆心为
的半圆弧上的动点,半圆的圆心为 ,
,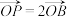 ,则
,则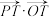 的最大值为( )
的最大值为( )

 是半径为
是半径为 的半圆弧上的动点,半圆的圆心为
的半圆弧上的动点,半圆的圆心为 ,
,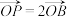 ,则
,则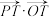 的最大值为( )
的最大值为( )
A. | B. | C.3 | D.4 |
您最近一年使用:0次
2022-06-23更新
|
401次组卷
|
3卷引用:湖北省十堰市柳林中学2022-2023学年高一下学期期中数学试题
4 . 已知偶函数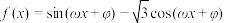 (
( ,
, )在
)在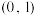 上恰有2个极大值点,则实数
上恰有2个极大值点,则实数 的取值范围为( )
的取值范围为( )
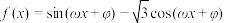 (
( ,
, )在
)在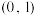 上恰有2个极大值点,则实数
上恰有2个极大值点,则实数 的取值范围为( )
的取值范围为( )A. | B.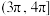 |
C.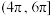 | D.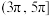 |
您最近一年使用:0次
2022-05-25更新
|
1458次组卷
|
8卷引用:湖北省武汉市2022届高三下学期五月模拟(二)数学试题
湖北省武汉市2022届高三下学期五月模拟(二)数学试题(已下线)专题04 三角函数(已下线)专题11 三角函数的图象与性质(ω的取值范围)-3(已下线)专题11 三角函数的图象与性质(ω的取值范围)-2(已下线)专题13 ω的取值范围与最值问题-2(已下线)第四章 三角函数与解三角形 第五节 y=Asin(wx+b) 的图象与性质(讲)(已下线)第四章 三角函数与解三角形 第五节 y=Asin(wx+b) 的图象与性质(大一轮)【讲-提升版】(已下线)【讲】第四节 三角函数的图象性质(北京专版)
名校
解题方法
5 . 已知函数 ,其中
,其中 表示不超过实数
表示不超过实数 的最大整数,关于
的最大整数,关于 有下述四个结论,其中错误的结论是( )
有下述四个结论,其中错误的结论是( )
 ,其中
,其中 表示不超过实数
表示不超过实数 的最大整数,关于
的最大整数,关于 有下述四个结论,其中错误的结论是( )
有下述四个结论,其中错误的结论是( )A. 的一个周期是 的一个周期是 |
B. 是偶函数 是偶函数 |
C. 在区间 在区间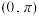 上单调递减 上单调递减 |
D. 的最大值大于 的最大值大于 |
您最近一年使用:0次
2022-05-21更新
|
934次组卷
|
3卷引用:湖北省恩施高中、荆州中学等四校2022届高三下学期5月联考数学试题
名校
解题方法
6 . 在平面直角坐标系中,O为坐标原点,已知向量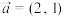 且A(1,0),B(cos θ,t).
且A(1,0),B(cos θ,t).
(1)若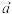 ∥
∥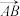 ,且|
,且|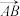 |=
|=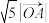 ,求向量
,求向量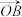 的坐标;
的坐标;
(2)若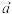 ∥
∥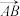 ,求y=cos2θ-cos θ+t2的最小值.
,求y=cos2θ-cos θ+t2的最小值.
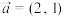 且A(1,0),B(cos θ,t).
且A(1,0),B(cos θ,t).(1)若
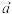 ∥
∥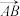 ,且|
,且|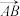 |=
|=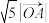 ,求向量
,求向量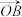 的坐标;
的坐标;(2)若
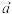 ∥
∥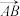 ,求y=cos2θ-cos θ+t2的最小值.
,求y=cos2θ-cos θ+t2的最小值.
您最近一年使用:0次
2022-04-19更新
|
448次组卷
|
11卷引用:【市级联考】湖北省天门市、潜江市、应城市2018-2019学年高一下学期期中联考数学试题
【市级联考】湖北省天门市、潜江市、应城市2018-2019学年高一下学期期中联考数学试题【全国百强校】黑龙江省大庆实验中学2018-2019学年高一下学期开学考试数学试题【全国百强校】宁夏回族自治区银川一中2018-2019学年高一下学期期中考试数学试题【市级联考】吉林省舒兰市2018-2019学年高一下学期期中考试数学试题江苏省南通市如东高级中学2019-2020学年高一上学期12月月考数学试题吉林省吉化第一高级中学校2018-2019学年高一下学期期中考试数学试题广东省潮州市2019-2020学年高一下学期期中数学试题(已下线)【新东方】双师202高一下江苏省南京市中华中学2021-2022学年高一下学期4月阶段检测数学试题黑龙江省哈尔滨市第六中学校2021-2022学年高一下学期期中考试数学试题黑龙江哈尔滨市第六中学校2023-2024学年高一下学期期中考试数学试题
名校
解题方法
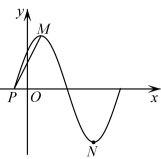
7 . 函数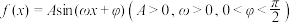 在一个周期内的图象如图所示,O为坐标原点,M,N为图象上相邻的最高点与最低点,
在一个周期内的图象如图所示,O为坐标原点,M,N为图象上相邻的最高点与最低点,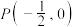 也在该图象上,且
也在该图象上,且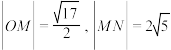 .
.
(1)求 的解析式;
的解析式;
(2) 的图象向左平移1个单位后得到
的图象向左平移1个单位后得到 的图象,试求函数
的图象,试求函数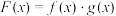 在
在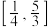 上的最大值和最小值.
上的最大值和最小值.
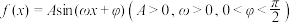 在一个周期内的图象如图所示,O为坐标原点,M,N为图象上相邻的最高点与最低点,
在一个周期内的图象如图所示,O为坐标原点,M,N为图象上相邻的最高点与最低点,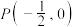 也在该图象上,且
也在该图象上,且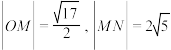 .
.
(1)求
 的解析式;
的解析式;(2)
 的图象向左平移1个单位后得到
的图象向左平移1个单位后得到 的图象,试求函数
的图象,试求函数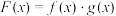 在
在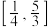 上的最大值和最小值.
上的最大值和最小值.
您最近一年使用:0次
2022-02-15更新
|
711次组卷
|
4卷引用:湖北省襄阳市第四中学2021-2022学年高一下学期2月考试数学试题
名校
8 . 已知函数 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)求函数 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
 .
.(1)求函数
 的单调递增区间;
的单调递增区间;(2)求函数
 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
您最近一年使用:0次
2022-01-27更新
|
975次组卷
|
5卷引用:湖北省2021-2022学年高一上学期期末调考数学试题
9 . 已知函数 .
.
(1)求 的单调增区间;
的单调增区间;
(2)当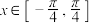 ,求
,求 的值域,并求取得最小值时x的取值集合.
的值域,并求取得最小值时x的取值集合.
 .
.(1)求
 的单调增区间;
的单调增区间;(2)当
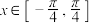 ,求
,求 的值域,并求取得最小值时x的取值集合.
的值域,并求取得最小值时x的取值集合.
您最近一年使用:0次
名校
10 . 已知函数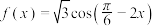 .
.
(1)求函数 的单调区间;
的单调区间;
(2)求函数 在区间
在区间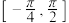 上的最小值和最大值.
上的最小值和最大值.
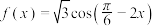 .
.(1)求函数
 的单调区间;
的单调区间;(2)求函数
 在区间
在区间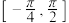 上的最小值和最大值.
上的最小值和最大值.
您最近一年使用:0次
2022-01-17更新
|
957次组卷
|
5卷引用:湖北省黄冈市2021-2022学年高一上学期期末数学试题



