名校
1 . 已知向量  和
和  ,则
,则 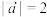 ,
, ,
, 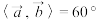 求:
求:
(1) 的值;
的值;
(2)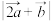 的值;
的值;
(3)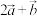 与
与  的夹角θ的余弦值.
的夹角θ的余弦值.
 和
和  ,则
,则 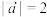 ,
, ,
, 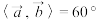 求:
求:(1)
 的值;
的值;(2)
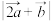 的值;
的值;(3)
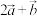 与
与  的夹角θ的余弦值.
的夹角θ的余弦值.
您最近一年使用:0次
2024-02-23更新
|
7012次组卷
|
27卷引用:山东省聊城颐中外国语学校2023-2024学年高一下学期第一次质量检测数学试题
山东省聊城颐中外国语学校2023-2024学年高一下学期第一次质量检测数学试题山东省青岛超银高级中学2023-2024学年高一下学期4月月考数学试卷北京市第四中学顺义分校2021-2022学年高一下学期期中考试数学试卷河北省唐山市第五中学2023-2024学年高一下学期开学考试数学试题(已下线)8.1.2向量数量积的运算律-同步精品课堂(人教B版2019必修第三册)(已下线)高一数学第一次月考模拟卷(范围:平面向量+复数)-同步精讲精练宝典河北省沧州市献县实验中学2023-2024学年高一下学期3月月考数学试题江苏省扬州市广陵区红桥高级中学2023-2024学年高一下学期3月月考数学试题江苏省盐城市五校联盟2023-2024学年高一下学期第一次学情调研检测(3月)数学试题甘肃省兰州新区贺阳高级中学2023-2024学年度高一下学期3月月考数学试题天津市和平区汇文中学2023-2024学年高一下学期第一次月考数学试题广东省深圳市桃源居中澳实验学校2023-2024学年高一下学期3月全国港澳台侨联考数学试卷天津市北辰区南仓中学2023-2024学年高一下学期3月教学质量过程性监测与诊断数学试题河北省邯郸市大名县第一中学2023-2024学年高一下学期3月月考数学试卷广东省江门市某校2023-2024学年高一下学期第一次质量检测数学试题江苏省常州市第二中学2023-2024学年高一下学期3月月考数学试卷福建省华安县第一中学2023-2024学年高一下学期第一次月考数学试卷重庆市杨家坪中学2023-2024学年高一下学期3月月考数学试卷四川省宜宾市珙县中学校2023-2024学年高一下学期3月月考数学试题河北省石家庄二中实验学校2023-2024学年高一下学期3月月考数学试题(已下线)2.5 从力的做功到向量的数量积6种常见考法归类(2)-【帮课堂】(北师大版2019必修第二册)黑龙江省哈尔滨市第一中学校2023-2024学年高一下学期第三次质量检测数学试题广东省茂名市电白区2023-2024学年高一下学期期中考试数学试题江苏省扬州市第一中学2023-204学年高一下学期3月月考数学试题广东省深圳市南山区为明学校2023-2024学年高一下学期3月月考数学试题湖南省邵阳市海谊中学2023-2024学年高一下学期3月月考数学试题(B卷)河北省保定市定州中学2024-2025学年高一上学期10月考试数学试题
名校
解题方法
2 . 如图,在 中,已知
中,已知 ,
,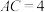 ,
,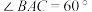 ,
, ,
, 分别为
分别为 ,
, 上的两点
上的两点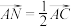 ,
,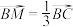 ,
, ,
, 相交于点
相交于点 .
.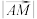 的值;
的值;
(2)求证: .
.
 中,已知
中,已知 ,
,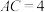 ,
,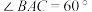 ,
, ,
, 分别为
分别为 ,
, 上的两点
上的两点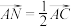 ,
,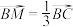 ,
, ,
, 相交于点
相交于点 .
.
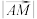 的值;
的值;(2)求证:
 .
.
您最近一年使用:0次
2024-03-06更新
|
3715次组卷
|
20卷引用:山东省青岛市即墨区第一中学2023-2024学年高一下学期第一次阶段检测数学试题
山东省青岛市即墨区第一中学2023-2024学年高一下学期第一次阶段检测数学试题浙江省临平萧山联考2023-2024学年高二上学期期末数学试题浙江省杭州市2023-2024学年高二上学期期末数学试题(已下线)6.4.1平面几何中的向量方法(已下线)模块一 专题3 平面向量的应用(A)河北省沧州市献县实验中学2023-2024学年高一下学期3月月考数学试题(已下线)第八章:向量的数量积与三角恒等变换(单元测试)-同步精品课堂(人教B版2019必修第三册)(已下线)高一下学期期中数学试卷(基础篇)-举一反三系列(已下线)专题3 平面向量的应用(期中研习室)福建省福州教育学院附属中学2023-2024学年高一下学期3月月考数学试卷河南省安阳市龙安高级中学2023-2024学年高一下学期3月月考数学试卷重庆市礼嘉中学2023-2024学年高一下学期第一次月考数学试题宁夏吴忠市青铜峡市宁朔中学2023-2024学年高一下学期3月月考数学试题河北省唐山市开滦第二中学2023-2024学年高一下学期4月月考数学试题浙江省杭州第七中学2023-2024学年高二上学期期末数学试题河北省石家庄二中实验学校2023-2024学年高一下学期3月月考数学试题(已下线)模块一专题3 《平面向量的应用》A基础卷(苏教版)(已下线)模块三 专题2 解答题分类练 专题5 三角函数与平面向量的实际应用(解答题)(北师大版高一期中)福建省龙岩市连城县第一中学2023-2024学年高一下学期5月月考数学试题(已下线)【高一模块二】类型1 以平面向量为背景的解答题(B卷提升卷)
名校
解题方法
3 . 在 中,内角
中,内角 所对的边分别是
所对的边分别是 ,已知
,已知 .
.
(1)求角 ;
;
(2)设边 的中点为
的中点为 ,若
,若 ,且
,且 的面积为
的面积为 ,求
,求 的长.
的长.
 中,内角
中,内角 所对的边分别是
所对的边分别是 ,已知
,已知 .
.(1)求角
 ;
;(2)设边
 的中点为
的中点为 ,若
,若 ,且
,且 的面积为
的面积为 ,求
,求 的长.
的长.
您最近一年使用:0次
2024-02-12更新
|
3014次组卷
|
7卷引用:山东省栖霞市第一中学2023-2024学年高一下学期3月月考数学试题
山东省栖霞市第一中学2023-2024学年高一下学期3月月考数学试题浙江省金丽衢十二校2023-2024学年高三上学期第一次联考数学试题(已下线)重难点3-2 解三角形的综合应用(8题型+满分技巧+限时检测)宁夏银川市第二中学2024届高三第一次模拟考试数学(理)试题(已下线)专题05 三角函数福建省三明市四校2023-2024学年高一下学期联考数学试题重庆市第七中学校2024-2025学年高二上学期第一次月考数学试卷
名校
解题方法
4 . 已知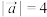 ,
, ,
, 与
与 的夹角为
的夹角为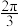 .
.
(1)求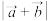 ;
;
(2)当 为何值时,
为何值时, ?
?
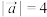 ,
, ,
, 与
与 的夹角为
的夹角为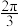 .
.(1)求
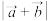 ;
;(2)当
 为何值时,
为何值时, ?
?
您最近一年使用:0次
2023-03-13更新
|
3051次组卷
|
36卷引用:山东省临沂市罗庄区2016-2017学年高一下学期期末考试数学(文)试题
山东省临沂市罗庄区2016-2017学年高一下学期期末考试数学(文)试题山东省青岛市胶州市第二中学2022-2023学年高一下学期3月月考数学试题2015-2016学年江西省上高二中高一5月月考理科数学试卷2015-2016学年江西省上高二中高一5月月考文科数学试卷内蒙古巴彦淖尔市第一中学2016-2017学年高一3月月考数学试题【全国百强校】海南省文昌中学2018-2019学年高一下学期段考数学试题四川省棠湖中学2019-2020学年高二上学期开学考试数学(理)试题四川省棠湖中学2019-2020学年高二上学期开学考试数学(文)试题安徽省淮南市寿县第一中学2020-2021学年高一下学期6月质量检测数学试题江苏省徐州市沛县2020-2021学年高一下学期第一次学情调研数学试题福建省三明市第一中学2020-2021学年高一下学期第一次月考数学试题河北省邯郸市大名县第一中学2020-2021学年高一下学期3月月考数学试题浙江省宁波市咸祥中学2021-2022学年高一下学期期中数学试题重庆市铁路中学校2021-2022学年高一下学期期中数学试题浙江省杭州市第四中学下沙校区2021-2022学年高一下学期期中数学试题安徽省淮北市第一中学2022-2023学年高一下学期第二次月考数学试题北京市朝阳区东北师范大学附属中学朝阳学校2022-2023学年高一下学期3月月考数学试题福建省三明第一中学2022-2023学年高一下学期期中考试数学试题北京市第一六六中学2022-2023学年高一下学期期中诊断数学试题第9章 平面向量(单元测试)-2022-2023学年高一数学同步精品课堂(苏教版2019必修第二册)福建省华安县第一中学2022-2023学年高一下学期第一次月考数学试题广东省清远市阳山县南阳中学2022-2023学年高一下学期第二次月考数学试题上海市浦东新区2022-2023学年高一下学期期末数学试题浙江省杭州市六县九校联考2022-2023学年高一下学期4月期中数学试题广东省深圳市人大附中深圳学校2022-2023学年高一下学期期中数学试题浙江省绍兴市越州中学2022-2023学年高一下学期期中数学试题河北省唐山市滦州市第六中学2022-2023学年高一下学期期中数学试题安徽省安庆市九一六学校2022-2023学年高一下学期第三次调研考试数学试题吉林省长春市新解放学校2022-2023学年高一下学期第一次月考数学试题福建省福州市鼓楼区福州黎明中学2022-2023学年高一下学期期中数学试题河南省焦作市第一中学2022-2023学年高一下学期3月月考数学试题福建省建瓯市芝华中学2023-2024学年高一下学期第一次阶段考试数学试题广东省江门市培英高级中学2023-2024学年高一下学期期中考试数学试题山西省阳泉市第一中学校2023-2024学年高一下学期5月期中考试数学试题(已下线)上海市高一下学期期末真题必刷03-期末考点大串讲(沪教版2020必修二)四川省南充市白塔中学2023-2024学年高一下学期第一次月考(3月)数学试题
名校
5 . 如图,在 中,
中, ,点
,点 在线段
在线段 上,且
上,且 .求:
.求: 的长;
的长;
(2)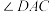 的大小.
的大小.
 中,
中, ,点
,点 在线段
在线段 上,且
上,且 .求:
.求:
 的长;
的长;(2)
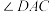 的大小.
的大小.
您最近一年使用:0次
2024-03-02更新
|
2287次组卷
|
22卷引用:山东省泰安市第三中学2022-2023学年高一下学期期中考试数学试题
山东省泰安市第三中学2022-2023学年高一下学期期中考试数学试题山东省菏泽市第一中学八一路校区2023-2024学年高一下学期3月月考数学试题人教A版(2019) 必修第二册 突围者(经验篇) 第6章 第4节平面向量的应用人教A版(2019) 必修第二册 必杀技 第6章 6.4.1 平面几何中的向量方法+6.4.2 向量在物理中的应用举例(已下线)6.4.1-6.4.2 向量在物理中的应用举例-2020-2021学年高一数学新教材配套学案(人教A版2019必修第二册)广东省深圳市南方科技大学附属中学2020-2021学年高一下学期期中数学试题苏教版(2019) 必修第二册 必杀技 第9章 平面向量 9.4 向量应用四川省绵阳市开元中学2021-2022年学年高一下学期期末适应性质量检测理科数学试题四川省绵阳市开元中学2021-2022年学年高一下学期期末适应性质量检测文科数学试题湖南省常德市临澧县第一中学2022-2023学年高一下学期3月第一次阶段性考试数学试题(已下线)6.4.1平面几何中的向量方法+6.4.2向量在物理中的应用举例 【第二练】“上好三节课,做好三套题“高中数学素养晋级之路(已下线)专题9.8平面向量-重难点突破及混淆易错规避(苏教版2019必修第二册)河南省郑州市中牟县第一高级中学2023-2024学年高一下学期3月月考数学试题(已下线)第八章:向量的数量积与三角恒等变换章末重点题型复习(1)-同步精品课堂(人教B版2019必修第三册)河北省邯郸市涉县第一中学2023-2024学年高一下学期3月月考数学试题广东省东莞市海德双语学校2023-2024学年高一下学期第一次月考数学试题安徽省安庆市怀宁县高河中学2023-2024学年高一下学期4月月考数学试题(已下线)期中考试押题卷-【帮课堂】(苏教版2019必修第二册)【典例题】 8.4.1向量的应用(1) 课堂例题-沪教版(2020)必修第二册第8章 平面向量陕西省兴平市南郊高级中学2023-2024学年高一下学期第一次质量检测数学试题【课后练】 1.7平面向量的应用举例 课后作业-湘教版(2019)必修(第二册)第1章 平面向量及其应用安徽省安庆市九一六学校2023-2024学年高一下学期期中考试数学试卷
名校
6 . (1)已知平面向量 、
、 ,其中
,其中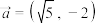 ,若
,若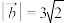 ,且
,且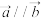 ,求向量
,求向量 的坐标表示;
的坐标表示;
(2)已知平面向量 、
、 满足
满足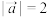 ,
,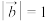 ,
, 与
与 的夹角为
的夹角为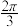 ,且(
,且( +
+
 )
) (
(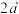
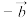 ),求
),求 的值.
的值.
 、
、 ,其中
,其中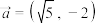 ,若
,若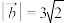 ,且
,且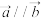 ,求向量
,求向量 的坐标表示;
的坐标表示;(2)已知平面向量
 、
、 满足
满足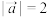 ,
,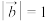 ,
, 与
与 的夹角为
的夹角为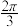 ,且(
,且( +
+
 )
) (
(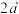
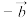 ),求
),求 的值.
的值.
您最近一年使用:0次
2021-02-28更新
|
6926次组卷
|
19卷引用:山东省青岛莱西市第一中学2021-2022学年高一下学期3月(网课)月考数学试题
山东省青岛莱西市第一中学2021-2022学年高一下学期3月(网课)月考数学试题山东省泰安第二中学2022-2023学年高一下学期3月月考数学试题山东省济宁市邹城市第一中学2023-2024学年高一下学期5月月考数学试题山东省菏泽市郓城县实验中学2023-2024学年高一下学期5月月考数学试题新疆乌苏市第一中学2020-2021学年高一下学期入学检测数学试题(已下线)第9章 平面向量(能力提升)-2020-2021学年高一数学单元测试定心卷(苏教版2019必修第二册)湖北省黄冈市蕲春县第一高级中学2020-2021学年高一下学期3月月考数学试题 安徽省池州市东至县第二中学2020-2021学年高一下学期3月月考数学试题湖北省黄冈市黄梅国际育才高级中学2020-2021学年高一下学期3月月考数学试题重庆市川维中学2020-2021学年高一下学期第一次月考数学试题江苏省南京市金陵中学2020-2021学年高一下学期6月阶段性考试数学试题湖北省黄冈市麻城市第二中学2020-2021学年高一下学期4月月考数学试题云南省昆明市第八中学2020-2021学年高一特色班下学期第一次月考数学试题重庆市南华中学校2021-2022学年高一下学期第一次调研数学试题河北省石家庄市第三十五中学2021-2022学年高一下学期4月月考数学试题吉林省白城市通榆县毓才高级中学2021-2022学年高一下学期第一次月考数学试题(已下线)专题强化训练一 平面向量的各类问题精选必刷题-2022-2023学年高一数学《考点·题型·技巧》精讲与精练高分突破系列(人教A版2019必修第二册)湖南省岳阳市平江县2022-2023学年高一下学期期末数学试题四川省成都西藏中学2023-2024学年高一上学期期中测试数学试卷
名校
解题方法
7 . 已知 ,
,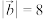 ,
, 与
与 的夹角为
的夹角为 .
.
(1)求 ;
;
(2)当 为何值时,
为何值时,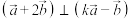 .
.
 ,
,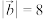 ,
, 与
与 的夹角为
的夹角为 .
.(1)求
 ;
;(2)当
 为何值时,
为何值时,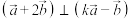 .
.
您最近一年使用:0次
2023-04-27更新
|
1736次组卷
|
8卷引用:山东省青岛第二中学2022-2023学年高一下学期期中数学试题
山东省青岛第二中学2022-2023学年高一下学期期中数学试题四川省成都市实验外国语学校2022-2023学年高一下学期期末数学试题(已下线)高一下学期期末考点大通关真题精选100题(1)-期中期末考点大串讲(已下线)专题7 大题分类练(向量的数量积与三角恒等变换)(基础夯实练)(人教B)黑龙江省哈尔滨市宾县第二中学2022-2023学年高一下学期第三次月考数学试卷甘肃省天水市第一中学2023-2024学年高二上学期开学考试数学试题甘肃省酒泉市实验中学2023-2024学年高一下学期期中考试数学试卷四川省泸州市龙马潭区2023-2024学年高一下学期6月期末考试数学试题
名校
解题方法
8 . 已知向量 ,
, 满足
满足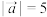 ,
, ,
, .
.
(1)求 与
与 的夹角的余弦值;
的夹角的余弦值;
(2)求 .
.
 ,
, 满足
满足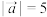 ,
, ,
, .
.(1)求
 与
与 的夹角的余弦值;
的夹角的余弦值;(2)求
 .
.
您最近一年使用:0次
2024-03-22更新
|
1584次组卷
|
8卷引用:山东省枣庄市滕州市2023-2024学年高一下学期期中质量检测数学试卷
名校
9 . 在 中,角
中,角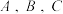 所对的边分别为
所对的边分别为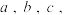 记
记 的面积为
的面积为 ,已知
,已知 .
.
(1)求角 的大小;
的大小;
(2)若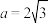 ,求
,求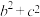 的最大值.
的最大值.
 中,角
中,角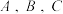 所对的边分别为
所对的边分别为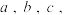 记
记 的面积为
的面积为 ,已知
,已知 .
.(1)求角
 的大小;
的大小;(2)若
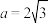 ,求
,求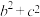 的最大值.
的最大值.
您最近一年使用:0次
2024-02-05更新
|
1745次组卷
|
8卷引用:山东省威海市2024届高三上学期期末数学试题
山东省威海市2024届高三上学期期末数学试题(已下线)考点17 解三角形中的最值问题 --2024届高考数学考点总动员【练】(已下线)艺体生新高考新结构全真模拟4(已下线)重难点3-2 解三角形的综合应用(8题型+满分技巧+限时检测)(已下线)专题1.11解三角形常考大题归类-重难点突破及混淆易错规避(人教A版2019必修第二册)湖南省长沙市南雅中学2023-2024学年高二下学期第一次月考数学试题(已下线)专题04解三角形的7种常考题型归类-《期末真题分类汇编》(北师大版(2019))陕西省西安市第八十五中学2023-2024学年高一下学期第一次月考数学试题
名校
解题方法
10 . 设向量 满足
满足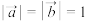 ,且
,且 .
.
(1)求 与
与 的夹角;
的夹角;
(2)求 的大小.
的大小.
 满足
满足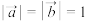 ,且
,且 .
.(1)求
 与
与 的夹角;
的夹角;(2)求
 的大小.
的大小.
您最近一年使用:0次
2021-10-14更新
|
5555次组卷
|
20卷引用:山东省郯城第一中学2021-2022学年高一下学期4月质量检测数学试题
山东省郯城第一中学2021-2022学年高一下学期4月质量检测数学试题2018-2019学年高中数学人教A版必修四第二章平面向量单元测试吉林省延边第二中学2018-2019学年高一下学期第二次月考数学试题辽宁省锦州市黑山县黑山中学2019-2020学年高一下学期线上教学检测数学试题福建省南平市2019-2020学年高一下学期期末考试数学试题河南省安阳市林州市2020-2021学年高一下学期期末数学试题海南省白沙黎族自治县白沙中学2020-2021学年高一下学期期中考试数学试题(已下线)第六章 平面向量及其应用综合测评(备作业)-【上好课】2020-2021学年高一数学同步备课系列(人教A版2019必修第二册)(已下线)第5课时 课后 向量的数量积重庆市实验中学2021-2022学年高一下学期第一次月考数学试题重庆市清华中学2021-2022学年高一下学期第一次月考数学试题广东省阳山县阳山中学2021-2022学年高一下学期教学质量检测3数学试题河南省实验中学2022-2023学年高一下学期第一次月考数学试题新疆喀什地区泽普县第二中学2022-2023学年高一下学期第一次月考数学试题山西省晋城市陵川县平城中学2022-2023学年高一下学期月考三数学试题河北省唐县第一中学2022-2023学年高一下学期5月月考数学试题新疆阿克苏市实验中学2022-2023学年高一下学期第三次月考数学试题(已下线)专题01 平面向量及其应用(1)-期末真题分类汇编(新高考专用)湖南省邵阳市第二中学2023-2024学年高一下学期6月期末考试数学试题江苏省徐州市睢宁县第一中学2023-2024学年高一下学期5月阶段检测数学试卷



