名校
解题方法
1 . 在分形艺术中会有下面的操作:将一长度为1的线段均分为三段,去掉中间一段,记为第1次操作:将剩下的线段分别又均分为三段,并各自去掉中间一段,记为第2次操作;……,每次操作都在上一次操作的基础上,将剩下的线段分别均分为三段,同样各自去掉中间的一段;操作过程不断进行下去.设第 次操作去掉的线段总长为
次操作去掉的线段总长为 ,若
,若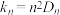 ,则数列
,则数列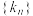 中取值最大的项为第
中取值最大的项为第_____ 项.
 次操作去掉的线段总长为
次操作去掉的线段总长为 ,若
,若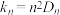 ,则数列
,则数列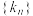 中取值最大的项为第
中取值最大的项为第
您最近一年使用:0次
名校
2 . 某汽车公司最新研发了一款新能源汽车,并在出厂前对100辆汽车进行了单次最大续航里程(理论上是指新能源汽车所装载的燃料或电池所能够提供给车行驶的最远里程)的测试.现对测试数据进行整理,得到如下的频率分布直方图: (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);
(2)由频率分布直方图计算得样本标准差s的近似值为49.75.根据大量的汽车测试数据,可以认为这款汽车的单次最大续航里程X近似地服从正态分布 ,其中μ近似为样本平均数
,其中μ近似为样本平均数 ,σ近似为样本标准差S.
,σ近似为样本标准差S.
(ⅰ)利用该正态分布,求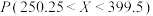 ;
;
(ⅱ)假设某企业从该汽车公司购买了20辆该款新能源汽车,记Z表示这20辆新能源汽车中单次最大续航里程位于区间(250.25,399.5)的车辆数,求E(Z);
参考数据:若随机变量ξ服从正态分布 ,则
,则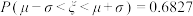 ,
,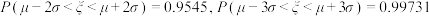 .
.
(3)某汽车销售公司为推广此款新能源汽车,现面向意向客户推出“玩游戏,送大奖”活动,客户可根据抛掷硬币的结果,操控微型遥控车在x轴上从原点O出发向右运动,已知硬币出现正、反面的概率都 ,客户每掷一次硬币,遥控车向右移动一次,若掷出正面,则遥控车向移动一个单位,若掷出反面,则遥控车向右移动两个单位,直到遥控车移到点(59,0)(胜利大本营)或点(60,0)(失败大本营)时,游戏结束,若遥控车最终停在“胜利大本营”,则可获得购车优惠券.设遥控车移到点
,客户每掷一次硬币,遥控车向右移动一次,若掷出正面,则遥控车向移动一个单位,若掷出反面,则遥控车向右移动两个单位,直到遥控车移到点(59,0)(胜利大本营)或点(60,0)(失败大本营)时,游戏结束,若遥控车最终停在“胜利大本营”,则可获得购车优惠券.设遥控车移到点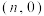 的概率为
的概率为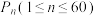 ,试证明数列
,试证明数列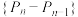 是等比数列
是等比数列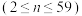 ,求出数列
,求出数列 的通项公式,并比较
的通项公式,并比较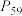 和
和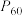 的大小.
的大小.
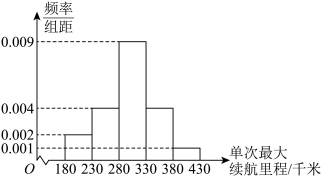
 (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);(2)由频率分布直方图计算得样本标准差s的近似值为49.75.根据大量的汽车测试数据,可以认为这款汽车的单次最大续航里程X近似地服从正态分布
 ,其中μ近似为样本平均数
,其中μ近似为样本平均数 ,σ近似为样本标准差S.
,σ近似为样本标准差S.(ⅰ)利用该正态分布,求
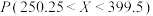 ;
;(ⅱ)假设某企业从该汽车公司购买了20辆该款新能源汽车,记Z表示这20辆新能源汽车中单次最大续航里程位于区间(250.25,399.5)的车辆数,求E(Z);
参考数据:若随机变量ξ服从正态分布
 ,则
,则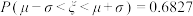 ,
,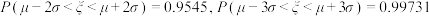 .
.(3)某汽车销售公司为推广此款新能源汽车,现面向意向客户推出“玩游戏,送大奖”活动,客户可根据抛掷硬币的结果,操控微型遥控车在x轴上从原点O出发向右运动,已知硬币出现正、反面的概率都
 ,客户每掷一次硬币,遥控车向右移动一次,若掷出正面,则遥控车向移动一个单位,若掷出反面,则遥控车向右移动两个单位,直到遥控车移到点(59,0)(胜利大本营)或点(60,0)(失败大本营)时,游戏结束,若遥控车最终停在“胜利大本营”,则可获得购车优惠券.设遥控车移到点
,客户每掷一次硬币,遥控车向右移动一次,若掷出正面,则遥控车向移动一个单位,若掷出反面,则遥控车向右移动两个单位,直到遥控车移到点(59,0)(胜利大本营)或点(60,0)(失败大本营)时,游戏结束,若遥控车最终停在“胜利大本营”,则可获得购车优惠券.设遥控车移到点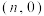 的概率为
的概率为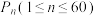 ,试证明数列
,试证明数列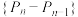 是等比数列
是等比数列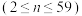 ,求出数列
,求出数列 的通项公式,并比较
的通项公式,并比较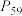 和
和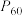 的大小.
的大小.
您最近一年使用:0次
2024-10-14更新
|
596次组卷
|
4卷引用:重庆市乌江新高考协作体2025届高三上学期高考质量调研(二)(10月)数学试题
重庆市乌江新高考协作体2025届高三上学期高考质量调研(二)(10月)数学试题山西省长治市2024-2025学年高三上学期9月质量监测数学试题(已下线)第五章 概率统计创新问题 专题二 概率统计与数列交汇 微点1 概率统计与数列交汇(一)【培优版】辽宁省三校2025届高三上学期10月联合教学质量检测数学试卷
3 . 已知数列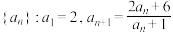 .
.
(1)证明: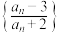 是等比数列;
是等比数列;
(2)已知数列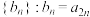 .
.
①求 的最大值;
的最大值;
②对任意的正整数 ,证明:
,证明: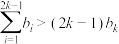 .
.
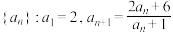 .
.(1)证明:
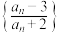 是等比数列;
是等比数列;(2)已知数列
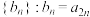 .
.①求
 的最大值;
的最大值;②对任意的正整数
 ,证明:
,证明: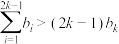 .
.
您最近一年使用:0次
名校
解题方法
4 . 已知数列 的前
的前 项和为
项和为 ,满足
,满足 ,数列
,数列 是等比数列,公比
是等比数列,公比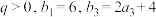 .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)设数列 满足
满足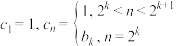 ,其中
,其中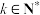 .
.
(i)求数列 的前2024项和;
的前2024项和;
(ii)求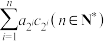 .
.
 的前
的前 项和为
项和为 ,满足
,满足 ,数列
,数列 是等比数列,公比
是等比数列,公比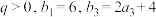 .
.(1)求数列
 和
和 的通项公式;
的通项公式;(2)设数列
 满足
满足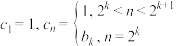 ,其中
,其中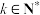 .
.(i)求数列
 的前2024项和;
的前2024项和;(ii)求
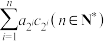 .
.
您最近一年使用:0次
2024-09-02更新
|
678次组卷
|
5卷引用:重庆市2025届高三上学期9月大联考数学试题
24-25高三上·江苏南通·开学考试
名校
5 . 若数列 为正项等比数列,
为正项等比数列,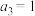 ,数列
,数列 为公差为6,首项为1的等差数列,则数列
为公差为6,首项为1的等差数列,则数列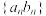 前5项和的最小值为( )
前5项和的最小值为( )
 为正项等比数列,
为正项等比数列,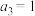 ,数列
,数列 为公差为6,首项为1的等差数列,则数列
为公差为6,首项为1的等差数列,则数列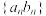 前5项和的最小值为( )
前5项和的最小值为( )A.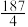 | B.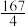 | C. | D.65 |
您最近一年使用:0次
名校
解题方法
6 . 从甲、乙、丙、丁4人中随机抽取3个人去做传球训练.训练规则是确定一人第一次将球传出,每次传球时,传球者都等可能地将球传给另外两个人中的任何一人,每次必须将球传出.
(1)记甲乙丙三人中被抽到的人数为随机变量 ,求
,求 的分布列;
的分布列;
(2)若刚好抽到甲乙丙三个人相互做传球训练,且第1次由甲将球传出,记 次传球后球在甲手中的概率为
次传球后球在甲手中的概率为 ,
,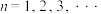 .
.
①直接写出 ,
, ,
, 的值;
的值;
②求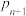 与
与 的关系式(
的关系式(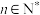 ),并求
),并求 (
(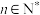 ).
).
(1)记甲乙丙三人中被抽到的人数为随机变量
 ,求
,求 的分布列;
的分布列;(2)若刚好抽到甲乙丙三个人相互做传球训练,且第1次由甲将球传出,记
 次传球后球在甲手中的概率为
次传球后球在甲手中的概率为 ,
,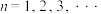 .
.①直接写出
 ,
, ,
, 的值;
的值;②求
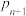 与
与 的关系式(
的关系式(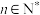 ),并求
),并求 (
(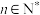 ).
).
您最近一年使用:0次
2024-04-29更新
|
1881次组卷
|
9卷引用:重庆市乌江新高考协作体2023-2024学年高二下学期5月期中考试数学试题
重庆市乌江新高考协作体2023-2024学年高二下学期5月期中考试数学试题江苏省盐城市五校联盟2023-2024学年高二下学期4月期中考试数学试题(已下线)专题07 概率与统计综合问题(6类题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(江苏专用)(已下线)专题03 第七章 随机变量及其分布列--高二期末考点大串讲(人教A版2019)(已下线)作业03 概率(1)-【暑假分层作业】(苏教版2019选择性必修第二册)内蒙古呼和浩特第二十一中2023-2024学年高二下学期期末考试数学试卷江苏省镇江市扬中市第二高级中学2024届高三下学期高考考前热身数学试题新疆石河子第一中学2023-2024学年高二下学期5月月考数学试题(已下线)周测21 随机变量及其分布列(高三一轮好卷复盘卷)
名校
7 . 已知数列 的前
的前 项和为
项和为 ,且满足
,且满足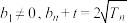 .
.
(1)证明: .
.
(2)当 时,求证:
时,求证: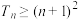 ;
;
(3)是否存在常数 ,使得
,使得 为等比数列?若存在,求出所有满足条件的
为等比数列?若存在,求出所有满足条件的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 的前
的前 项和为
项和为 ,且满足
,且满足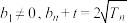 .
.(1)证明:
 .
.(2)当
 时,求证:
时,求证: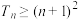 ;
;(3)是否存在常数
 ,使得
,使得 为等比数列?若存在,求出所有满足条件的
为等比数列?若存在,求出所有满足条件的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近一年使用:0次
2024-03-08更新
|
733次组卷
|
2卷引用:重庆市第八中学校2024届高三下学期高考适应性月考数学试卷 (五)
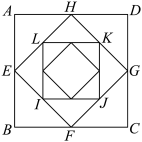
8 . 如图,正方形 的边长为1,连接
的边长为1,连接 各边的中点得到正方形
各边的中点得到正方形 ,连接正方形
,连接正方形 各边的中点得到正方形
各边的中点得到正方形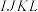 ,依此方法一直进行下去.记
,依此方法一直进行下去.记 为正方形
为正方形 的面积,
的面积, 为正方形
为正方形 的面积,
的面积, 为正方形
为正方形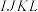 的面积,……..
的面积,……..  为
为 的前
的前 项和.给出下列四个结论:
项和.给出下列四个结论:
①存在常数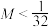 ,使得
,使得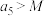 恒成立;②存在正整数
恒成立;②存在正整数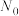 ,当
,当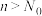 时,
时,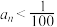 ;③存在常数
;③存在常数 ,使得
,使得 恒成立;④存在正整数
恒成立;④存在正整数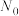 ,当
,当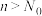 时,
时, 其中所有正确结论的序号是
其中所有正确结论的序号是_________ .
 的边长为1,连接
的边长为1,连接 各边的中点得到正方形
各边的中点得到正方形 ,连接正方形
,连接正方形 各边的中点得到正方形
各边的中点得到正方形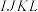 ,依此方法一直进行下去.记
,依此方法一直进行下去.记 为正方形
为正方形 的面积,
的面积, 为正方形
为正方形 的面积,
的面积, 为正方形
为正方形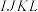 的面积,……..
的面积,……..  为
为 的前
的前 项和.给出下列四个结论:
项和.给出下列四个结论:
①存在常数
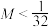 ,使得
,使得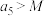 恒成立;②存在正整数
恒成立;②存在正整数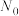 ,当
,当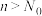 时,
时,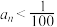 ;③存在常数
;③存在常数 ,使得
,使得 恒成立;④存在正整数
恒成立;④存在正整数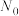 ,当
,当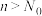 时,
时, 其中所有正确结论的序号是
其中所有正确结论的序号是
您最近一年使用:0次
2024-01-19更新
|
343次组卷
|
3卷引用:重庆市万州二中教育集团2023-2024学年高二下学期入学质量监测数学试题
重庆市万州二中教育集团2023-2024学年高二下学期入学质量监测数学试题北京市东城区2023-2024学年高二上学期期末统一检测数学试卷(已下线)第4章 数列 单元综合检测(难点)-2023-2024学年高二数学同步精品课堂(沪教版2020选择性必修第一册)
名校
解题方法
9 . 某区域市场中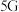 智能终端产品的制造全部由甲、乙两公司提供技术支持.据市场调研及预测,
智能终端产品的制造全部由甲、乙两公司提供技术支持.据市场调研及预测,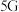 商用初期,该区域市场中采用的甲公司与乙公司技术的智能终端产品各占一半,假设两家公司的技术更新周期一致,且随着技术优势的体现,每次技术更新后,上一周期采用乙公司技术的产品中有
商用初期,该区域市场中采用的甲公司与乙公司技术的智能终端产品各占一半,假设两家公司的技术更新周期一致,且随着技术优势的体现,每次技术更新后,上一周期采用乙公司技术的产品中有 转而采用甲公司技术,采用甲公司技术的产品中有
转而采用甲公司技术,采用甲公司技术的产品中有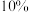 转而采用乙公司技术.设第
转而采用乙公司技术.设第 次技术更新后,该区域市场中采用甲公司与乙公司技术的智能终端产品占比分别为
次技术更新后,该区域市场中采用甲公司与乙公司技术的智能终端产品占比分别为 和
和 ,不考虑其他因素的影响.
,不考虑其他因素的影响.
(1)用 表示
表示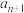 ,并求使数列
,并求使数列 是等比数列的实数
是等比数列的实数 .
.
(2)经过若干次技术更新后,该区域市场采用甲公司技术的智能终端产品的占比能否达到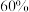 以上?若能,则至少需要经过几次技术更新;若不能,请说明理由.
以上?若能,则至少需要经过几次技术更新;若不能,请说明理由.
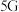 智能终端产品的制造全部由甲、乙两公司提供技术支持.据市场调研及预测,
智能终端产品的制造全部由甲、乙两公司提供技术支持.据市场调研及预测,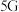 商用初期,该区域市场中采用的甲公司与乙公司技术的智能终端产品各占一半,假设两家公司的技术更新周期一致,且随着技术优势的体现,每次技术更新后,上一周期采用乙公司技术的产品中有
商用初期,该区域市场中采用的甲公司与乙公司技术的智能终端产品各占一半,假设两家公司的技术更新周期一致,且随着技术优势的体现,每次技术更新后,上一周期采用乙公司技术的产品中有 转而采用甲公司技术,采用甲公司技术的产品中有
转而采用甲公司技术,采用甲公司技术的产品中有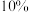 转而采用乙公司技术.设第
转而采用乙公司技术.设第 次技术更新后,该区域市场中采用甲公司与乙公司技术的智能终端产品占比分别为
次技术更新后,该区域市场中采用甲公司与乙公司技术的智能终端产品占比分别为 和
和 ,不考虑其他因素的影响.
,不考虑其他因素的影响.(1)用
 表示
表示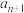 ,并求使数列
,并求使数列 是等比数列的实数
是等比数列的实数 .
.(2)经过若干次技术更新后,该区域市场采用甲公司技术的智能终端产品的占比能否达到
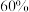 以上?若能,则至少需要经过几次技术更新;若不能,请说明理由.
以上?若能,则至少需要经过几次技术更新;若不能,请说明理由.
您最近一年使用:0次
2024-01-03更新
|
726次组卷
|
6卷引用:重庆市乌江新高考协作体2024届高三上学期高考第一次联合调研抽测数学试题
重庆市乌江新高考协作体2024届高三上学期高考第一次联合调研抽测数学试题甘肃省白银市靖远县第四中学2023-2024学年高二上学期1月期末考试数学模拟试题(已下线)考点8 等差、等比数列的实际应用 2024届高考数学考点总动员(已下线)考点11 由实际问题探究递推关系 2024届高考数学考点总动员(已下线)1.3.1 等比数列7种常见考法归类(3)(已下线)第04讲 数列的通项公式(十八大题型)(练习)-2
2023·全国·模拟预测
名校
解题方法
10 . 已知 为数列
为数列 的前
的前 项和,
项和,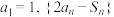 是公差为1的等差数列.
是公差为1的等差数列.
(1)证明:数列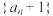 是等比数列,并求
是等比数列,并求 的通项公式;
的通项公式;
(2)若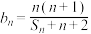 ,数列
,数列 的最大项为
的最大项为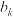 ,求
,求 的值.
的值.
 为数列
为数列 的前
的前 项和,
项和,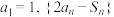 是公差为1的等差数列.
是公差为1的等差数列.(1)证明:数列
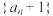 是等比数列,并求
是等比数列,并求 的通项公式;
的通项公式;(2)若
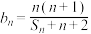 ,数列
,数列 的最大项为
的最大项为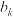 ,求
,求 的值.
的值.
您最近一年使用:0次



