名校
1 . 已知 是等比数列
是等比数列 的前
的前 项和,且
项和,且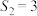 ,
,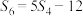 ,则
,则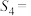 ( )
( )
 是等比数列
是等比数列 的前
的前 项和,且
项和,且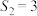 ,
,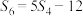 ,则
,则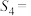 ( )
( )| A.11 | B.13 | C.15 | D.17 |
您最近一年使用:0次
2023-11-13更新
|
1716次组卷
|
12卷引用:浙江省衢州、丽水、湖州三地市2024届高三上学期11月教学质量检测数学试题
浙江省衢州、丽水、湖州三地市2024届高三上学期11月教学质量检测数学试题(已下线)专题05 数列(已下线)考点6 等比数列的前n项和的性质 2024届高考数学考点总动员【练】(已下线)专题6.2 等比数列及其前n项和【十大题型】浙江省温州市平阳县万全综合高级中学2023-2024学年中职高二下学期期末普高数学试题江苏省张家港市暨阳高级中学2023-2024学年高二上学期12月自主学习能力测试数学试卷(已下线)第4章:数列章末重点题型复习-【题型分类归纳】2023-2024学年高二数学同步讲与练(苏教版2019选择性必修第一册)(已下线)专题25 等比数列片段和的性质及等比数列的奇数项与偶数项和(期末选择题25)-2023-2024学年高二数学上学期期末题型秒杀技巧及专项练习(人教A版2019)(已下线)4.2 等比数列(第2课时)(六大题型)(分层练习)-2023-2024学年高二数学同步精品课堂(沪教版2020选择性必修第一册)(已下线)专题04 等比数列(十六大题型+过关检测专训)(2)江西省南昌市第十九中学2023-2024学年高二下学期3月月考数学试题(已下线)第四章:数列章末重点题型复习-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第二册)
名校
2 . 等差数列 的公差为2,前n项和为
的公差为2,前n项和为 ,若p:
,若p: ,
, ,
, 成等比数列,q:
成等比数列,q: 的首项为0,则( )
的首项为0,则( )
 的公差为2,前n项和为
的公差为2,前n项和为 ,若p:
,若p: ,
, ,
, 成等比数列,q:
成等比数列,q: 的首项为0,则( )
的首项为0,则( )| A.p是q的充要条件 | B.p是q的既不充分也不必要条件 |
| C.p是q的充分不必要条件 | D.p是q的必要不充分条件 |
您最近一年使用:0次
2022-05-03更新
|
900次组卷
|
6卷引用:浙江省金华十校2023-2024学年高三上学期11月模拟考试预演数学试题
2022·浙江·模拟预测
名校
解题方法
3 . 设 为等比数列,设
为等比数列,设 和
和 分别为
分别为 的前n项和与前n项积,则下列选项错误的是( )
的前n项和与前n项积,则下列选项错误的是( )
 为等比数列,设
为等比数列,设 和
和 分别为
分别为 的前n项和与前n项积,则下列选项错误的是( )
的前n项和与前n项积,则下列选项错误的是( )A.若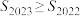 ,则 ,则 不一定是递增数列 不一定是递增数列 | B.若 ,则 ,则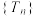 不一定是递增数列 不一定是递增数列 |
C.若 为递增数列,则可能存在 为递增数列,则可能存在 | D.若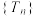 是递增数列,则 是递增数列,则 一定成立 一定成立 |
您最近一年使用:0次
真题
名校
4 . 记 为等比数列
为等比数列 的前n项和.若
的前n项和.若 ,
, ,则
,则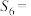 ( )
( )
 为等比数列
为等比数列 的前n项和.若
的前n项和.若 ,
, ,则
,则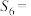 ( )
( )| A.7 | B.8 | C.9 | D.10 |
您最近一年使用:0次
2021-06-07更新
|
40465次组卷
|
109卷引用:考点21 等比数列及其前n项和-备战2022年高考数学一轮复习考点帮(浙江专用)
(已下线)考点21 等比数列及其前n项和-备战2022年高考数学一轮复习考点帮(浙江专用)2021年全国高考甲卷数学(文)试题(已下线)考点02 等比数列-2022年高考数学(文)一轮复习小题多维练(全国通用)(已下线)考点13 等比数列及其前n项和-备战2022年高考数学(文)一轮复习考点微专题(已下线)考点22 等比数列及其前n项和-备战2022年高考数学(文)一轮复习考点帮(已下线)专题07 数列及其应用-十年(2012-2021)高考数学真题分项汇编(全国通用)(已下线)专题08 数列-2021年高考真题和模拟题数学(文)分项汇编(全国通用)(已下线)6.2 等比数列(精讲)-【一隅三反】2022年高考数学一轮复习(新高考地区专用)(已下线)考向15 等比数列-备战2022年高考数学一轮复习考点微专题(上海专用)(已下线)专题7.3 等比数列及其前n项和(练)- 2022年高考数学一轮复习讲练测(新教材新高考)(已下线)专题18等比数列-2022年高三毕业班数学常考点归纳与变式演练(文理通用)(已下线)专题08 数列-五年(2017-2021)高考数学真题分项汇编(文科+理科)(已下线)考点09 数列-备战2022年高考数学学霸纠错 (新高考专用)(已下线)专题04数列求和及综合应用之讲案(文科)第一篇 热点、难点突破篇-《2022年高考文科数学二轮复习讲练测》(全国课标版)(已下线)专题04数列求和及综合应用之练案(文科)第一篇 热点、难点突破篇-《2022年高考文科数学二轮复习讲练测》(全国课标版)(已下线)专题03等差数列等比数列之练案(文科)第一篇 热点、难点突破篇-《2022年高考文科数学二轮复习讲练测》(全国课标版)(已下线)第1讲 等差数列与等比数列(讲·)-2022年高考数学二轮复习讲练测(新教材地区专用)(已下线)专题03等差数列等比数列之讲案(文科)第一篇 热点、难点突破篇-《2022年高考文科数学二轮复习讲练测》(全国课标版)(已下线)热点03 等差数列与等比数列-2022年高考数学【热点·重点·难点】专练(全国通用)(已下线)专题04数列求和及综合应用 讲案 (理科)第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测》(全国课标版)河南省新乡市原阳县第一高级中学2021-2022学年高三上学期12月月考数学(理)试题河南省新乡市原阳县第一高级中学2021-2022学年高三上学期12月月考数学(文)试题(已下线)专题07 数列小题大做-备战2022年高考数学冲刺横向强化精练精讲(已下线)专题08 数列小题大做-备战2022年高考数学冲刺横向强化精练精讲(新高考专用)(已下线)押新高考第14题 数列-备战2022年高考数学临考题号押题(新高考专用)(已下线)查补易混易错点09 数列-【查漏补缺】2022年高考数学(文)三轮冲刺过关(已下线)查补易混易错点04 数列-【查漏补缺】2022年高考数学三轮冲刺过关(新高考专用)(已下线)押全国卷(文科)第4,9题 数列-备战2022年高考数学(文)临考题号押题(全国卷)(已下线)2022年高考考前20天终极冲刺攻略(三)【数学】(新高考地区专用) (5月30日)江西省新余市第一中学2022届高三5月全真模拟考试数学(理)试题(已下线)第5讲 数列与不等式(已下线)专题21 等比数列-2023届高考数学一轮复习精讲精练(新高考专用)(已下线)数学-2022年高考押题预测卷01(北京卷)(已下线)专题06 数列选填题(已下线)第41讲 等比数列(已下线)考点6-2 等比数列(文理)(已下线)专题06 数列(文理)(已下线)第40讲 数列的概念与等差数列(已下线)第03讲 等比数列及前n项和(练)(已下线)考向20等比数列及其前n项和(重点)-1宁夏石嘴山市平罗中学2023届高三(重点班)上学期期中考试数学(文)试题宁夏银川市第二中学2023届高三上学期统练三数学(理)试题宁夏回族自治区银川市第六中学2022-2023学年高三上学期11月月考数学试题(已下线)专题5 数列 第1讲 等差数列、等比数列广西梧州市藤县第六中学2023届高三上学期热身考试数学(文)试题(已下线)专题16 等比数列-3(已下线)专题14 数列(2)(已下线)拓展五:近五年数列高考真题分类汇编(1)全国甲乙卷3年真题分类汇编《数列》选填题全国甲乙卷5年真题分类汇编《数列》选填题(已下线)专题7 等比数列的性质 微点2 等比数列前n项和的性质青海省玉树藏族自治州第二民族高级中学2023届高三第七次模拟理科数学试题(已下线)专题08 数列广东省惠州市惠东县2023届高三上学期第二次教学质量检测数学试题广西壮族自治区桂林市第十七中学2023届高三上学期11月月考数学试题(已下线)第03讲 等比数列及其前n项和(练习)(已下线)考点6 等比数列的前n项和的性质 2024届高考数学考点总动员(已下线)艺体生一轮复习 第六章 数列 第26讲 等差数列【练】(已下线)艺体生一轮复习 第六章 数列 第27讲 等比数列【讲】1号卷·A10联盟2022届全国高考第一轮总复习试卷数学(理科)试题(十一)(已下线)专题04 数列及求和(分层练)(四大题型+14道精选真题)(已下线)专题30 等比数列通项与前n项和江苏省扬州中学、盐城中学、淮阴中学、丹阳中学四校2023-2024学年高三下学期调研测试联考数学试卷(已下线)专题05 数列小题(7类题型,文科)专题18数列选择填空题(已下线)五年全国文科专题08数列选择填空题四川省成都市天府新区太平中学2024届高三数学文科模拟测试(三)(已下线)第03讲 等比数列及其前n项和(九大题型)(讲义)-2海南省儋州市鑫源高级中学2022-2023学年高三上学期10月检测数学试题(已下线)专题04 等比数列小题检测-2020-2021学年高二数学数列专题复习课(人教A版2019选择性必修第二册)广西平果市第二中学2020-2021学年高一下学期期中考试数学试题人教A版(2019) 选修第二册 突围者 第四章 章末培优专练北师大版(2019) 选修第二册 名师精选 第三单元 等比数列 A卷北师大版(2019) 选修第二册 突围者 第一章 数列 章末培优专练(已下线)专题10 《数列》中的高考真题训练)-2021-2022学年高二数学同步培优训练系列(苏教版2019选择性必修第一册)人教B版(2019) 选修第三册 名师精选 第三单元 等比数列 A卷人教B版(2019) 选修第三册 必杀技 第五章 素养检测安徽省亳州市第一中学2021-2022学年高二下学期3月月考数学试题(已下线)专题1.2 数列 章末检测2(中)-【满分计划】2021-2022学年高二数学阶段性复习测试卷(人教A版2019选择性必修第二册)(已下线)卷04 等比数列 A卷 ·基础达标 -【重难点突破】2021-2022学年高二数学名校好题汇编同步测试卷(人教A版选择性必修第二册)吉林省长春市实验中学2021-2022学年高二下学期4月月考数学试题湘教版(2019) 选修第一册 突围者 第1章 章末培优专练湘教版(2019) 选修第一册 突围者 第1章 章末培优专练2023版 苏教版(2019) 选修第一册 突围者 第4章 章末培优专练2023版 湘教版(2019) 选修第一册 过关斩将 第1章 综合拔高练陕西省延安市第一中学2022-2023学年高二上学期第一次月考文科数学试题陕西省咸阳市高新一中2022-2023学年高二上学期期中理科数学试题(B卷)陕西省咸阳市兴平市南郊高级中学2022-2023学年高二上学期第一次质量检测理科数学试题陕西省兴平市南郊高级中学2022-2023学年高二上学期第一次质量检测文科数学试题河北省邢台市第一中学2022-2023学年高二上学期第三次月考数学试题吉林省长春市第七中学2022-2023学年高二上学期期中数学试题吉林省长春市第二实验中学2022-2023学年高二上学期期末数学试题河南省新乡市河南师大附中实验学校2021-2022学年高二上学期10月月考数学试题陕西省汉中市2022-2023学年高二上学期期末理科数学试题湖北省十堰市丹江口市第二中学2022-2023学年高二下学期5月月考数学试题甘肃省兰州市第一中学2023-2024学年高二上学期10月月考数学试题福建省漳州市华安县第一中学2023-2024学年高二上学期第一次(10月)月考数学试题4.3.2 等比数列的前n项和公式练习黑龙江省大兴安岭地区呼玛县高级中学2021-2022学年高二上学期期末数学试题人教A版(2019) 选修第二册 数学奇书 第四章 数列 4.3等比数列 4.3.2等比数列的前n项和公式 第1课时 等比数列的前n项和陕西省咸阳市实验中学2022-2023学年高二上学期第二次月考数学试题专题03等比数列(已下线)重难点03:数列近3年高考真题赏析-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第二册)(已下线)1.3.2等比数列的前n项和(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第二册)山东省淄博市第七中学2023-2024学年高二下学期3月月考数学试题山东省淄博市临淄中学2023-2024学年高二下学期4月阶段检测数学试题北京市第八中学2023-2024学年高二下学期期中练习数学试题北京市第六十六中学2023-2024学年高二下学期6月月考质量检测数学试题广东省广东实验中学越秀学校2023-2024学年高二下学期5月段考数学试卷
11-12高三下·江西·开学考试
名校
解题方法
5 . 设等比数列 的前
的前 项和为
项和为 ,若
,若 ,则
,则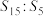 等于( )
等于( )
 的前
的前 项和为
项和为 ,若
,若 ,则
,则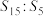 等于( )
等于( )A.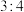 | B.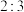 | C. | D. |
您最近一年使用:0次
2023-11-03更新
|
1967次组卷
|
45卷引用:浙江省湖州市湖州中学2024届高三上学期第一次质量检测数学试题
浙江省湖州市湖州中学2024届高三上学期第一次质量检测数学试题(已下线)2012届江西省师大附中高三下学期开学考试理科数学(已下线)考点02 等比数列-2022年高考数学(文)一轮复习小题多维练(全国通用)(已下线)6.2 等比数列(精练)-【一隅三反】2022年高考数学一轮复习(新高考地区专用)(已下线)2012-2013学年辽宁省丹东市宽甸二中高二下学期期初摸底理科数学卷(已下线)2012-2013学年四川成都六校协作体高一下学期期中考试数学试卷广东省惠州市崇雅实验学校2017-2018学年高二单元训练(数列)数学试题【全国百强校】安徽省蚌埠第二中学2018-2019学年高一下学期第一次月考数学试题广东省汕头市金山中学2018-2019学年高一下学期第一次月考数学试题重庆市育才中学2014-2015学年高一下学期期中数学(文)试题甘肃省甘南藏族自治州合作第一中学2019-2020学年高二上学期期中数学试题广东省佛山市第一中学2019-2020学年高一下学期第一次段考数学试题四川省成都市第十七中学2019-2020学年高一下学期期中数学试题湖北省荆州中学2020-2021学年高二上学期期末数学试题(已下线)专题06 第一章 复习与检测 核心素养练习 -【新教材精创】2020-2021学年高二数学新教材知识讲学(人教A版选择性必修第二册)贵州省贵阳市清镇养正学校2018-2019学年高一下学期期中考试数学试题福建省泉州第五中学2020-2021学年高二下学期入学考试数学试题(已下线)【新教材精创】5.3.2等比数列的前n项和 导学案(已下线)第四章 数列(能力测评卷)-2020-2021学年高二数学单元复习(人教A版2019选择性必修第二册)(已下线)第四章 数列(章末复习)-2020-2021学年高二数学单元复习(人教A版2019选择性必修第二册)辽宁省阜蒙县蒙古族高级中学2020-2021学年高二4月第二次月考数学试题北师大版(2019) 选修第二册 突围者 第一章 第三节 等比数列 课时2 等比数列的前n项和人教B版(2019) 选修第三册 必杀技 第五章 5.3.2 课时2 等比数列的前n项和(2)河南省周口市扶沟县第二高级中学2021-2022学年高二上学期第一次摸底考试数学试题河南省周口市扶沟县第二高级中学2021-2022学年高二第一次摸底数学试题四川省成都外国语学校2021-2022学年高一下学期期中考试数学(理)试题四川省成都外国语学校2021-2022学年高一下学期期中考试数学(文)试题广东省佛山市南海区南海中学2021-2022学年高二下学期第一次大测数学试题湘教版(2019) 选修第一册 突围者 第1章 第三节 课时2 等比数列的前n项和(已下线)4.3.3 等比数列的前n项和-2022-2023学年高二数学《基础·重点·难点 》全面题型高分突破(苏教版2019选择性必修第一册)湖北省襄阳市南漳县第一中学2021-2022学年高二下学期3月月考数学试题(已下线)4.3.2.1 等比数列的前n项和(练习)新疆兵团第三师图木舒克市鸿德实验学校2022-2023学年高二下学期第一次月考数学试题(已下线)期末测试卷01(培优卷)-【满分计划】2022-2023学年高二数学阶段性复习测试卷(苏教版2019选择性必修第一册)吉林省四平市四平盲童学校2021-2022学年高一上学期期末数学试题甘肃省兰州市兰州第一中学2023-2024学年高二上学期期中数学试题(已下线)模块一 专题5 等差数列与等比数列 期末终极研习室(2023-2024学年第一学期)高二人教A版(已下线)专题25 等比数列片段和的性质及等比数列的奇数项与偶数项和(期末选择题25)-2023-2024学年高二数学上学期期末题型秒杀技巧及专项练习(人教A版2019)(已下线)专题04 等比数列(十六大题型+过关检测专训)(3)(已下线)4.3.2 等比数列的前n项和公式(6大题型)精练-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第二册) (已下线)第四章:数列章末重点题型复习-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第二册)(已下线)模块一 专题1 数列基础、等差数列和等比数列【讲】高二下人教B版(已下线)模块一 专题2 数列基础、等差数列和等比数列【讲】高二下北师大版【课后练】 第1.3节综合训练 课后作业-湘教版(2019)选择性必修第一册 第1章 数列【随堂练】1.3.3.2 等比数列前n项和的性质及应用 随堂练习-湘教版(2019)选择性必修第一册 第1章 数列
6 . 已知数列 满足
满足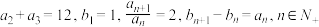
(1)求数列 的通项公式;
的通项公式;
(2)求证: .
.
 满足
满足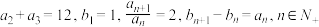
(1)求数列
 的通项公式;
的通项公式;(2)求证:
 .
.
您最近一年使用:0次
2020-11-29更新
|
891次组卷
|
3卷引用:浙江省9+1高中联盟2020-2021学年高三上学期期中数学试题
浙江省9+1高中联盟2020-2021学年高三上学期期中数学试题浙江省温州市苍南县金乡卫城中学2020-2021学年高二下学期第一次月考数学试题(已下线)期末模块检测(提升卷)-2020-2021学年高二数学新教材单元双测卷(人教A版2019选择性必修第二册)
真题
名校
7 . 设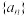 是等比数列,且
是等比数列,且 ,
, ,则
,则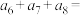 ( )
( )
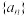 是等比数列,且
是等比数列,且 ,
, ,则
,则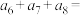 ( )
( )| A.12 | B.24 | C.30 | D.32 |
您最近一年使用:0次
2020-07-08更新
|
43927次组卷
|
145卷引用:考点21 等比数列及其前n项和-备战2022年高考数学一轮复习考点帮(浙江专用)
(已下线)考点21 等比数列及其前n项和-备战2022年高考数学一轮复习考点帮(浙江专用)2020年全国统一高考数学试卷(文科)(新课标Ⅰ)专题05+数列-2021高考数学(理)高频考点、热点题型归类强化(已下线)专题08 数列——2020年高考真题和模拟题文科数学分项汇编(已下线)专题12 数列——三年(2018-2020)高考真题文科数学分项汇编(已下线)专题08 数列-五年(2016-2020)高考数学(文)真题分项(已下线)专题18 等差数列与等比数列-十年(2011-2020)高考真题数学分项河南省开封市立洋外国语学校2020-2021学年高三第一次月考数学试题(已下线)考点20 等差数列与等比数列-2021年新高考数学一轮复习考点扫描(已下线)第13练 等比数列与求和-2021年高考数学一轮复习小题必刷(山东专用)(已下线)考点21 等差数列及其前n项和-备战2021年高考数学(文)一轮复习考点一遍过(已下线)考点22 等比数列及其前n项和-备战2021年高考数学(文)一轮复习考点一遍过(已下线)专题7.3 等比数列及其前n项和(练)-2021年新高考数学一轮复习讲练测(已下线)专题7.3 等比数列及其前n项和(精讲)-2021年新高考数学一轮复习学与练河南省南阳市华龙高级中学2020-2021学年上学期高三第二次月考文科数学试题陕西省咸阳市高新一中2020-2021学年高三上学期期中质量检测文科数学试题(已下线)第22练 等比数列-2021年高考数学(文)一轮复习小题必刷西藏拉萨那曲第二高级中学2021届高三第一次月考数学(理)试题西藏拉萨那曲第二高级中学2021届高三第一次月考数学(文)试题(已下线)热点08 数列与不等式-2021年高考数学【热点·重点·难点】专练(新高考)(已下线)热点07 数列与不等式-2021年高考数学(文)【热点·重点·难点】专练(已下线)专题07 数列(讲)-2021年高考数学二轮复习讲练测(新高考版)(已下线)专题07 数列(讲)-2021年高考数学二轮复习讲练测(文理通用)(已下线)专题07 数列应用-备战2021年高考数学(文)经典小题考前必刷集合(已下线)专题06 数列-备战2021年高考数学(文)纠错笔记甘肃省金昌市第一中学2021届高三一模数学(文)试题西藏自治区林芝市第二高级中学2021届高三上学期第二次月考数学(文)试题(已下线)解密10 等差数列、等比数列(分层训练)-【高频考点解密】2021年高考数学(文)二轮复习讲义+分层训练(已下线)专题7.3 等比数列及其前n项和(讲)- 2022年高考数学一轮复习讲练测(新教材新高考)(已下线)考点37 等比数列-备战2021年高考数学经典小题考前必刷(新高考地区专用)陕西省西安市庆华中学2020-2021学年高三上学期第二次月考文科数学试题河北省石家庄市第二中学2022届高三上学期开学考试数学试题(已下线)专题29等比数列通项与前n项和-2022年(新高考)数学高频考点+重点题型陕西省汉中市2021-2022学年高三上学期第一次校际联考理科数学试题(已下线)考点02 等比数列-2022年高考数学(文)一轮复习小题多维练(全国通用)(已下线)第28讲 等比数列及其前n项和(讲)- 2022年高考数学一轮复习讲练测(课标全国版)(已下线)考点13 等比数列及其前n项和-备战2022年高考数学(文)一轮复习考点微专题(已下线)考点22 等比数列及其前n项和-备战2022年高考数学(文)一轮复习考点帮(已下线)“8+4+4”小题强化训练(30)等比数列及其前n项和-2022届高考数学一轮复习(江苏等新高考地区专用)(已下线)考向28 等比数列及其前n项和(重点)-备战2022年高考数学一轮复习考点微专题(新高考地区专用)(已下线)专题07 数列及其应用-十年(2012-2021)高考数学真题分项汇编(全国通用)人教B版(2019) 选修第三册 突围者 第五章 高考挑战(已下线)专题18等比数列-2022年高三毕业班数学常考点归纳与变式演练(文理通用)江苏省南京市中华中学2021-2022学年高三上学期12月月考数学试题(已下线)第1讲 等差数列与等比数列(讲·)-2022年高考数学二轮复习讲练测(新教材地区专用)(已下线)专题03等差数列等比数列之讲案(文科)第一篇 热点、难点突破篇-《2022年高考文科数学二轮复习讲练测》(全国课标版)(已下线)专题09 数列(选择题、填空题)-备战2022年高考数学(文)母题题源解密(全国甲卷)(已下线)专题03等差数列等比数列之讲案(理科)第一篇 热点、难点突破篇-《2022年高考理科数学二轮复习讲练测》(全国课标版)(已下线)专题11 有关等差(比)数列的基本运算——备战2022年高考数学二轮复习常考点专题突破(已下线)专题22 等差等比数列性质的巧用-学会解题之高三数学万能解题模板【2022版】河南省新乡市原阳县第一高级中学2021-2022学年高三上学期12月月考数学(理)试题河南省新乡市原阳县第一高级中学2021-2022学年高三上学期12月月考数学(文)试题人教B版(2019) 选修第三册 一蹴而就 第五章 高考真题(已下线)类型二 等比数列-【题型突破】备战2022年高考数学二轮基础题型+重难题型突破(新高考专用)(已下线)专题35文科数学高考真题重组模拟测试(三)-备战2022年高考数学冲刺横向强化精练精讲(已下线)查补易混易错点09 数列-【查漏补缺】2022年高考数学(文)三轮冲刺过关(已下线)押全国卷(文科)第4,9题 数列-备战2022年高考数学(文)临考题号押题(全国卷)宁夏银川一中2022届高三下学期考前热身训练数学(文)试题(已下线)2022年高考考前最后一课-数学(正式版)-【考前预测篇2】命题专家押题(已下线)4.2 等比数列(精练)-【一隅三反】2023年高考数学一轮复习(基础版)(新高考地区专用)(已下线)专题21 等比数列-2023届高考数学一轮复习精讲精练(新高考专用)(已下线)专题06 数列选填题(已下线)第41讲 等比数列(已下线)专题07 数列(测)(已下线)考向20等比数列及其前n项和(重点) - 3四川省内江市威远中学校2022-2023学年高三上学期第三次月考数学(文)试题(已下线)模块三 专题5 数列(已下线)专题16 等比数列-3(已下线)重组卷01(文科)(已下线)拓展五:近五年数列高考真题分类汇编(1)全国甲乙卷5年真题分类汇编《数列》选填题(已下线)专题7 等比数列的性质 微点2 等比数列前n项和的性质广东省罗定中学城东学校2023届高三上学期9月调研数学试题(已下线)第三节 等比数列 (讲)江苏省南京市六校联合体2023-2024学年高三上学期10月联合调研数学试题内蒙古赤峰市赤峰二中2024届高三上学期10月月考数学(文)试题(已下线)第03讲 等比数列及其前n项和(练习)(已下线)考点5 等比数列的基本量及其性质 2024届高考数学考点总动员【练】四川省泸州市泸县第五中学2024届高三上学期期末数学(理)试题四川省泸州市泸县第五中学2024届高三上学期期末数学(文)试题(已下线)专题30 等比数列通项与前n项和宁夏吴忠市2024届高三下学期高考模拟联考(一)理科数学试题(已下线)6.3 等比数列及其前n项和课前·考点引领基础再现(已下线)5.2 等差数列和等比数列(高考真题素材之十年高考)(已下线)专题05 数列小题(7类题型,文科)专题18数列选择填空题(已下线)五年全国文科专题08数列选择填空题云南省昆明市第三中学2024届高三上学期数学第一次综合测试数学试卷山西省运城市景胜中学2020-2021学年高二上学期入学摸底数学试题江苏省扬州大学附属中学东部分校2020-2021学年高二上学期第一次模块学习效果调查数学试题江苏省宿迁市沭阳如东中学2020-2021学年高二上学期期中数学试题江苏省苏州市西安交大附中2020-2021学年高二上学期期中数学试题(已下线)4.3 等比数列(精讲)-2020-2021学年一隅三反系列之高二数学新教材选择性必修第二册(人教A版)江苏省盐城市东台中学2020-2021学年高二上学期期中数学试题(已下线)第04章 数列(A卷基础卷)-2020-2021学年高二数学选择性必修第二册同步单元AB卷(新教材人教A版)(已下线)第四章 数列(高考真题)-2020-2021学年高二数学单元复习(人教A版2019选择性必修第二册)宁夏吴忠市青铜峡市高级中学2020-2021学年高一下学期期末数学试题安徽省合肥市肥东县第二中学2020-2021学年高二下学期期末文科数学试题甘肃省金昌市永昌县第一高级中学2020-2021学年高一下学期期中数学试题江苏省泰州市泰兴市黄桥中学2020-2021学年高二上学期质量检测(一)数学试题新疆皮山县高级中学2020-2021学年高一下学期期中考试数学试题江西省南昌市豫章中学2021-2022学年高二入学调研(B)数学(文)试题苏教版(2019) 选修第一册 必杀技 第四章 素养检测人教A版(2019) 选修第二册 突围者 第四章 章末培优专练苏教版(2019) 选修第一册 突围者 第4章 章末培优专练第五章 数列(基础过关)-2020-2021学年高二数学单元测试定心卷(人教B版2019选择性必修第三册)江西省新余市第四中学2021-2022学年高二上学期第一次月考数学(文)试题北师大版(2019) 选修第二册 突围者 第一章 数列 章末培优专练西藏自治区拉萨市拉萨中学2021-2022学年高二上学期第二次月考数学试题西藏拉萨那曲高级中学2021-2022学年高二上学期期中考试数学试题(已下线)专题10 《数列》中的高考真题训练)-2021-2022学年高二数学同步培优训练系列(苏教版2019选择性必修第一册)山东省枣庄市2021-2022学年高二上学期期末数学试题人教B版(2019) 选修第三册 必杀技 第五章 5.3.1 等比数列(已下线)第04讲 复习课-数列-【寒假自学课】2022年高二数学寒假精品课(苏教版2019选择性必修第二册)(已下线)专题1.1 数列 章末检测1(易)-【满分计划】2021-2022学年高二数学阶段性复习测试卷(人教A版2019选择性必修第二册)江苏省南京市中华中学2021-2022学年高二上学期12月月考数学试题广东省佛山市狮山高级中学2021-2022学年高二下学期第一次教学质量检测数学试题黑龙江省鹤岗市第一中学2021-2022学年高二下学期第一次月考数学试题新疆乌鲁木齐市第八中学2021-2022学年高二下学期期中考试数学(文)试题陕西省西安市长安区第一中学2021-2022学年高一下学期第二次质量检测数学试题广东省佛山市南海区南海中学2021-2022学年高二下学期第二次大测数学试题湘教版(2019) 选修第一册 突围者 第1章 章末培优专练湘教版(2019) 选修第一册 突围者 第1章 章末培优专练2023版 苏教版(2019) 选修第一册 突围者 第4章 章末培优专练福建省莆田华侨中学2022-2023学年高二上学期期中考试数学试题甘肃省白银市第十中学2022-2023学年高二上学期期中考试数学试题甘肃省酒泉市玉门市玉门油田第一中学2022-2023学年高二上学期期中数学试题广东省广州市第九十七中学2022-2023学年高二上学期期末数学试题吉林省长春市第十七中学2022-2023学年高二上学期期末数学试题广东省人大附中深圳学校2022-2023学年高二上学期期末数学试题甘肃省张掖市2022-2023学年高二下学期第一次全市联考数学试题安徽省滁州市定远县育才学校2022-2023学年高二下学期第一次月考数学试题北京市八一学校2022-2023学年高二下学期3月月考数学试题湖南省长沙市芙蓉高级中学2022-2023学年高二上学期期中数学试题新疆兵团第三师图木舒克市鸿德实验学校2022-2023学年高二下学期第一次月考数学试题安徽省安庆市第九中学2022-2023学年高二下学期期中数学试卷新疆维吾尔自治区乌鲁木齐市第三十一中学2022-2023学年高二下学期期中数学试题新疆维吾尔自治区乌鲁木齐市第101中学2022-2023学年高二下学期期中数学试题甘肃省平凉市第二中学2022-2023学年高二下学期第二次月考数学试题云南省曲靖市师宗平高学校2023-2024学年高二上学期12月月考数学试题广东省广州市铁一中学、广州外国语学校、广大附中2023-2024学年高二上学期期末三校联考数学试题河北省石家庄市2023-2024学年高二上学期期末教学质量检测数学试题广东省揭阳市惠来县第一中学2023-2024学年高二下学期3月月考数学试题【课后练】 1.3.1 等比数列及其通项公式+1.3.2 等比数列与指数函数 课后作业-湘教版(2019)选择性必修第一册 第1章 数列福建省泉州市安溪一中、惠安一中、养正中学、泉州实验中学2023-2024学年高二下学期7月期末联考数学试题
8 . 数列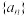 中,
中, ,对任意
,对任意  ,若
,若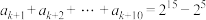 ,则
,则  ( )
( )
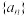 中,
中, ,对任意
,对任意  ,若
,若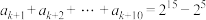 ,则
,则  ( )
( )| A.2 | B.3 | C.4 | D.5 |
您最近一年使用:0次
2020-07-08更新
|
39399次组卷
|
115卷引用:专题09 数列与数学归纳法-2021年浙江省高考数学命题规律大揭秘【学科网名师堂】
(已下线)专题09 数列与数学归纳法-2021年浙江省高考数学命题规律大揭秘【学科网名师堂】(已下线)考点21 等比数列及其前n项和-备战2022年高考数学一轮复习考点帮(浙江专用)2020年全国统一高考数学试卷(理科)(新课标Ⅱ)专题05+数列-2021高考数学(理)高频考点、热点题型归类强化(已下线)专题06 等比数列-2020年高考数学(理)母题题源解密(全国Ⅱ专版)(已下线)专题08 数列-五年(2016-2020)高考数学(理)真题分项(已下线)考点19 数列通项与求和与通项-2021年高考数学三年真题与两年模拟考点分类解读(新高考地区专用)(已下线)专题18 等差数列与等比数列-十年(2011-2020)高考真题数学分项(已下线)考点18 等差数列与等比数列的基本量-2021年高考数学三年真题与两年模拟考点分类解读(新高考地区专用)(已下线)考点20 等差数列与等比数列-2021年新高考数学一轮复习考点扫描(已下线)第13练 等比数列与求和-2021年高考数学一轮复习小题必刷(山东专用)(已下线)专题6.3 等比数列及其前n项和(精讲)-2021届高考数学(文)一轮复习讲练测(已下线)专题7.4 数列求和(练)-2021年新高考数学一轮复习讲练测(已下线)专题7.4 数列求和(精练)-2021年新高考数学一轮复习学与练(已下线)专题6.3 等比数列及其前n项和(精讲)-2021届高考数学(理)一轮复习讲练测(已下线)第23练 等比数列-2021年高考数学(理)一轮复习小题必刷河南省郑州市第一中学2020-2021学年高三上学期期中数学(文)试题湖南省邵阳市邵东市第一中学2020-2021学年高三上学期第五次月考数学试题(已下线)热点08 数列与不等式-2021年高考数学【热点·重点·难点】专练(新高考)(已下线)专题07 数列(讲)-2021年高考数学二轮复习讲练测(新高考版)(已下线)专题07 数列(讲)-2021年高考数学二轮复习讲练测(文理通用)(已下线)重组卷04-冲刺2021年高考数学(文)之精选真题+模拟重组卷(新课标卷)(已下线)专题07 数列的应用-备战2021年高考数学(理)经典小题考前必刷集合(已下线)专题06 数列-备战2021年高考数学(理)纠错笔记(已下线)专题13 数列-备战2021年新高考数学纠错笔记 (已下线)押第6题 数列-备战2021年高考数学(文)临考题号押题(全国卷2)(已下线)解密10 等差数列、等比数列(分层训练)-【高频考点解密】2021年高考数学(理)二轮复习讲义+分层训练(已下线)押第14题 数列小题-备战2021年高考数学(理)临考题号押题(全国卷2)(已下线)考点37 等比数列-备战2021年高考数学经典小题考前必刷(新高考地区专用)(已下线)专题29等比数列通项与前n项和-2022年(新高考)数学高频考点+重点题型(已下线)第28讲 等比数列及其前n项和(讲)- 2022年高考数学一轮复习讲练测(课标全国版)(已下线)考点02 等比数列-2022年高考数学(理)一轮复习小题多维练(全国通用)(已下线)考点16 等比数列及其前n项和-备战2022年高考数学(理)一轮复习考点微专题(已下线)考点23 等比数列及其前n项和-备战2022年高考数学(理)一轮复习考点帮(已下线)“8+4+4”小题强化训练(30)等比数列及其前n项和-2022届高考数学一轮复习(江苏等新高考地区专用)(已下线)专题07 数列及其应用-十年(2012-2021)高考数学真题分项汇编(全国通用)(已下线)考点42 数列的递推关系与通项公式-备战2022年高考数学一轮复习考点帮(新高考地区专用)【学科网名师堂】(已下线)6.2 等比数列(精讲)-【一隅三反】2022年高考数学一轮复习(新高考地区专用)(已下线)专题7.4 数列求和(练)- 2022年高考数学一轮复习讲练测(新教材新高考)(已下线)专题18等比数列-2022年高三毕业班数学常考点归纳与变式演练(文理通用)山西省运城市2022届高三上学期期中数学(文)试题(已下线)2020年高考全国2数学理高考真题变式题6-10题(已下线)专题11 有关等差(比)数列的基本运算——备战2022年高考数学二轮复习常考点专题突破(已下线)专题22 等差等比数列性质的巧用-学会解题之高三数学万能解题模板【2022版】河南省新乡市原阳县第一高级中学2021-2022学年高三上学期12月月考数学(理)试题河南省新乡市原阳县第一高级中学2021-2022学年高三上学期12月月考数学(文)试题(已下线)专题08 数列小题大做-备战2022年高考数学冲刺横向强化精练精讲(新高考专用)(已下线)类型二 等比数列-【题型突破】备战2022年高考数学二轮基础题型+重难题型突破(新高考专用)(已下线)专题24 真题优选重组第一卷-备战2022年高考数学冲刺横向强化精练精讲(新高考专用)(已下线)查补易混易错点10 数列-【查漏补缺】2022年高考数学(理)三轮冲刺过关(已下线)2022年高考考前20天终极冲刺攻略(三)【数学】(新高考地区专用)(5月31日)(已下线)押全国卷(理科)第5,9题 数列-备战2022年高考数学(理)临考题号押题(全国卷)(已下线)专题21 等比数列-2023届高考数学一轮复习精讲精练(新高考专用)(已下线)专题05 数列选填题(已下线)8.2 等比数列(已下线)考向20等比数列及其前n项和(重点) - 3(已下线)第03讲 等比数列及其前n项和 (高频考点—精讲)-2四川省成都市成都市石室中学2022-2023学年高三上学期期中数学理科试题河南省郑州市京师杜甫高级中学2022-2023高三上学期第四次考试数学试题吉林省白山市抚松县第一中学2022-2023学年高三上学期第三次校内模拟数学试题(已下线)模块三 专题5 数列(已下线)专题16 等比数列-3(已下线)重组卷02(理科)(已下线)专题11 押全国卷(理科)第4、8题 数列(已下线)专题14 数列的通项公式(已知递推式)-3上海市曹杨第二中学2023届高三5月模拟2数学试题(已下线)拓展五:近五年数列高考真题分类汇编(2)全国甲乙卷5年真题分类汇编《数列》选填题河南省信阳高级中学2023届高三下学期高考考前测试文科数学试题(已下线)第三节 等比数列 核心考点集训安徽省安庆市第二中学东区2021-2022学年高三上学期12月月考理科数学试题内蒙古呼伦贝尔市满洲里远方中学2023-2024学年高三上学期第一次模拟考试理科数学试题四川省绵阳市三台中学2024届高三一模数学(理)试题(一)甘肃省庆阳市宁县第二中学2024届高三第三次月考数学试题(已下线)考点4 等比数列的定义与判断 2024届高考数学考点总动员【练】(已下线)专题05 数列 第二讲 数列的求和(分层练)(已下线)专题30 等比数列通项与前n项和(已下线)第六章 数列6.3 等比数列及其前n项和(已下线)专题06 数列小题(理科)-2专题17数列选择填空题(第二部分)(已下线)五年全国理科专题08数列选择填空题(已下线)5.2 等比数列(讲义)(已下线)第02章等比数列(B卷提升卷)-2020-2021学年高二数学必修五同步单元AB卷(苏教版,新课改地区专用)河北省石家庄市第二中学2020-2021学年高二上学期8月线上考试(二)数学试题(已下线)第四章 数列测试 A基础练广西平果第三高级中学2020-2021学年高一下学期第一次月考数学试题苏教版(2019) 选修第一册 必杀技 第四章 素养检测人教A版(2019) 选修第二册 突围者 第四章 章末培优专练(已下线)4.3.2 等比数列前n项和2课时陕西省西安市长安区第一中学2021-2022学年高二上学期9月第一次质量检测理科数学试题北师大版(2019) 选修第二册 突围者 第一章 数列 章末培优专练(已下线)第4章 数列(培优卷)-2021-2022学年高二数学新教材单元双测卷(苏教版2019选择性必修第一册)(已下线)4.3.3 等比数列的前n项和(课堂培优)-2021-2022学年高二数学课后培优练(苏教版2019选择性必修第一册)江苏省苏州市高新区第一中学2021-2022学年高二上学期期中模拟数学试题河北省唐山市第一中学2021-2022学年高二上学期12月月考数学试题江苏省南京市金陵中学2021-2022学年高二上学期12月月考数学试题(已下线)专题10 《数列》中的高考真题训练)-2021-2022学年高二数学同步培优训练系列(苏教版2019选择性必修第一册)广东省茂名市电白区2021-2022学年高二上学期期末数学试题(已下线)4.3等比数列A卷安徽省亳州市第一中学2021-2022学年高二下学期3月月考数学试题(已下线)第04讲 复习课-数列-【寒假自学课】2022年高二数学寒假精品课(苏教版2019选择性必修第二册)湘教版(2019) 选修第一册 突围者 第1章 章末培优专练湘教版(2019) 选修第一册 突围者 第1章 章末培优专练2023版 苏教版(2019) 选修第一册 突围者 第4章 章末培优专练2023版 湘教版(2019) 选修第一册 过关斩将 第1章 综合拔高练2023版 苏教版(2019) 选修第一册 名师精选卷 第十一单元 等比数列 A卷福建省华安县第一中学2022-2023学年高二上学期第一次月考数学试题陕西省榆林市神木中学2021-2022学年高二上学期第一次检测考试数学试题安徽省滁州市定远县育才学校2021-2022学年高二下学期第二次月考数学试题(已下线)第5讲 等比数列的前 项和及性质6大题型总结 (1)河南省南阳市第二中学校2022-2023学年高二下学期3月月考数学试题河南省三门峡市2022-2023学年高二上学期期末数学试题天津市咸水沽第一中学2023-2024学年高二上学期第二次月考(12月)数学试卷湖南省株洲市炎陵县2023-2024学年高二下学期入学素质考试数学试题四川省绵阳中学2023-2024学年高二下学期4月月考数学试题
名校
9 . 已知各项均为正数的等比数列{an}的前n项和为Sn,且满足a6,3a4,-a5成等差数列,则 =( )
=( )
 =( )
=( )| A.3 | B.9 |
| C.10 | D.13 |
您最近一年使用:0次
2020-08-22更新
|
1309次组卷
|
15卷引用:2024届浙江省丽水、湖州、衢州三地市二模数学试卷
2024届浙江省丽水、湖州、衢州三地市二模数学试卷【全国校级联考】广东省汕头市潮南区2018届高考(5月)冲刺数学(理)试题【全国百强校】河北省武邑中学2019届高三12月月考数学(文)试题2020届广东省梅州市五华县高三上学期期末数学(理)试题2019届湖北省黄冈中学高三适应性考试数学(文)试题山西省实验中学2019-2020学年高三下学期3月开学摸底数学(文)试题安徽省淮北市第一中学2019-2020学年高三下学期第五次考试数学(理)试题(已下线)专题6.3 等比数列及其前n项和-2021年高考数学(理)一轮复习-题型全归纳与高效训练突破(已下线)专题6.3 等比数列及其前n项和-2021年高考数学(文)一轮复习-题型全归纳与高效训练突破山东省菏泽第一中学人民路校区2024届高三下学期3月月考数学试题广东省茂名市高2024届高三下学期高考模拟数学试题福建省漳州市第三中学2024届高三下学期高考全真模拟考试数学试题湖北省武汉市黄陂区第七高级中学2024届高三模拟考试(二)数学试题湖南省长沙市长郡中学2019-2020学年高一下学期“停课不停学”线上教学效果检测考试数学试题江西省萍乡市芦溪中学2021-2022学年高二上学期第二次段考数学(理)试题
名校
解题方法
10 . 已知正项等比数列{an}的前n项和为Sn,且S8-2S4=5,则a9+a10+a11+a12的最小值为( )
| A.10 | B.15 | C.20 | D.25 |
您最近一年使用:0次
2020-11-16更新
|
2277次组卷
|
14卷引用:浙江省杭州地区四校2018-2019学年高三上学期联考数学试题
浙江省杭州地区四校2018-2019学年高三上学期联考数学试题河南省郑州市第一中学2017-2018上期高三理科数学一轮复习周末测试卷试题河南省林州市第一中学2018届高三8月调研考试理科数学试题河北省石家庄市第二中学2018届高三12月月考数学(理)试题皖江名校2018届高三12月份大联考数学(理)试题广东省广州市广大附属实验学校2018届高三8月份调研数学试题(已下线)专题6.3 等比数列及其前n项和(精练)-2021届高考数学(理)一轮复习讲练测(已下线)考点22 不等式、一元二次不等式与基本不等式-2021年新高考数学一轮复习考点扫描(已下线)解密03 等差数列与等比数列(讲义)-【高频考点解密】2021年新高考数学二轮复习讲义+分层训练(已下线)第03讲 等比数列及前n项和(讲)(已下线)8.2 等比数列(已下线)专题6-1 等差数列,等比数列中性质应用(选填)-2(已下线)2023年新课标全国Ⅱ卷数学真题变式题6-10云南省开远市第一中学校2023届高三下学期6月月考数学试题



