1 . 已知正方体 的棱长为1,从正方体的8个顶点中选出4个点构成一个体积大于
的棱长为1,从正方体的8个顶点中选出4个点构成一个体积大于 的三棱锥,则这4个点可以是
的三棱锥,则这4个点可以是________ .(写出一组即可)
 的棱长为1,从正方体的8个顶点中选出4个点构成一个体积大于
的棱长为1,从正方体的8个顶点中选出4个点构成一个体积大于 的三棱锥,则这4个点可以是
的三棱锥,则这4个点可以是
您最近一年使用:0次
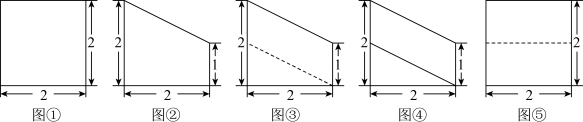
2 . 若某几何体为一个棱长为2的正方体被过顶点P的平面截去一部分后所剩余的部分,且该几何体以图①为俯视图,其正视图和侧视图为图②③④⑤中的两个,则正视图和侧视图的编号依次为______ (写出符合要求的一组答案即可).



您最近一年使用:0次
名校
解题方法
3 . 正多面体又称柏拉图多面体,被喻为最有规律的立体结构,其所有面都只由一种正多边形构成,正多面体共有五种,它们分别是正四面体、正六面体、正八面体、正十二面体和正二十面体,连接棱长为2的正方体的六个面的中心,即可得到一个正八面体,则该正八面体的内切球的表面积为______ .
您最近一年使用:0次
2023-08-24更新
|
610次组卷
|
5卷引用:贵州省天柱民族中学2024届高三上学期第一次月考数学试题
贵州省天柱民族中学2024届高三上学期第一次月考数学试题云南师范大学附属中学2024届高三高考适应性月考卷(二)数学试题(已下线)专题突破卷18 外接球和内切球(已下线)考点7 组合体的内切 2024届高考数学考点总动员【练】云南省昆明市云南师范大学附属中学2024届高三上学期适应性月考(二)数学试题
解题方法
4 . 已知三棱锥 的外接球半径为
的外接球半径为 ,且
,且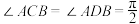 ,
, .在下列条件中,能使三棱锥
.在下列条件中,能使三棱锥 的体积为定值的有
的体积为定值的有______ ;其体积可能为______ .(写出一个可能的值即可)
①直线 与平面
与平面 所成角为
所成角为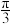 ;②
;② ;
;
③二面角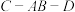 的大小为
的大小为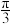 ;④
;④ .
.
 的外接球半径为
的外接球半径为 ,且
,且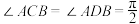 ,
, .在下列条件中,能使三棱锥
.在下列条件中,能使三棱锥 的体积为定值的有
的体积为定值的有①直线
 与平面
与平面 所成角为
所成角为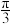 ;②
;② ;
;③二面角
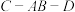 的大小为
的大小为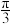 ;④
;④ .
.
您最近一年使用:0次
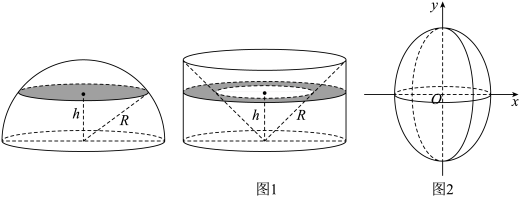
5 . 现介绍祖暅原理求球体体积公式的做法:可构造一个底面半径和高都与球半径相等的圆柱,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,用这样一个几何体与半球对应,应用祖暅原理(图1),即可求得球的体积公式.已知椭圆的标准方程为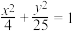 ,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于( )
,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于( )
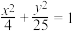 ,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于( )
,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于( )
A.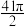 | B.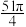 | C.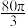 | D.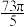 |
您最近一年使用:0次
真题
名校
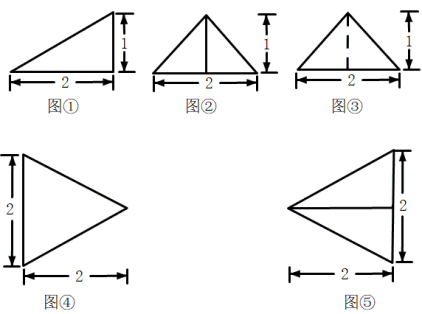
6 . 以图①为正视图,在图②③④⑤中选两个分别作为侧视图和俯视图,组成某个三棱锥的三视图,则所选侧视图和俯视图的编号依次为_________ (写出符合要求的一组答案即可).

您最近一年使用:0次
2021-06-07更新
|
35860次组卷
|
39卷引用:2021年全国高考乙卷数学(文)试题
2021年全国高考乙卷数学(文)试题2021年全国高考乙卷数学(理)试题(已下线)考点29 空间几何体的表面积与体积-备战2022年高考数学一轮复习考点帮(浙江专用)(已下线)考点01三视图-2022年高考数学(理)一轮复习小题多维练(全国通用)(已下线)考点30 空间几何体的结构及其三视图与直观图-备战2022年高考数学(理)一轮复习考点帮(已下线)专题10 三视图-十年(2012-2021)高考数学真题分项汇编(全国通用)(已下线)专题04 立体几何-2021年高考真题和模拟题数学(文)分项汇编(全国通用)(已下线)专题8.1 空间几何体及其三视图和直观图(练)- 2022年高考数学一轮复习讲练测(新教材新高考)(已下线)专题04 立体几何-五年(2017-2021)高考数学真题分项汇编(文科+理科)(已下线)专题04 立体几何-2021年高考真题和模拟题数学(理)专项汇编(全国通用)(已下线)专题22空间几何体的三视图、表面积和体积-2022年高三毕业班数学常考点归纳与变式演练(文理通用)(已下线)考向22 空间几何体-备战2022年高考数学一轮复习考点微专题(上海专用)(已下线)2021年高考全国乙卷数学(理)高考真题变式题11-15题(已下线)2021年全国高考乙卷数学(文)试题变式题16-19题(已下线)专题06几何体表面积体积与球切、接的问题(练)(理科)第一篇 热点、难点突破篇-《2022年高考理科数学二轮复习讲练测》(全国课标版)(已下线)专题09 几何体的面积与体积问题(讲)--第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测(浙江专用)》(已下线)专题15立体几何(文科)小题大做-备战2022年高考数学冲刺横向强化精练精讲(已下线)查补易混易错点06 立体几何-【查漏补缺】2022年高考数学(理)三轮冲刺过关(已下线)押全国卷(文科)第8,16题 立体几何小题-备战2022年高考数学(文)临考题号押题(全国卷)(已下线)押全国卷(理科)第8,16题 立体几何小题-备战2022年高考数学(理)临考题号押题(全国卷)(已下线)专题19 立体几何多选、填空题(已下线)专题16 立体几何选填题-2(已下线)考点7-2 三视图、截面与外接球 (文理)(已下线)2021年高考全国乙卷数学(理)高考真题变式题16-20题2023届甘肃省高考数学模拟试卷(一)(已下线)专题4 劣构题题型(已下线)专题04 押全国卷(文科)9,12小题 立体几何(已下线)专题05 押全国卷(理科)7,9小题 立体几何全国甲乙卷3年真题分类汇编《立体几何》选填题全国甲乙卷真题5年分类汇编《立体几何》选填全国甲乙卷5年真题分类汇编《立体几何》选填题(已下线)专题10 空间向量与立体几何-1(已下线)专题14 立体几何填空题(文科)(已下线)专题15 立体几何多选、填空题(理科)专题18立体几何与空间向量选择填空题(第一部分)专题19立体几何与空间向量选择填空题(第一部分)(已下线)五年全国文科专题09立体几何与空间向量选择填空题(已下线)五年全国理科专题09立体几何与空间向量选择填空题陕西省西安中学2021-2022学年高一上学期12月第二次月考数学试题
7 . 现介绍祖暅原理求球体体积公式的做法:可构造一个底面半径和高都与球半径相等的圆柱,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,用这样一个几何体与半球应用祖暅原理(图 ),即可求得球的体积公式.请研究和理解球的体积公式求法的基础上,解答以下问题:已知椭圆的标准方程为
),即可求得球的体积公式.请研究和理解球的体积公式求法的基础上,解答以下问题:已知椭圆的标准方程为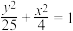 ,将此椭圆绕
,将此椭圆绕 轴旋转一周后,得一橄榄状的几何体(图
轴旋转一周后,得一橄榄状的几何体(图 ),其体积等于
),其体积等于______ .
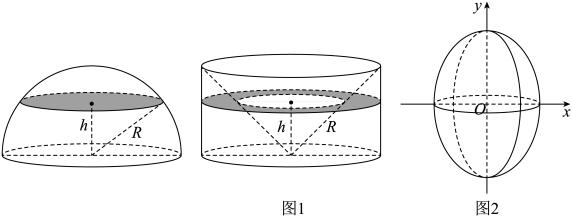
 ),即可求得球的体积公式.请研究和理解球的体积公式求法的基础上,解答以下问题:已知椭圆的标准方程为
),即可求得球的体积公式.请研究和理解球的体积公式求法的基础上,解答以下问题:已知椭圆的标准方程为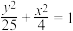 ,将此椭圆绕
,将此椭圆绕 轴旋转一周后,得一橄榄状的几何体(图
轴旋转一周后,得一橄榄状的几何体(图 ),其体积等于
),其体积等于
您最近一年使用:0次
2017-03-21更新
|
3251次组卷
|
7卷引用:2017届全国各地高三最新模拟文化试题集数学试卷
8 . 如图,已知多面体 的底面
的底面 是边长为2的菱形,
是边长为2的菱形, ,
,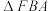 是等边三角形,且平面
是等边三角形,且平面 底面
底面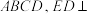 底面
底面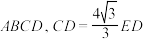 .
.
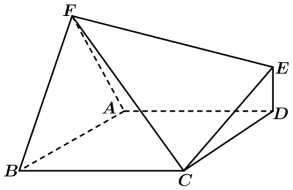
(1)在平面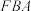 内找到一个点G,使得
内找到一个点G,使得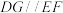 ,只需说明作法即可,不必说明理由;
,只需说明作法即可,不必说明理由;
(2)求(1)中确定点G到平面 的距离.
的距离.
 的底面
的底面 是边长为2的菱形,
是边长为2的菱形, ,
,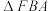 是等边三角形,且平面
是等边三角形,且平面 底面
底面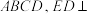 底面
底面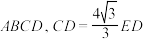 .
.
(1)在平面
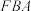 内找到一个点G,使得
内找到一个点G,使得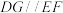 ,只需说明作法即可,不必说明理由;
,只需说明作法即可,不必说明理由;(2)求(1)中确定点G到平面
 的距离.
的距离.
您最近一年使用:0次
9 . 若某几何体为一个棱长为 的正方体被过顶点
的正方体被过顶点 的平面截去一部分后所剩余的部分,且该几何体以图①为俯视图,其正视图和侧视图为图②③④⑤⑥中的两个,则正视图和侧视图的编号依次为
的平面截去一部分后所剩余的部分,且该几何体以图①为俯视图,其正视图和侧视图为图②③④⑤⑥中的两个,则正视图和侧视图的编号依次为______ (填第一组),______ (填第二组).(写出符合要求的两组编号即可)



 的正方体被过顶点
的正方体被过顶点 的平面截去一部分后所剩余的部分,且该几何体以图①为俯视图,其正视图和侧视图为图②③④⑤⑥中的两个,则正视图和侧视图的编号依次为
的平面截去一部分后所剩余的部分,且该几何体以图①为俯视图,其正视图和侧视图为图②③④⑤⑥中的两个,则正视图和侧视图的编号依次为


您最近一年使用:0次
2021-09-08更新
|
149次组卷
|
4卷引用:甘肃省白银市靖远县2021-2022学年高三上学期开学考试数学(文科)试题
甘肃省白银市靖远县2021-2022学年高三上学期开学考试数学(文科)试题甘肃省白银市靖远县2021-2022学年高三上学期开学考试数学(理科)试题(已下线)考点27 三视图与直观图-备战2022年高考数学典型试题解读与变式(已下线)专题04 分类讨论型【练】【北京版】
名校
解题方法
10 . (1)一个正方体纸盒展开后如图所示,在原正方体纸盒中有如下结论: ;②
;② ;③
;③ 与
与 是异面直线;④
是异面直线;④ ;
;
以上四个结论中,正确结论的序号是哪些?(无需说明理由,只要写出正确结论的序号即可)
(2)如图,四面体 中,
中, ,且直线
,且直线 与
与 成60°角,点M、N分别是
成60°角,点M、N分别是 、
、 的中点,求异面直线
的中点,求异面直线 和
和 所成角的大小.
所成角的大小.
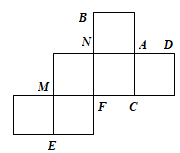
 ;②
;② ;③
;③ 与
与 是异面直线;④
是异面直线;④ ;
;以上四个结论中,正确结论的序号是哪些?(无需说明理由,只要写出正确结论的序号即可)
(2)如图,四面体
 中,
中, ,且直线
,且直线 与
与 成60°角,点M、N分别是
成60°角,点M、N分别是 、
、 的中点,求异面直线
的中点,求异面直线 和
和 所成角的大小.
所成角的大小.
您最近一年使用:0次
2020-10-11更新
|
596次组卷
|
5卷引用:上海市行知中学2021届高三上学期开学考试数学试题
上海市行知中学2021届高三上学期开学考试数学试题(已下线)课时40 空间直线与直线的位置关系-2022年高考数学一轮复习小题多维练(上海专用)(已下线)8.3 空间点、直线、平面之间的位置关系-2020-2021高中数学新教材配套提升训练(人教A版必修第二册)沪教版(2020) 必修第三册 新课改一课一练 阶段检测2【课堂练】 阶段复习2 随堂练习-沪教版(2020)必修第三册 第12章 概率初步



