名校
解题方法
1 . 如图,在空间几何体 中,平面
中,平面
 平面
平面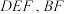

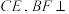 平面
平面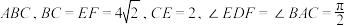 ,则几何体
,则几何体 的外接球的体积为
的外接球的体积为__________ .
 中,平面
中,平面
 平面
平面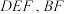

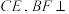 平面
平面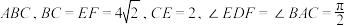 ,则几何体
,则几何体 的外接球的体积为
的外接球的体积为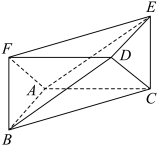
您最近一年使用:0次
名校
解题方法
2 . 已知圆台的上底面半径为1,下底面半径为5,侧面积为 ,则圆台的体积为
,则圆台的体积为______ ,若该圆台的上、下底面圆周均在球 的球面上,则球
的球面上,则球 的表面积为
的表面积为______ .
 ,则圆台的体积为
,则圆台的体积为 的球面上,则球
的球面上,则球 的表面积为
的表面积为
您最近一年使用:0次
名校
3 . 如图所示,四面体 的各棱长均为
的各棱长均为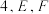 分别为棱
分别为棱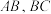 的中点,
的中点, 为棱
为棱 上异于顶点的点,则以下结论正确的为( )
上异于顶点的点,则以下结论正确的为( )
 的各棱长均为
的各棱长均为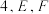 分别为棱
分别为棱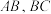 的中点,
的中点, 为棱
为棱 上异于顶点的点,则以下结论正确的为( )
上异于顶点的点,则以下结论正确的为( )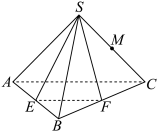
A. |
B.直线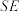 与 与 所成角的余弦值为 所成角的余弦值为 |
C.四面体 的外接球体积为 的外接球体积为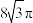 |
D.平面 截四面体所得的截面图形的周长最小值为8 截四面体所得的截面图形的周长最小值为8 |
您最近一年使用:0次
2024-06-14更新
|
547次组卷
|
3卷引用:2025届甘肃省张掖市某校高三下学期6月模拟考试数学试题
名校
解题方法
4 . 已知正四棱柱 中,
中,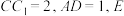 为
为 的中点,则平面
的中点,则平面 截此四棱柱的外接球所得的截面面积为
截此四棱柱的外接球所得的截面面积为__________ .
 中,
中,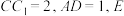 为
为 的中点,则平面
的中点,则平面 截此四棱柱的外接球所得的截面面积为
截此四棱柱的外接球所得的截面面积为
您最近一年使用:0次
名校
5 . 如图,为球形物品设计制作正四面体、正六面体、正八面体形状的包装盒,最少用料分别记为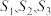 ,则它们的大小关系为( )
,则它们的大小关系为( )
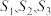 ,则它们的大小关系为( )
,则它们的大小关系为( )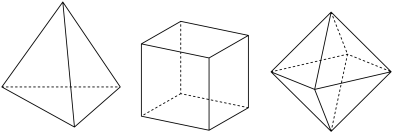
A. | B.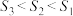 |
C.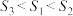 | D.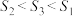 |
您最近一年使用:0次
2024-05-27更新
|
893次组卷
|
2卷引用:甘肃省兰州市西北师大附中2024届高三第五次诊断考试(三模)数学试题
6 . 已知圆锥PO的顶点为P,其三条母线PA,PB,PC两两垂直,且母线长为6,则圆锥PO的内切球表面职与圆锥侧面积之和为( )
A.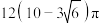 | B.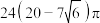 | C.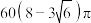 | D.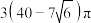 |
您最近一年使用:0次
2024-05-27更新
|
736次组卷
|
8卷引用:甘肃省兰州市第五十八中学2024届高三第二次高考仿真考试数学试题
甘肃省兰州市第五十八中学2024届高三第二次高考仿真考试数学试题湖北省部分学校2024届高三下学期新高考信息考试数学试题二(已下线)专题7 立体几何综合问题【练】(已下线)专题3 学科素养与综合问题(单选题8)(已下线)基本立体图形、简单几何体的表面积与体积01-一轮复习考点专练(已下线)模型6 外接球与内切球问题模型(第7章 立体几何与空间向量)(已下线)专题3.9 立体中的外接球和内切球-重难点突破及混淆易错规避(人教A版2019必修第二册)(已下线)6.6.3 球的表面积和体积-同步精品课堂(北师大版2019必修第二册)
名校
7 . 梯形 中,
中,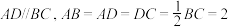 ,
,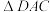 沿着
沿着 翻折,使点
翻折,使点 到点
到点 处,得到三棱锥
处,得到三棱锥 ,则下列说法正确的是( )
,则下列说法正确的是( )
 中,
中,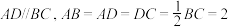 ,
,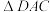 沿着
沿着 翻折,使点
翻折,使点 到点
到点 处,得到三棱锥
处,得到三棱锥 ,则下列说法正确的是( )
,则下列说法正确的是( )A.存在某个位置的点 ,使 ,使 平面 平面 |
B.若 的中点为 的中点为 ,则异面直线 ,则异面直线 与 与 所成角的大小和平面 所成角的大小和平面 与平面 与平面 所成角的大小相等 所成角的大小相等 |
C.若平面 平面 平面 ,则三棱锥 ,则三棱锥 外接球的表面积是 外接球的表面积是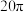 |
D.若 的中点为 的中点为 ,则必存在某个位置的点 ,则必存在某个位置的点 ,使 ,使 |
您最近一年使用:0次
2024-03-14更新
|
426次组卷
|
2卷引用:甘肃省2024届高三下学期3月月考(一模)数学试题
名校
解题方法
8 . 已知圆锥的高为 ,其顶点和底面圆周都在直径为
,其顶点和底面圆周都在直径为 的球面上,则圆锥的体积为
的球面上,则圆锥的体积为______ .
 ,其顶点和底面圆周都在直径为
,其顶点和底面圆周都在直径为 的球面上,则圆锥的体积为
的球面上,则圆锥的体积为
您最近一年使用:0次
2024-03-03更新
|
567次组卷
|
3卷引用:甘肃省兰州市第五十九中学2025届高三上学期建档模拟考试数学试卷
甘肃省兰州市第五十九中学2025届高三上学期建档模拟考试数学试卷山西省运城市盐湖区2024届高三下学期一模考试数学试题(已下线)重难点6-3 立体几何外接球与内切球问题(12题型+满分技巧+限时检测)
解题方法
9 . 在几何学中,截角立方体是一种十四面体,由八个正三角形与六个正八边形组成,共有 个面,
个面, 个顶点以及
个顶点以及 条边,是一种阿基米德立体,属于半正多面体.下图是一个所有棱长均为
条边,是一种阿基米德立体,属于半正多面体.下图是一个所有棱长均为 的截角立方体,则该截角立方体的外接球的表面积为
的截角立方体,则该截角立方体的外接球的表面积为_____ .
 个面,
个面, 个顶点以及
个顶点以及 条边,是一种阿基米德立体,属于半正多面体.下图是一个所有棱长均为
条边,是一种阿基米德立体,属于半正多面体.下图是一个所有棱长均为 的截角立方体,则该截角立方体的外接球的表面积为
的截角立方体,则该截角立方体的外接球的表面积为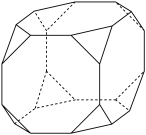
您最近一年使用:0次
2024-02-27更新
|
313次组卷
|
5卷引用:甘肃省张掖市2023-2024学年高三下学期第三次诊断考试数学试卷
甘肃省张掖市2023-2024学年高三下学期第三次诊断考试数学试卷1号卷·2022年高考最新原创信息试卷(六)文数1号卷·2022年高考最新原创信息试卷(六)理数(已下线)第六章 突破立体几何创新问题 专题二 交汇世界文化 微点2 与世界文化遗产有关的的立体几何问题综合训练【基础版】广东省汕尾市部分学校2023-2024学年高一下学期5月月考数学试卷
23-24高三上·江西·阶段练习
名校
解题方法
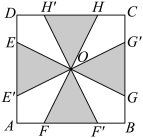
10 . 如图,在边长为 的正方形
的正方形 中剪掉四个阴影部分的等腰三角形,其中
中剪掉四个阴影部分的等腰三角形,其中 为正方形对角线的交点,
为正方形对角线的交点, ,将其余部分折叠围成一个封闭的正四棱锥,若该正四棱锥的内切球半径为
,将其余部分折叠围成一个封闭的正四棱锥,若该正四棱锥的内切球半径为 ,则该正四棱锥的表面积可能为( )
,则该正四棱锥的表面积可能为( )
 的正方形
的正方形 中剪掉四个阴影部分的等腰三角形,其中
中剪掉四个阴影部分的等腰三角形,其中 为正方形对角线的交点,
为正方形对角线的交点, ,将其余部分折叠围成一个封闭的正四棱锥,若该正四棱锥的内切球半径为
,将其余部分折叠围成一个封闭的正四棱锥,若该正四棱锥的内切球半径为 ,则该正四棱锥的表面积可能为( )
,则该正四棱锥的表面积可能为( )
A. | B.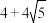 | C. | D. |
您最近一年使用:0次
2023-12-22更新
|
399次组卷
|
5卷引用:甘肃省武威市2024届高三上学期阶段调考数学试题
甘肃省武威市2024届高三上学期阶段调考数学试题(已下线)江西省“三新”协同教研共同体2024届高三上学期12月联考数学试题江西省部分学校2024届高三上学期12月联考数学试题(已下线)第04讲 8.3.1 棱柱、棱锥、棱台的表面积和体积-【帮课堂】(人教A版2019必修第二册)(已下线)第17讲 第八章 立体几何初步 章末重点题型大总结-【帮课堂】(人教A版2019必修第二册)



