1 . 如图①,在等腰梯形 中,
中, ,
,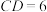 ,
,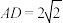 ,
, ,
, 分别是线段
分别是线段 的两个三等分点,若把等腰梯形沿虚线
的两个三等分点,若把等腰梯形沿虚线 ,
, 折起,使得点
折起,使得点 和点
和点 重合,记为点
重合,记为点 ,如图②.
,如图②.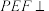 平面
平面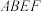 ;
;
(2)求平面 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
 中,
中, ,
,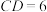 ,
,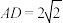 ,
, ,
, 分别是线段
分别是线段 的两个三等分点,若把等腰梯形沿虚线
的两个三等分点,若把等腰梯形沿虚线 ,
, 折起,使得点
折起,使得点 和点
和点 重合,记为点
重合,记为点 ,如图②.
,如图②.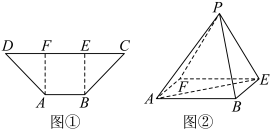
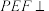 平面
平面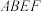 ;
;(2)求平面
 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
您最近一年使用:0次
2024-07-18更新
|
199次组卷
|
12卷引用:陕西省汉中市龙岗学校2019-2020学年高二上学期期末考试数学(理)试题
陕西省汉中市龙岗学校2019-2020学年高二上学期期末考试数学(理)试题山西省长治市太行中学2018-2019学年高二下学期期末数学(理)试题吉林省长春市汽车经济技术开发区第三中学2023-2024学年高二下学期7月期末考试数学试题【市级联考】湖南省株洲市2019届高三教学质量统一检测(一)理科数学试题湖北省十堰市2019届高三模拟试题理科数学学科安徽省滁州市2019-2020学年高二上学期第二次月考数学试题(已下线)专题02 从空间到平面,助力破解立体几何问题 (第四篇)-2020高考数学压轴题命题区间探究与突破江苏省宿迁市泗洪县洪翔中学2019-2020学年高一下学期第一次月考数学试题山西省山西大学附中2018-2019学年高三下学期3月模块诊断数学(理)试题(已下线)第37讲 立体几何中的向量方法 (练) — 2022年高考数学一轮复习讲练测(课标全国版)(已下线)2021年新高考浙江数学高考真题变式题17-22题(已下线)压轴题06 空间向量与立体几何4大类型专练-【常考压轴题】(人教B版2019选择性必修第一册)
名校
2 . 在三棱锥 中,
中, 是边长为4的正三角形,平面
是边长为4的正三角形,平面 平面
平面 ,
, ,
, 分别为
分别为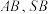 的中点.
的中点.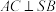 ;
;
(2)求二面角 的正弦值的大小.
的正弦值的大小.
 中,
中, 是边长为4的正三角形,平面
是边长为4的正三角形,平面 平面
平面 ,
, ,
, 分别为
分别为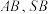 的中点.
的中点.
 ;
;(2)求二面角
 的正弦值的大小.
的正弦值的大小.
您最近一年使用:0次
2024-01-07更新
|
1989次组卷
|
16卷引用:吉林省辽源市田家炳高中友好学校2024届高三上学期第七十六届期末联考数学试题
吉林省辽源市田家炳高中友好学校2024届高三上学期第七十六届期末联考数学试题江苏省扬州市邗江中学2019-2020学年高二(新疆班)下学期期中数学试题四川省成都市2023-2024学年高二上学期期末练习数学试题(3)河南省郑州市第十八中学2023-2024学年高二上学期期末模拟数学试题(三)陕西省西安市陕西师范大学附属中学渭北中学2023届高三三模理科数学试题黑龙江省哈尔滨市兆麟中学2023-2024学年高二上学期第一次月考数学试题江苏省南京市六校联合体2023-2024学年高三上学期10月联合调研数学试题浙江省杭州市富阳区实验中学2023-2024学年高二上学期9月摸底考试数学试题上海市市西中学2024届高三上学期期中数学试题福建泉州城东中学、南安华侨中学、石狮八中、福建泉州外国语学校四校2023-2024学年高二上学期期中考试数学试卷广东省广州市广东实验中学2024届高三上学期大湾区数学冲刺卷(三)湖南省长沙市雅礼中学2024届高三月考试卷数学(六)广东番禺中学2023-2024学年高三第六次段考数学试题广东省广州市番禺中学2024届高三第六次段考数学试题(已下线)作业06 暑期培优必刷压轴题-【暑假分层作业】(苏教版2019选择性必修第二册)广东省湛江市岭南师范学院附属中学2023-2024学年高二下学期第二次段数学试题
名校
3 . 如图,在正方体 中,点P在线段
中,点P在线段 上运动,则下列结论正确的是( )
上运动,则下列结论正确的是( )
 中,点P在线段
中,点P在线段 上运动,则下列结论正确的是( )
上运动,则下列结论正确的是( )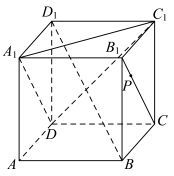
A.直线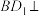 平面 平面 |
B.三棱锥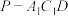 的体积为定值 的体积为定值 |
C.异面直线 与 与 所成角的取值范围是 所成角的取值范围是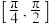 |
D.直线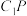 与平面 与平面 所成角的正弦值的最大值为 所成角的正弦值的最大值为 |
您最近一年使用:0次
2023-05-16更新
|
6737次组卷
|
82卷引用:山东省烟台市2019-2020学年高三上学期期末考试数学试题
山东省烟台市2019-2020学年高三上学期期末考试数学试题吉林省长春吉大附中实验学校2021-2022学年高二上学期期末数学试题(已下线)必刷卷10-2020年高考数学必刷试卷(新高考)【学科网名师堂】-《2020年新高考政策解读与配套资源》(已下线)专题09 立体几何初步-备战2020年新高考数学新题型之【多选题】-《2020年新高考政策解读与配套资源》(已下线)卷03-备战2020年新高考数学自学检测黄金10卷-《2020年新高考政策解读与配套资源》(已下线)备战2020年高考数学之考场再现(山东专版)09山东师范大学附属中学2020-2021学年高二10月月考数学试题山东省日照第一中学2020-2021学年高三第二次联合考试数学试题(已下线)高二上学期期末综合测试二+(B卷提升卷)-2020-2021学年高二数学上学期同步单元AB卷(苏教版,新课改地区专用)广东省汕头市金山中学2020-2021学年高二上学期期末数学试题江苏省盐城市滨海中学2020-2021学年高三上学期第三次阶段学情检测数学试题辽宁省沈阳市重点高中协作体2021-2022学年高一下学期期末数学试题(已下线)卷10-2020年高考数学冲刺逆袭必备卷(山东、海南专用)【学科网名师堂】江苏省镇江市扬中市第二高级中学2022-2023学年高二下学期期末模拟数学试题安徽省合肥六校联盟2022-2023学年高二下学期期末联考数学试卷重庆市杨家坪中学2022-2023学年高二上学期期末数学试题四川省南充市2023-2024学年高二上学期期末模拟数学试题(四)陕西宝鸡金台区2023-2024学年高二上学期期末质量检测数学试题(已下线)黄金卷07 【赢在高考·黄金20卷】备战2021年高考数学全真模拟卷(广东专用)广东省广大附中、铁一、广外三校2020-2021学年高二下学期期中联考数学试题湖北省武汉市蔡甸区汉阳一中2020-2021学年高一下学期5月月考数学试题福建省厦门市集美中学2020-2021学年高二下学期第一次月考数学试题北师大版(2019) 选修第一册 必杀技 第三章 素养检测广东省广州市西关外国语学校2022届高三上学期8月月考数学试题辽宁省沈阳市第八十三中学2021-2022学年高二上学期开学考试数学试题山西省太原市第五中学2021-2022学年高二上学期10月月考数学试题(已下线)考点16 空间向量与立体几何-2022年高考数学一轮复习小题多维练(新高考版)福建省三明市教研联盟校2021—2022学年高二上学期期中联考数学试题(已下线)2021年全国新高考Ⅰ卷数学试题变式题7-12题河北省衡水市武强中学2022届高三上学期第二次月考数学A卷试题(已下线)解密12 空间向量在空间几何体中应用(分层训练)-【高频考点解密】2022年高考数学二轮复习讲义+分层训练(新高考专用)江苏省镇江市扬中市第二高级中学2021-2022学年高二下学期期初数学试题(已下线)复习题三1(已下线)专题06 空间向量与立体几何(突破训练)-备战2022年高考数学二轮复习重难考点专项突破训练(全国通用)重庆市复旦中学2021-2022学年高二下学期开学考试数学试题江苏省扬州中学2021-2022学年高二下学期3月月考数学试题重庆市实验中学2021-2022学年高二上学期第二次阶段性测试数学试题(已下线)第52讲 空间向量在立体几何中的运用山东省东营市广饶县第一中学2022-2023学年高二上学期10月月考数学试题山东省枣庄市滕州市第一中学2022-2023学年高二上学期10月月考数学试题江西省南昌市新建区第二中学2022-2023学年高二上学期10月学业水平考核数学试题江苏省无锡市江阴高级中学2021-2022学年高二上学期期中数学试题河北省邯郸市魏县第五中学2022-2023学年高二上学期第二次月考数学试题福建省永安第九中学2022-2023学年高二上学期期中考试数学试题广东省揭阳市普宁市第二中学2022-2023学年高二上学期期中数学试题河南市郑州优胜实验中学2022-2023学年高二上学期10月第一次月考数学试题江西省余干中学2022-2023学年高二上学期(3—26班)第三次半月考(网课)数学试题浙江省金华市曙光学校2022-2023学年高二上学期期中数学试题(已下线)山东省济南市2022届高三二模数学试题变式题11-16(已下线)2022-2023学年高二数学同步讲与练(空间向量与立体几何、直线与圆、圆锥曲线、数列)(已下线)福建省泉州第一中学2021-2022学年高一下学期期中考试数学试题(已下线)第4讲 空间向量的应用 (2)(已下线)6.3.3空间角的计算(3)江苏省镇江中学2022-2023学年高二下学期6月月考数学试题第三章空间向量与立体几何测评--2022-2023学年高二上学期数学北师大版(2019)选择性必修第一册第三章空间向量与立体几何 章末测评卷-2022-2023学年高二上学期数学北师大版(2019)选择性必修第一册第三章空间向量与立体几何单元测试 2021-2022学年高二上学期数学北师大版(2019)选择性必修第一册(已下线)模块三 专题1 小题入门夯实练 (2)(苏教版高二)(已下线)1.4.2用空间向量研究距离、夹角问题(第2课时)辽宁省葫芦岛市东北师范大学连山实验高中2023-2024学年高二上学期10月月考数学试题四川省达州市万源市万源中学2023-2024学年高二上学期10月月考数学试题山西省大同市第三中学校2024届高三上学期十月月考数学试题河南大学附属中学2023-2024学年高二上学期8月开学考试数学试题专题07A立体几何选择填空题河北省石家庄二十二中2023-2024学年高二上学期第一次月考(10月)数学试题福建省平山中学、内坑中学、磁灶中学、永春二中、永和中学2023-2024学年高二上学期期中联考数学试题辽宁省辽西联合校2023-2024学年高二上学期期中考试数学试题安徽省芜湖市2023-2024学年高二上学期期中联考数学试题广东省肇庆市肇庆鼎湖中学2023-2024学年高二上学期期中质量检测数学试题江苏省清河中学2022-2023学年高二下学期3月阶段测试数学试卷(已下线)第六章 空间向量与立体几何(单元重点综合测试)-2023-2024学年高二数学单元速记·巧练(苏教版2019选择性必修第二册)(已下线)第二章 立体几何中的计算 专题六 空间定值问题 微点3 立体几何中的定比问题【培优版】单元测试A卷——第一章 空间向量与立体几何(已下线)空间向量与立体几何02-一轮复习考点专练【巩固卷】第2章 空间向量与立体几何素养检测 单元测试A-湘教版(2019)选择性必修第二册四川省成都市新津中学2024-2025学年高二上学期10月月考数学试题陕西省咸阳实验中学2024-2025学年高二上学期第一次阶段性测试数学试卷辽宁省抚顺市第一中学2024-2025学年高二上学期10月测试数学试题海南省琼海市琼海市嘉积中学2024-2025学年高二上学期10月月考数学试题江西省南昌市第二中学2024-2025学年高二上学期月考(一)数学试卷四川省蓬溪县蓬南中学2024-2025学年高二上学期第一次月考数学试题江西省景德镇市2024-2025学年高二上学期11月期中考试数学试题
名校
4 . 如图,在四棱锥 中,底面
中,底面 是边长为4的正方形,
是边长为4的正方形,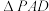 是等边三角形,
是等边三角形,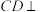 平面
平面 ,E,F,G,O分别是PC,PD,BC,AD的中点.
,E,F,G,O分别是PC,PD,BC,AD的中点. 平面
平面 ;
;
(2)求平面 与平面
与平面 的夹角的大小;
的夹角的大小;
(3)线段PA上是否存在点M,使得直线GM与平面 所成角为
所成角为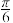 ,若存在,求线段PM的长;若不存在,说明理由.
,若存在,求线段PM的长;若不存在,说明理由.
 中,底面
中,底面 是边长为4的正方形,
是边长为4的正方形,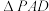 是等边三角形,
是等边三角形,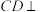 平面
平面 ,E,F,G,O分别是PC,PD,BC,AD的中点.
,E,F,G,O分别是PC,PD,BC,AD的中点.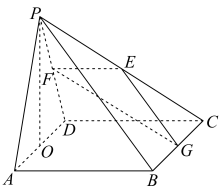
 平面
平面 ;
;(2)求平面
 与平面
与平面 的夹角的大小;
的夹角的大小;(3)线段PA上是否存在点M,使得直线GM与平面
 所成角为
所成角为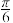 ,若存在,求线段PM的长;若不存在,说明理由.
,若存在,求线段PM的长;若不存在,说明理由.
您最近一年使用:0次
2022-04-27更新
|
2759次组卷
|
34卷引用:北京市石景山区2019-2020学年高三上学期期末考试数学试题
北京市石景山区2019-2020学年高三上学期期末考试数学试题吉林省长春市第六中学2023-2024学年高二上学期1月期末考试数学试题2020届山东省潍坊市高三2月数学模拟试题(一)(已下线)备战2020年高考数学之考场再现(山东专版)062020届山东省寿光市第二中学高三线上2月29日数学高考模拟题(三)2020届北京八中高三3月学模拟考试数学(二)试题2020届北京市第八中学高三下学期自主测试(二)数学试题山东省日照五莲县丶潍坊安丘市、潍坊诸城市、临沂兰山区2020届高三6月模拟数学试题天津市北辰区2020届高考二模数学试题(已下线)第9篇——立体几何与空间向量-新高考山东专题汇编(已下线)专题16 立体几何-2020年高考数学母题题源解密(北京专版)天津市南开中学2020-2021学年高二上学期期中数学试题北京市第十二中学2020-2021学年高二12月月考数学试题北京交通大学附属中学2021-2022学年高二上学期期末考试数学试题天津市九十六中学2022-2023学年高二上学期期末数学试题天津市河西区2021-2022学年高二上学期期中数学试题(已下线)第3讲 立体几何中的向量方法(讲)-2022年高考数学二轮复习讲练测(新教材地区专用)(已下线)类型三 立体几何与空间向量-【题型突破】备战2022年高考数学二轮基础题型+重难题型突破(新高考专用)天津市部分区2022届高三下学期质量调查(一)数学试题天津市南开区2022届高三下学期三模数学试题甘肃省张掖市临泽县第一中学2021-2022学年高二下学期期中考试数学(理)试题北京市朝阳区清华大学附属中学朝阳学校2021-2022学年高二上学期期中数学试题天津市和平区第二十中学2022-2023学年高三上学期期中数学试题广西桂林市中山中学2022-2023学年高三上学期10月月考数学试题天津市滨海新区2023届高三三模数学试题黑龙江省牡丹江市第二高级中学2023届高三上学期期中数学试题(已下线)高二上学期期中【全真模拟卷02】(人教A版2019)江苏省郑梁梅高级中学2022-2023学年高二下学期4月月考数学试题天津市蓟州区第一中学2023-2024学年高三上学期第一次学情调研数学试题江西省贵溪市实验中学2024届高三上学期新高考模拟检测(三)数学试题天津市北师大静海实验学校2023-2024学年高二上学期第三次月考数学试题四川省眉山市北外附属东坡外国语学校2023-2024学年高二下学期开学考试数学试题(已下线)第七章 应用空间向量解立体几何问题拓展 专题二 平面法向量求法及其应用 微点1 平面法向量求法及其应用(一)【培优版】天津市蓟州区第一中学2025届高三上学期第一次学情调研数学试题
名校
5 . 如图,在四棱 中,
中, 底面
底面 ,底面
,底面 为正方形,
为正方形, ,
, 分别是
分别是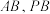 的中点.
的中点. ;
;
(2)求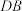 与平面
与平面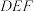 所成角的正弦值.
所成角的正弦值.
 中,
中, 底面
底面 ,底面
,底面 为正方形,
为正方形, ,
, 分别是
分别是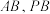 的中点.
的中点.
 ;
;(2)求
 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2022-01-04更新
|
668次组卷
|
12卷引用:吉林省辽源市田家炳高级中学友好学校2021-2022学年高二上学期期末数学试题
吉林省辽源市田家炳高级中学友好学校2021-2022学年高二上学期期末数学试题广东省江门市2017-2018学年高二上学期调研测试(一)理科数学试题湖南省醴陵市第二中学2017-2018学年高二上学期第三次月考数学(理)试题广东省江门市2018年普通高中高二调研测试(一)数学理科【全国百强校】山西大学附属中学2018-2019学年高二10月模块诊断数学试题山西省朔州市怀仁一中2018-2019学年高二(上)第四次月考数学(理科)试题(b卷)浙江省金华第一中学2021-2022学年高一领军班上学期12月联考数学试题云南省曲靖市第二中学2021-2022学年高二上学期期末数学试题(已下线)专题1.4 《空间向量与立体几何》 单元测试(B卷提升篇)-2020-2021学年高二数学选择性必修第一册同步单元AB卷(新教材人教A版,浙江专用)山东省2021-2022学年高二11月“山东学情”期中联考数学试题(B)山东省2021-2022学年高二11月“山东学情”期中联考数学试题(A)山西省大同市浑源县第七中学校2024-2025学年高二上学期第一次月考数学试题
名校
6 . 如图,三棱柱 中,侧棱
中,侧棱 平面ABC,
平面ABC, 为等腰直角三角形,
为等腰直角三角形,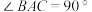 ,且
,且 ,E,F分别是
,E,F分别是 ,
, 的中点.
的中点. 的中点,求证:
的中点,求证: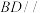 平面AEF;
平面AEF;
(Ⅱ)线段AE(包括端点)上是否存在点M,使直线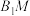 与平面AEF所成的角为
与平面AEF所成的角为 ?若有,确定点M的位置;若没有,说明理由.
?若有,确定点M的位置;若没有,说明理由.
 中,侧棱
中,侧棱 平面ABC,
平面ABC, 为等腰直角三角形,
为等腰直角三角形,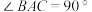 ,且
,且 ,E,F分别是
,E,F分别是 ,
, 的中点.
的中点.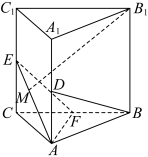
 的中点,求证:
的中点,求证: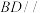 平面AEF;
平面AEF;(Ⅱ)线段AE(包括端点)上是否存在点M,使直线
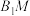 与平面AEF所成的角为
与平面AEF所成的角为 ?若有,确定点M的位置;若没有,说明理由.
?若有,确定点M的位置;若没有,说明理由.
您最近一年使用:0次
2020-12-04更新
|
1340次组卷
|
9卷引用:吉林省长春市第五中学2022-2023学年高三上学期期末数学试题
名校
解题方法
7 . 在三棱锥P-ABC中,PA,AB,AC两两垂直,D为棱PC上一动点,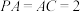 ,
, .当BD与平面PAC所成角最大时,AD与平面PBC所成角的正弦值为
.当BD与平面PAC所成角最大时,AD与平面PBC所成角的正弦值为________ .
 ,
, .当BD与平面PAC所成角最大时,AD与平面PBC所成角的正弦值为
.当BD与平面PAC所成角最大时,AD与平面PBC所成角的正弦值为
您最近一年使用:0次
2020-12-02更新
|
653次组卷
|
7卷引用:吉林省白山市2020-2021学年高二上学期期末考试数学(理科)试题
吉林省白山市2020-2021学年高二上学期期末考试数学(理科)试题河北省2020-2021学年高二上学期11月期中数学试题(已下线)第一章 空间向量与立体几何(单元测试)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第一册)(已下线)1.2.3 直线与平面的夹角(分层训练)-2023-2024学年高二数学同步精品课堂(人教B版2019选择性必修第一册)广东省梅州市大埔县虎山中学2023-2024学年高二上学期期中数学试题(已下线)1.4.2 用空间向量研究距离、夹角问题【第三课】(已下线)模块二 中等第2套 复盘卷(高二期中备考模拟)
名校
解题方法
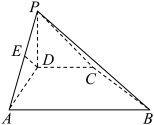
8 . 在四棱锥 中,
中, 平面
平面 ,
, ,
, ,
,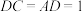 ,
, ,
, 与平面
与平面 所成的角是
所成的角是 ,
, 是
是 的中点,
的中点, 在线段
在线段 上,且满足
上,且满足 .
.
(1)求二面角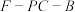 的余弦值;
的余弦值;
(2)在线段 上是否存在点
上是否存在点 ,使得
,使得 与平面
与平面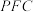 所成角的余弦值是
所成角的余弦值是 ,若存在,求
,若存在,求 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
 中,
中, 平面
平面 ,
, ,
, ,
,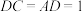 ,
, ,
, 与平面
与平面 所成的角是
所成的角是 ,
, 是
是 的中点,
的中点, 在线段
在线段 上,且满足
上,且满足 .
.
(1)求二面角
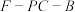 的余弦值;
的余弦值;(2)在线段
 上是否存在点
上是否存在点 ,使得
,使得 与平面
与平面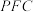 所成角的余弦值是
所成角的余弦值是 ,若存在,求
,若存在,求 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
您最近一年使用:0次
2020-03-20更新
|
348次组卷
|
2卷引用:吉林省长春市绿园区长春兴华高中2019-2020学年高二上学期期末数学(理)试题
名校
解题方法
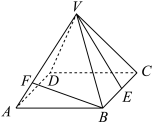
9 . 如图,在正四棱锥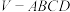 中,二面角
中,二面角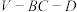 为60°,E为
为60°,E为 的中点.已知F为直线
的中点.已知F为直线 上一点,且F与A不重合,若异面直线
上一点,且F与A不重合,若异面直线 与
与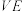 所成角为60°,则
所成角为60°,则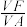 =
=_____________ .
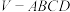 中,二面角
中,二面角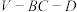 为60°,E为
为60°,E为 的中点.已知F为直线
的中点.已知F为直线 上一点,且F与A不重合,若异面直线
上一点,且F与A不重合,若异面直线 与
与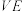 所成角为60°,则
所成角为60°,则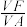 =
=
您最近一年使用:0次
2020-03-05更新
|
395次组卷
|
3卷引用:吉林省梅河口市第五中学2019-2020学年高二上学期期末数学(理)试题
10 . 如图,在直三棱柱 中,
中,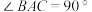 ,
,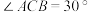 ,
,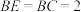 ,
, ,
, 分别是
分别是 ,
, 的中点.
的中点.

(1)证明: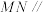 平面
平面 .
.
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,
中,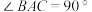 ,
,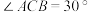 ,
,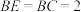 ,
, ,
, 分别是
分别是 ,
, 的中点.
的中点.
(1)证明:
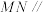 平面
平面 .
.(2)求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2020-01-17更新
|
1090次组卷
|
7卷引用:2020届吉林省通化市梅河口市第五中学高三上学期期末数学(理)试题



