名校
解题方法
1 . 已知双曲线C: (
( ,
, )的焦距为
)的焦距为 ,离心率
,离心率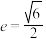 .
.
(1)求双曲线C的方程;
(2)设P,Q为双曲线C上异于点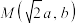 的两动点,记直线MP,MQ的斜率分别为
的两动点,记直线MP,MQ的斜率分别为 ,
, ,若
,若 ,求证:直线PQ过定点.
,求证:直线PQ过定点.
 (
( ,
, )的焦距为
)的焦距为 ,离心率
,离心率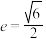 .
.(1)求双曲线C的方程;
(2)设P,Q为双曲线C上异于点
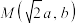 的两动点,记直线MP,MQ的斜率分别为
的两动点,记直线MP,MQ的斜率分别为 ,
, ,若
,若 ,求证:直线PQ过定点.
,求证:直线PQ过定点.
您最近一年使用:0次
2023-04-09更新
|
1151次组卷
|
6卷引用:安徽省滁州市2023届高三第二次教学质量监测数学试题
名校
解题方法
2 . 已知双曲线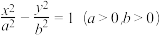 的离心率等于
的离心率等于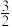 ,且点
,且点 在双曲线上.
在双曲线上.
(1)求双曲线的方程;
(2)若双曲线的左顶点为 ,右焦点为
,右焦点为 ,P为双曲线右支上任意一点,求
,P为双曲线右支上任意一点,求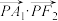 的最小值.
的最小值.
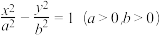 的离心率等于
的离心率等于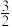 ,且点
,且点 在双曲线上.
在双曲线上.(1)求双曲线的方程;
(2)若双曲线的左顶点为
 ,右焦点为
,右焦点为 ,P为双曲线右支上任意一点,求
,P为双曲线右支上任意一点,求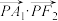 的最小值.
的最小值.
您最近一年使用:0次
2022-03-27更新
|
2065次组卷
|
16卷引用:安徽省六安市新安中学2021-2022学年高二上学期12月月考数学试题
安徽省六安市新安中学2021-2022学年高二上学期12月月考数学试题人教B版(2019) 选择性必修第一册 过关斩将 第二章 平面解析几何 2.8 直线与圆锥曲线的位置关系江苏省徐州市沛县2020-2021学年高二上学期第一次学情调研数学试题北京市平谷区第五中学2020-2021学年高二上学期期中考试数学试题(已下线)3.2.2 双曲线的简单几何性质(2)-2020-2021学年高二数学课时同步练(人教A版选择性必修第一册)(已下线)3.2.1 双曲线的标准方程(课堂培优)-2021-2022学年高二数学课后培优练(苏教版2019选择性必修第一册)(已下线)3.2.2 双曲线的几何性质(课堂培优)-2021-2022学年高二数学课后培优练(苏教版2019选择性必修第一册)人教A版(2019) 选修第一册 实战演练 第三章 课时练习25 双曲线的简单几何性质(已下线)专题3.8 双曲线的标准方程和性质-重难点题型检测-2021-2022学年高二数学举一反三系列(人教A版2019选择性必修第一册)宁夏回族自治区银川一中2022届高三二模数学(文)试题宁夏回族自治区银川一中2022届高三二模数学(理)试题(已下线)第06讲 双曲线 (精练)(已下线)第二章 平面解析几何之圆锥曲线的方程(A卷·知识通关练)(6)3.2.2 双曲线的几何性质(一)(同步练习基础版)广西玉林市博白第四高级中学2021-2022学年高二上学期期中数学(文)试题山东省威海市乳山市银滩高级中学2023-2024学年高二上学期12月月考数学试题
名校
解题方法
3 . 已知双曲线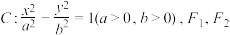 分别是
分别是 的左、右焦点.若
的左、右焦点.若 的离心率
的离心率 ,且点
,且点 在
在 上.
上.
(1)求 的方程.
的方程.
(2)若过点 的直线
的直线 与
与 的左、右两支分别交于
的左、右两支分别交于 两点(不同于双曲线的顶点),问:
两点(不同于双曲线的顶点),问: 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.
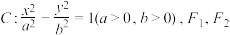 分别是
分别是 的左、右焦点.若
的左、右焦点.若 的离心率
的离心率 ,且点
,且点 在
在 上.
上.(1)求
 的方程.
的方程.(2)若过点
 的直线
的直线 与
与 的左、右两支分别交于
的左、右两支分别交于 两点(不同于双曲线的顶点),问:
两点(不同于双曲线的顶点),问: 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.
您最近一年使用:0次
2023-12-23更新
|
902次组卷
|
4卷引用:安徽省皖豫名校联盟2024届高中毕业班第二次联考数学试题
安徽省皖豫名校联盟2024届高中毕业班第二次联考数学试题黑龙江省鸡西市第一中学校2024届高三上学期期末数学试题山西省朔州市怀仁市第一中学校2023-2024学年高二上学期1月期末数学试题(已下线)专题18 圆锥曲线高频压轴解答题(16大题型)(练习)
名校
解题方法
4 . 已知双曲线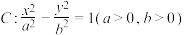 的离心率为2,且双曲线C经过点
的离心率为2,且双曲线C经过点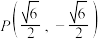 .
.
(1)求双曲线C的方程;
(2)设M是直线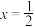 上任意一点,过点M作双曲线C的两条切线
上任意一点,过点M作双曲线C的两条切线 ,
, ,切点分别为A,B,试判断直线AB是否过定点.若经过定点,求出该定点的坐标;若不经过定点,请说明理由.
,切点分别为A,B,试判断直线AB是否过定点.若经过定点,求出该定点的坐标;若不经过定点,请说明理由.
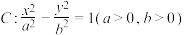 的离心率为2,且双曲线C经过点
的离心率为2,且双曲线C经过点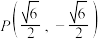 .
.(1)求双曲线C的方程;
(2)设M是直线
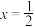 上任意一点,过点M作双曲线C的两条切线
上任意一点,过点M作双曲线C的两条切线 ,
, ,切点分别为A,B,试判断直线AB是否过定点.若经过定点,求出该定点的坐标;若不经过定点,请说明理由.
,切点分别为A,B,试判断直线AB是否过定点.若经过定点,求出该定点的坐标;若不经过定点,请说明理由.
您最近一年使用:0次
2023-04-13更新
|
766次组卷
|
5卷引用:安徽省定远中学2023届高三下学期高考冲刺卷(二)数学试卷
安徽省定远中学2023届高三下学期高考冲刺卷(二)数学试卷安徽省定远中学2023届高三下学期6月考前适应性检测数学试卷陕西省商洛市2023届高三二模文科数学试题陕西省商洛市2023届高三二模理科数学试题(已下线)河北省石家庄市2023届高三质量检测(一)数学试题变式题17-22
名校
解题方法
5 . 已知椭圆 的离心率与双曲线
的离心率与双曲线 的离心率互为倒数,且椭圆C的焦距、双曲线E的实轴长、双曲线E的焦距依次构成等比数列.
的离心率互为倒数,且椭圆C的焦距、双曲线E的实轴长、双曲线E的焦距依次构成等比数列.
(1)求椭圆C的标准方程;
(2)若双曲线E的虚轴的上端点为 ,问是否存在过点
,问是否存在过点 的直线
的直线 交椭圆C于
交椭圆C于 两点,使得以
两点,使得以 为直径的圆过原点?若存在,求出此时直线
为直径的圆过原点?若存在,求出此时直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
 的离心率与双曲线
的离心率与双曲线 的离心率互为倒数,且椭圆C的焦距、双曲线E的实轴长、双曲线E的焦距依次构成等比数列.
的离心率互为倒数,且椭圆C的焦距、双曲线E的实轴长、双曲线E的焦距依次构成等比数列.(1)求椭圆C的标准方程;
(2)若双曲线E的虚轴的上端点为
 ,问是否存在过点
,问是否存在过点 的直线
的直线 交椭圆C于
交椭圆C于 两点,使得以
两点,使得以 为直径的圆过原点?若存在,求出此时直线
为直径的圆过原点?若存在,求出此时直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
您最近一年使用:0次
2021-08-13更新
|
2422次组卷
|
8卷引用:安徽省淮南一中2020-2021学年高二下学期第二次段考理科数学试题
安徽省淮南一中2020-2021学年高二下学期第二次段考理科数学试题安徽省淮南市淮南第一中学2020-2021学年高二下学期期中数学试题(理)(已下线)专题24 圆锥曲线中的存在性、探索性问题 微点2 圆锥曲线中的探索性问题内蒙古赤峰二中2022-2023学年高二上学期第一次月考(11月)数学(文)试题上海市华东师范大学第三附属中学2021-2022学年高二下学期3月月考数学试题(已下线)高二下学期第一次月考卷(测试范围:沪教版2020选修一前两章)内蒙古赤峰二中2022-2023学年高二下学期第二次月考数学(文)试题四川省成都市石室中学2023届高三适应性模拟检测理科数学试题
6 . 已知双曲线C: 的离心率为2.且经过点
的离心率为2.且经过点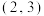 .
.
(1)求C的方程;
(2)若直线l与C交于A,B两点,且 (点O为坐标原点),求
(点O为坐标原点),求 的取值范围.
的取值范围.
 的离心率为2.且经过点
的离心率为2.且经过点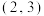 .
.(1)求C的方程;
(2)若直线l与C交于A,B两点,且
 (点O为坐标原点),求
(点O为坐标原点),求 的取值范围.
的取值范围.
您最近一年使用:0次
解题方法
7 . 已知双曲线 与椭圆
与椭圆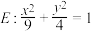 的焦点重合,且
的焦点重合,且 与
与 的离心率之积为
的离心率之积为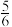 .
.
(1)求双曲线 的标准方程;
的标准方程;
(2)设双曲线 的左、右顶点分别为
的左、右顶点分别为 ,若直线
,若直线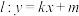 与圆
与圆 相切,且与双曲线左、右两支分别交于
相切,且与双曲线左、右两支分别交于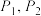 两点,记直线
两点,记直线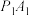 的斜率为
的斜率为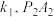 的斜率为
的斜率为 ,那么
,那么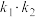 是否为定值?并说明理由.
是否为定值?并说明理由.
 与椭圆
与椭圆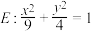 的焦点重合,且
的焦点重合,且 与
与 的离心率之积为
的离心率之积为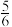 .
.(1)求双曲线
 的标准方程;
的标准方程;(2)设双曲线
 的左、右顶点分别为
的左、右顶点分别为 ,若直线
,若直线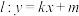 与圆
与圆 相切,且与双曲线左、右两支分别交于
相切,且与双曲线左、右两支分别交于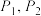 两点,记直线
两点,记直线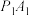 的斜率为
的斜率为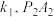 的斜率为
的斜率为 ,那么
,那么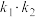 是否为定值?并说明理由.
是否为定值?并说明理由.
您最近一年使用:0次
2023-08-08更新
|
485次组卷
|
4卷引用:安徽省滁州市全椒县第八中学2022-2023学年高二下学期5月联考数学试题
安徽省滁州市全椒县第八中学2022-2023学年高二下学期5月联考数学试题安徽省滁州市明光市第二中学2022-2023学年高二下学期第一次月考数学试卷(已下线)2.2.1 双曲线及其标准方程(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)(已下线)第3章 圆锥曲线与方程章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第一册)
名校
解题方法
8 . 已知 是双曲线
是双曲线 上相异的三个点,点
上相异的三个点,点 关于原点对称,直线
关于原点对称,直线 的斜率乘积为2.
的斜率乘积为2.
(1)求双曲线 的离心率.
的离心率.
(2)若双曲线 过点
过点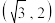 ,过圆
,过圆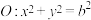 上一点
上一点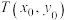 作圆
作圆 的切线
的切线 ,直线
,直线 交双曲线
交双曲线 于
于 两点,
两点,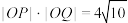 ,求直线
,求直线 的方程.
的方程.
 是双曲线
是双曲线 上相异的三个点,点
上相异的三个点,点 关于原点对称,直线
关于原点对称,直线 的斜率乘积为2.
的斜率乘积为2.(1)求双曲线
 的离心率.
的离心率.(2)若双曲线
 过点
过点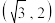 ,过圆
,过圆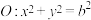 上一点
上一点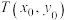 作圆
作圆 的切线
的切线 ,直线
,直线 交双曲线
交双曲线 于
于 两点,
两点,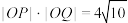 ,求直线
,求直线 的方程.
的方程.
您最近一年使用:0次
2023-02-10更新
|
481次组卷
|
2卷引用:安徽省舒城中学2023届仿真模拟卷(一)数学试题
名校
解题方法
9 . 已知双曲线 的左、右焦点分别为
的左、右焦点分别为 ,离心率为
,离心率为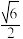 ,直线
,直线 交
交 于
于 两点,且
两点,且 .
.
(1)求双曲线 的标准方程;
的标准方程;
(2)若点 ,直线
,直线 与
与 轴分别相交于
轴分别相交于 两点,且
两点,且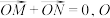 为坐标原点,证明:直线
为坐标原点,证明:直线 过定点.
过定点.
 的左、右焦点分别为
的左、右焦点分别为 ,离心率为
,离心率为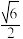 ,直线
,直线 交
交 于
于 两点,且
两点,且 .
.(1)求双曲线
 的标准方程;
的标准方程;(2)若点
 ,直线
,直线 与
与 轴分别相交于
轴分别相交于 两点,且
两点,且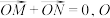 为坐标原点,证明:直线
为坐标原点,证明:直线 过定点.
过定点.
您最近一年使用:0次
2022-12-22更新
|
801次组卷
|
4卷引用:安徽省部分学校2022-2023学年高三上学期12月联考数学试题
解题方法
10 . 已知O为坐标原点, 分别是双曲线
分别是双曲线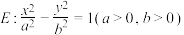 的左、右焦点,直线
的左、右焦点,直线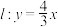 与E交于A,B两点,
与E交于A,B两点,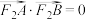 ﹒
﹒
(1)求E的离心率;
(2)M为E上一点(不在x轴上),过 作
作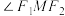 平分线的垂线,垂足为N,若
平分线的垂线,垂足为N,若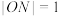 ,求
,求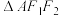 的面积.
的面积.
 分别是双曲线
分别是双曲线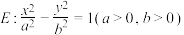 的左、右焦点,直线
的左、右焦点,直线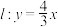 与E交于A,B两点,
与E交于A,B两点,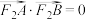 ﹒
﹒(1)求E的离心率;
(2)M为E上一点(不在x轴上),过
 作
作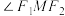 平分线的垂线,垂足为N,若
平分线的垂线,垂足为N,若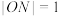 ,求
,求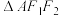 的面积.
的面积.
您最近一年使用:0次



