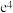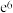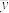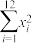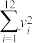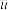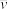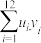名校
解题方法
1 . 随着科技发展的日新月异,人工智能融入了各个行业,促进了社会的快速发展.其中利用人工智能生成的虚拟角色因为拥有更低的人工成本,正逐步取代传统的真人直播带货.某公司使用虚拟角色直播带货销售金额得到逐步提升,以下为该公司自2023年8月使用虚拟角色直播带货后的销售金额情况统计.
若 与
与 的相关关系拟用线性回归模型表示,回答如下问题:
的相关关系拟用线性回归模型表示,回答如下问题:
(1)试求变量 与
与 的样本相关系数
的样本相关系数 (结果精确到0.01);
(结果精确到0.01);
(2)试求 关于
关于 的经验回归方程,并据此预测2024年2月份该公司的销售金额.(
的经验回归方程,并据此预测2024年2月份该公司的销售金额.(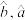 ,均保留一位小数)
,均保留一位小数)
附:经验回归方程 ,其中
,其中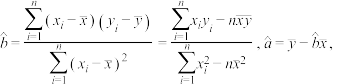 ,
,
样本相关系数
参考数据: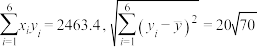 .
.
年月 | 2023年8月 | 2023年9月 | 2023年10月 | 2023年11月 | 2023年12月 | 2024年1月 |
月份编号 | 1 | 2 | 3 | 4 | 5 | 6 |
销售金额 | 15.4 | 25.4 | 35.4 | 85.4 | 155.4 | 195.4 |
 与
与 的相关关系拟用线性回归模型表示,回答如下问题:
的相关关系拟用线性回归模型表示,回答如下问题:(1)试求变量
 与
与 的样本相关系数
的样本相关系数 (结果精确到0.01);
(结果精确到0.01);(2)试求
 关于
关于 的经验回归方程,并据此预测2024年2月份该公司的销售金额.(
的经验回归方程,并据此预测2024年2月份该公司的销售金额.(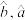 ,均保留一位小数)
,均保留一位小数)附:经验回归方程
 ,其中
,其中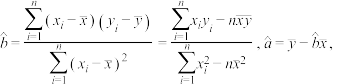 ,
,样本相关系数

参考数据:
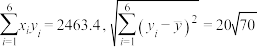 .
.
您最近半年使用:0次
今日更新
|
216次组卷
|
12卷引用:河南省名校联考2023-2024学年高二下学期4月月考数学试题
河南省名校联考2023-2024学年高二下学期4月月考数学试题(已下线)第八章 成对数据的统计分析(知识归纳+题型突破)-2023-2024学年高二数学单元速记·巧练(沪教版2020选择性必修第二册)(已下线)8.2 一元线性回归模型及其应用(分层练习,7大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)9.1 线性回归分析(2)(已下线)8.2 一元线性回归模型及其应用——课后作业(巩固版)湖北省武汉市2024届高中毕业班二月调研考试数学试题山东省菏泽第一中学八一路校区2024届高三下学期开学考试数学试题(已下线)热点8-2 概率与统计综合(10题型+满分技巧+限时检测)(已下线)专题08 统计案例分析(讲义)(已下线)【一题多变】 相关关系 回归分析(已下线)专题10.1 概率与统计的综合运用【十一大题型】(举一反三)(新高考专用)-2河北省保定市高碑店市崇德实验中学2024届高三下学期3月月考数学试题
解题方法
2 . 某城市理论预测2015年到2019年人口总数与年份的关系如下表所示
(1)请用相关系数说明该组数据中 与
与 之间的关系可用线性回归模型进行拟合;
之间的关系可用线性回归模型进行拟合;
(2)求出 关于
关于 的线性回归方程
的线性回归方程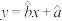 ;
;
(3)据此估计2021年该城市人口总数.
参考公式:相关系数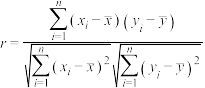 ,对于一组具有线性相关关系的数据
,对于一组具有线性相关关系的数据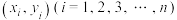 ,其回归直线
,其回归直线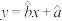 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
时间代号 | 0 | 1 | 2 | 3 | 4 |
人口总数(十万) | 5 | 7 | 8 | 11 | 19 |
 与
与 之间的关系可用线性回归模型进行拟合;
之间的关系可用线性回归模型进行拟合;(2)求出
 关于
关于 的线性回归方程
的线性回归方程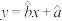 ;
;(3)据此估计2021年该城市人口总数.
参考公式:相关系数
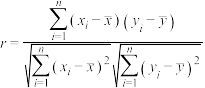 ,对于一组具有线性相关关系的数据
,对于一组具有线性相关关系的数据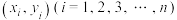 ,其回归直线
,其回归直线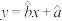 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
您最近半年使用:0次
3 . 已知变量y关于x的回归方程为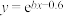 ,若对
,若对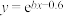 两边取自然对数,可以发现
两边取自然对数,可以发现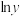 与x线性相关,现有一组数据如下表所示:
与x线性相关,现有一组数据如下表所示:
则当 时,预测y的值为
时,预测y的值为____________ .
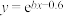 ,若对
,若对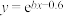 两边取自然对数,可以发现
两边取自然对数,可以发现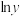 与x线性相关,现有一组数据如下表所示:
与x线性相关,现有一组数据如下表所示:x | 1 | 2 | 3 | 4 | 5 |
y |
|
|
|
|
|
 时,预测y的值为
时,预测y的值为
您最近半年使用:0次
名校
解题方法
4 . 某运动服饰公司对产品研发的年投资额 (单位:十万元)与年销售量
(单位:十万元)与年销售量 (单位:万件)的数据进行统计,整理后得到如下统计表:
(单位:万件)的数据进行统计,整理后得到如下统计表:
(1)求 和
和 的样本相关系数
的样本相关系数 (精确到0.01),并推断
(精确到0.01),并推断 和
和 的线性相关程度;(若
的线性相关程度;(若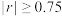 ,则线性相关程度很强;若
,则线性相关程度很强;若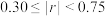 ,则线性相关程度一般;若
,则线性相关程度一般;若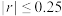 ,则线性相关程度很弱)
,则线性相关程度很弱)
(2)求年销售量 关于年投资额
关于年投资额 的回归直线方程,并据此预测年投资额为60万元时的年销售量.
的回归直线方程,并据此预测年投资额为60万元时的年销售量.
参考数据: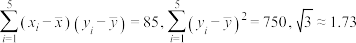 .
.
参考公式:相关系数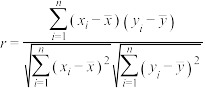 ;
;
回归直线方程 中,
中,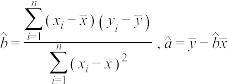 .
.
 (单位:十万元)与年销售量
(单位:十万元)与年销售量 (单位:万件)的数据进行统计,整理后得到如下统计表:
(单位:万件)的数据进行统计,整理后得到如下统计表:
| 1 | 2 | 3 | 4 | 5 |
| 35 | 40 | 50 | 55 | 70 |
 和
和 的样本相关系数
的样本相关系数 (精确到0.01),并推断
(精确到0.01),并推断 和
和 的线性相关程度;(若
的线性相关程度;(若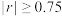 ,则线性相关程度很强;若
,则线性相关程度很强;若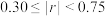 ,则线性相关程度一般;若
,则线性相关程度一般;若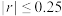 ,则线性相关程度很弱)
,则线性相关程度很弱)(2)求年销售量
 关于年投资额
关于年投资额 的回归直线方程,并据此预测年投资额为60万元时的年销售量.
的回归直线方程,并据此预测年投资额为60万元时的年销售量.参考数据:
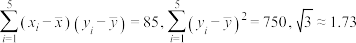 .
.参考公式:相关系数
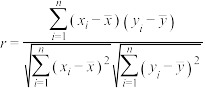 ;
;回归直线方程
 中,
中,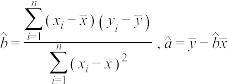 .
.
您最近半年使用:0次
解题方法
5 . 国内某企业研发了一款产品,根据产品成本,每件产品售价不低于43元,经调研,产品售价 (单位:元/件)与月销售量
(单位:元/件)与月销售量 (单位:万件),并得到随机变量
(单位:万件),并得到随机变量 相对应的一组数据为
相对应的一组数据为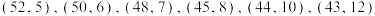 .
.
(1)根据相关系数 (结果保留两位小数),判断是否可以用线性回归模型拟合
(结果保留两位小数),判断是否可以用线性回归模型拟合 与
与 的关系,当
的关系,当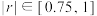 时,可以认为两个变量有很强的线性相关性;否则,没有很强的线性相关性.(参考数据:
时,可以认为两个变量有很强的线性相关性;否则,没有很强的线性相关性.(参考数据: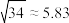 )
)
(2)建立 关于
关于 的经验回归方程,并估计当产品的月销售量86875件时,该产品的售价约为多少?
的经验回归方程,并估计当产品的月销售量86875件时,该产品的售价约为多少?
参考公式:相关系数 回归方程
回归方程 中斜率和截距的最小
中斜率和截距的最小
二乘估计公式分别为: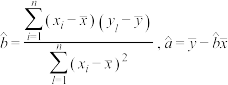 .
.
 (单位:元/件)与月销售量
(单位:元/件)与月销售量 (单位:万件),并得到随机变量
(单位:万件),并得到随机变量 相对应的一组数据为
相对应的一组数据为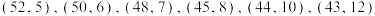 .
.(1)根据相关系数
 (结果保留两位小数),判断是否可以用线性回归模型拟合
(结果保留两位小数),判断是否可以用线性回归模型拟合 与
与 的关系,当
的关系,当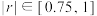 时,可以认为两个变量有很强的线性相关性;否则,没有很强的线性相关性.(参考数据:
时,可以认为两个变量有很强的线性相关性;否则,没有很强的线性相关性.(参考数据: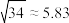 )
)(2)建立
 关于
关于 的经验回归方程,并估计当产品的月销售量86875件时,该产品的售价约为多少?
的经验回归方程,并估计当产品的月销售量86875件时,该产品的售价约为多少?参考公式:相关系数
 回归方程
回归方程 中斜率和截距的最小
中斜率和截距的最小二乘估计公式分别为:
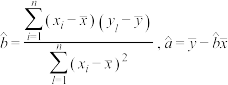 .
.
您最近半年使用:0次
解题方法
6 . 环境监测部门为调研汽车流量对空气质量的影响,在某监测点统计每日过往的汽车流量 (单位:辆)和空气中的PM2.5的平均浓度
(单位:辆)和空气中的PM2.5的平均浓度 (单位:
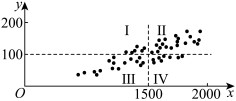
(单位: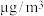 ).调研人员采集了50天的数据,制作了关于
).调研人员采集了50天的数据,制作了关于 的散点图,并用直线
的散点图,并用直线 与
与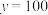 将散点图分成如图所示的四个区域I,II,III,IV,落入对应区域的样本点的个数依次为
将散点图分成如图所示的四个区域I,II,III,IV,落入对应区域的样本点的个数依次为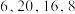 .
. 列联表,并判断至少有多大把握认为“PM2.5平均浓度不小于
列联表,并判断至少有多大把握认为“PM2.5平均浓度不小于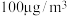 ”与“汽车日流量不小于1500辆”有关;
”与“汽车日流量不小于1500辆”有关;
(2)经计算得到回归方程为 ,且这50天的汽车日流量
,且这50天的汽车日流量 的标准差
的标准差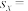 252,PM2.5的平均浓度
252,PM2.5的平均浓度 的标准差
的标准差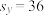 ,求相关系数
,求相关系数 ,并判断该回归方程是否有价值.
,并判断该回归方程是否有价值.
参考公式: ,其中
,其中 .
.
回归方程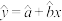 ,其中
,其中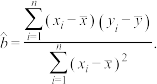 .
.
相关系数 .若
.若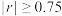 ,则认为
,则认为 与
与 有较强的线性相关性.
有较强的线性相关性.
 (单位:辆)和空气中的PM2.5的平均浓度
(单位:辆)和空气中的PM2.5的平均浓度 (单位:
(单位: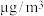 ).调研人员采集了50天的数据,制作了关于
).调研人员采集了50天的数据,制作了关于 的散点图,并用直线
的散点图,并用直线 与
与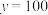 将散点图分成如图所示的四个区域I,II,III,IV,落入对应区域的样本点的个数依次为
将散点图分成如图所示的四个区域I,II,III,IV,落入对应区域的样本点的个数依次为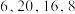 .
.
 列联表,并判断至少有多大把握认为“PM2.5平均浓度不小于
列联表,并判断至少有多大把握认为“PM2.5平均浓度不小于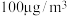 ”与“汽车日流量不小于1500辆”有关;
”与“汽车日流量不小于1500辆”有关;汽车日流量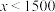 | 汽车日流量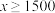 | 合计 | |
PM2.5的平均浓度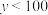 | |||
PM2.5的平均浓度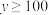 | |||
| 合计 |
(2)经计算得到回归方程为
 ,且这50天的汽车日流量
,且这50天的汽车日流量 的标准差
的标准差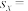 252,PM2.5的平均浓度
252,PM2.5的平均浓度 的标准差
的标准差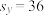 ,求相关系数
,求相关系数 ,并判断该回归方程是否有价值.
,并判断该回归方程是否有价值.参考公式:
 ,其中
,其中 .
. | 0.100 | 0.050 | 0.010 | 0.001 |
 | 2.706 | 3.841 | 6.635 | 10.828 |
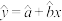 ,其中
,其中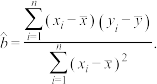 .
.相关系数
 .若
.若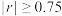 ,则认为
,则认为 与
与 有较强的线性相关性.
有较强的线性相关性.
您最近半年使用:0次
7 . ①线性回归方程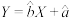 必过
必过 ;②独立性检验的统计假设是各事件之间相互独立③相关系数
;②独立性检验的统计假设是各事件之间相互独立③相关系数 越小,表明两个变量相关性越弱;④在一个
越小,表明两个变量相关性越弱;④在一个 列联表中,由计算得
列联表中,由计算得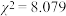 ,则有
,则有 的把握认为这两个变量间有关系;其中正确的说法是
的把握认为这两个变量间有关系;其中正确的说法是___________ .(把你认为正确的结论都写在横线上)
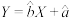 必过
必过 ;②独立性检验的统计假设是各事件之间相互独立③相关系数
;②独立性检验的统计假设是各事件之间相互独立③相关系数 越小,表明两个变量相关性越弱;④在一个
越小,表明两个变量相关性越弱;④在一个 列联表中,由计算得
列联表中,由计算得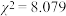 ,则有
,则有 的把握认为这两个变量间有关系;其中正确的说法是
的把握认为这两个变量间有关系;其中正确的说法是
您最近半年使用:0次
解题方法
8 . 某民营学校为增强实力与影响力,大力招揽名师、建设校园硬件设施,近5年该校招生人数的数据如下表:
(1)由表中数据可看出,可用线性回归模型拟合 与
与 的关系,请用相关系数加以证明;
的关系,请用相关系数加以证明;
(2)求 关于
关于 的回归直线方程,并预测当年份序号为7时该校的招生人数.
的回归直线方程,并预测当年份序号为7时该校的招生人数.
参考数据: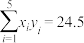 ,
, ,
, .
.
参考公式:相关系数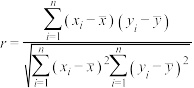 ,回归方程
,回归方程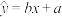 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为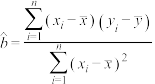 ,
, .
.
年份序号x | 1 | 2 | 3 | 4 | 5 |
招生人数y/千人 | 0.8 | 1 | 1.3 | 1.7 | 2.2 |
 与
与 的关系,请用相关系数加以证明;
的关系,请用相关系数加以证明;(2)求
 关于
关于 的回归直线方程,并预测当年份序号为7时该校的招生人数.
的回归直线方程,并预测当年份序号为7时该校的招生人数.参考数据:
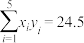 ,
, ,
, .
.参考公式:相关系数
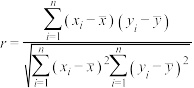 ,回归方程
,回归方程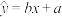 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为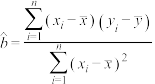 ,
, .
.
您最近半年使用:0次
2024-04-07更新
|
763次组卷
|
2卷引用:河南省南阳市华龙高级中学2023-2024学年高二下学期3月月考数学试题
解题方法
9 . 某公司为了解年研发资金投入量 (单位:亿元)对年销售额
(单位:亿元)对年销售额 (单位:亿元)的影响,对公司近12年的年研发资金投入量
(单位:亿元)的影响,对公司近12年的年研发资金投入量 和年销售额
和年销售额 的数据,进行了对比分析,建立了①
的数据,进行了对比分析,建立了①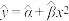 ,②
,② 两个模型,其中
两个模型,其中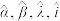 均为常数,
均为常数, 为自然对数的底数,并得到一些统计量的值.令
为自然对数的底数,并得到一些统计量的值.令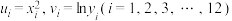 ,经计算得到如下数据:
,经计算得到如下数据:
(1)请从相关系数的角度,分析哪一个模型的拟合程度更好;
(2)由(1)的结论,求拟合程度更好的线性回归方程;
(3)若该公司计划年销售额突破10亿元,根据以上所求的线性回归方程,预测该公司年研发资金投入量至少为多少亿元.
附:相关系数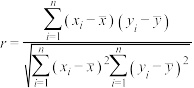 .
.
线性回归方程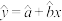 中,
中,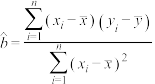 ,
,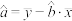 .
.
取 .
.
 (单位:亿元)对年销售额
(单位:亿元)对年销售额 (单位:亿元)的影响,对公司近12年的年研发资金投入量
(单位:亿元)的影响,对公司近12年的年研发资金投入量 和年销售额
和年销售额 的数据,进行了对比分析,建立了①
的数据,进行了对比分析,建立了①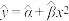 ,②
,② 两个模型,其中
两个模型,其中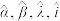 均为常数,
均为常数, 为自然对数的底数,并得到一些统计量的值.令
为自然对数的底数,并得到一些统计量的值.令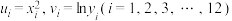 ,经计算得到如下数据:
,经计算得到如下数据:
|
| | |
|
| |||
22 | 66 | 5885 | 52276 | 460 | 5 | |||
| |
| | |||||
31250 | 364540 | 3.08 | 1334 | |||||
(2)由(1)的结论,求拟合程度更好的线性回归方程;
(3)若该公司计划年销售额突破10亿元,根据以上所求的线性回归方程,预测该公司年研发资金投入量至少为多少亿元.
附:相关系数
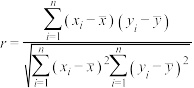 .
.线性回归方程
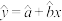 中,
中,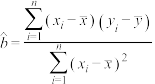 ,
,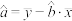 .
.取
 .
.
您最近半年使用:0次
名校
解题方法
10 . 如图是我国2016年至2022年生活垃圾无害化处理量(单位:亿吨)的折线图.
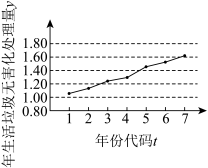
注:年份代码1-7分别对应年份2016-2022.
(1)由折线图看出,可用线性回归模型拟合 与
与 的关系,请用相关系数(精确到0.01)加以说明;
的关系,请用相关系数(精确到0.01)加以说明;
(2)建立 关于
关于 的回归方程(
的回归方程( 精确到0.01),预测2024年我国生活垃圾无害化处理量.
精确到0.01),预测2024年我国生活垃圾无害化处理量.
附注:参考数据: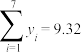 ,
,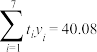 ,
,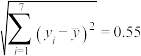 ,
,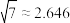 .
.
参考公式:相关系数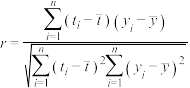 ,回归方程
,回归方程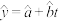 中斜率和截距最小二乘估计公式分别为
中斜率和截距最小二乘估计公式分别为 ,
,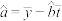 .
.

注:年份代码1-7分别对应年份2016-2022.
(1)由折线图看出,可用线性回归模型拟合
 与
与 的关系,请用相关系数(精确到0.01)加以说明;
的关系,请用相关系数(精确到0.01)加以说明;(2)建立
 关于
关于 的回归方程(
的回归方程( 精确到0.01),预测2024年我国生活垃圾无害化处理量.
精确到0.01),预测2024年我国生活垃圾无害化处理量.附注:参考数据:
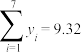 ,
,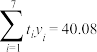 ,
,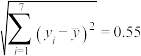 ,
,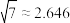 .
.参考公式:相关系数
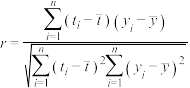 ,回归方程
,回归方程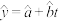 中斜率和截距最小二乘估计公式分别为
中斜率和截距最小二乘估计公式分别为 ,
,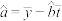 .
.
您最近半年使用:0次