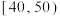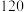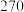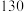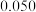1 . 某同学做立定投篮训练,共做3组,每组投篮次数和命中的次数如下表:
根据表中的数据信息,用频率估计一次投篮命中的概率,则使误差较小、可能性大的估计值是( )
第一组 | 第二组 | 第三组 | 合计 | |
投篮次数 | 100 | 200 | 300 | 600 |
命中的次数 | 68 | 124 | 174 | 366 |
命中的频率 | 0.68 | 0.62 | 0.58 | 0.61 |
| A.0.58 | B.0.61 | C.0.62 | D.0.68 |
您最近半年使用:0次
2023-07-03更新
|
179次组卷
|
3卷引用:山西省三重教育2022-2023学年高一下学期期末数学试题
名校
解题方法
2 . 某公司有员工140人,为调查员工对薪酬待遇的满意度,现随机抽取了15人,通过问卷调查,有3人对薪酬不满意.
(1)试估计公司中对薪酬不满意的人数;
(2)从15名调查对象中抽取2人,用 表示其中对薪酬不满意的人数,试求
表示其中对薪酬不满意的人数,试求 的数学期望
的数学期望 ;
;
(3)实际上,由于问题比较敏感,被调查者为了保护自己的隐私往往会做出相反的回答,导致调查数据失真.为此对调查方法进行优化,现向15名调查对象提供两个问题:
问题A:你对公司薪酬是否不满意?
问题B:现场抛一枚硬币,是否正面朝上?
在一个密闭房间里有一个箱子,箱子中放入大小相同的10个小球,其中黑色小球7个,白色小球3个,每位调查对象进入房间后,从箱子中摸出一个小球后放回,若是黑球,则回答问题A,若是白球,则抛硬币完成问题B.若有6人回答“是”,试用全概率公式估计公司中对薪酬不满意的人数.
(1)试估计公司中对薪酬不满意的人数;
(2)从15名调查对象中抽取2人,用
 表示其中对薪酬不满意的人数,试求
表示其中对薪酬不满意的人数,试求 的数学期望
的数学期望 ;
;(3)实际上,由于问题比较敏感,被调查者为了保护自己的隐私往往会做出相反的回答,导致调查数据失真.为此对调查方法进行优化,现向15名调查对象提供两个问题:
问题A:你对公司薪酬是否不满意?
问题B:现场抛一枚硬币,是否正面朝上?
在一个密闭房间里有一个箱子,箱子中放入大小相同的10个小球,其中黑色小球7个,白色小球3个,每位调查对象进入房间后,从箱子中摸出一个小球后放回,若是黑球,则回答问题A,若是白球,则抛硬币完成问题B.若有6人回答“是”,试用全概率公式估计公司中对薪酬不满意的人数.
您最近半年使用:0次
2023-05-01更新
|
1054次组卷
|
3卷引用:山西省运城市康杰中学2022-2023学年高二下学期第二次月考数学试题
山西省运城市康杰中学2022-2023学年高二下学期第二次月考数学试题湖南省长沙市长郡中学、河南省郑州外国语学校 、浙江省杭州第二中学2023届高三二模联考数学试题(已下线)重难点突破01 概率与统计的综合应用(十八大题型)-3
解题方法
3 . 对某地区过去20年的年降水量(单位:毫米)进行统计,得到以下数据:

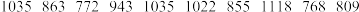
将年降水量处于799毫米及以下、800至999毫米、1000毫米及以上分别指定为降水量偏少、适中、偏多三个等级.
(1)将年降水量处于各等级的频率作为概率,分别计算该地区年降水量偏少、适中、偏多的概率;
(2)根据经验,种植甲、乙、丙三种农作物在年降水量偏少、适中、偏多的情况下可产出的年利润(单位:千元/亩)如下表所示.你认为这三种作物中,哪一种最适合在该地区推广种植?请说明理由.

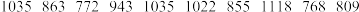
将年降水量处于799毫米及以下、800至999毫米、1000毫米及以上分别指定为降水量偏少、适中、偏多三个等级.
(1)将年降水量处于各等级的频率作为概率,分别计算该地区年降水量偏少、适中、偏多的概率;
(2)根据经验,种植甲、乙、丙三种农作物在年降水量偏少、适中、偏多的情况下可产出的年利润(单位:千元/亩)如下表所示.你认为这三种作物中,哪一种最适合在该地区推广种植?请说明理由.
年降水量 作物种类 | 偏少 | 适中 | 偏多 |
| 甲 | 8 | 12 | 8 |
| 乙 | 12 | 10 | 7 |
| 丙 | 7 | 10 | 12 |
您最近半年使用:0次
2023-04-20更新
|
302次组卷
|
6卷引用:山西省2022-2023学年高二下学期期中数学试题
山西省2022-2023学年高二下学期期中数学试题山西省晋中市2022-2023学年高二下学期期中数学试题(已下线)模块三 专题7 随机变量及其分布列--基础夯实练)(人教A版)(已下线)2023年北京高考数学真题变式题16-21(已下线)模块三 专题6 概率--(基础夯实练)(苏教版高二)(已下线)模块三 专题5 概率--大题分类练--基础夯实练(北师大2019版 高二)
4 . 某超市计划按月订购一种冷饮,根据往年销售经验,每天需求量与当天最高气温(单位: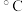 )有关.如果最高气温不低于
)有关.如果最高气温不低于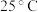 ,需求量为600瓶;如果最高气温位于区间
,需求量为600瓶;如果最高气温位于区间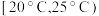 内,需求量为300瓶;如果最高气温低于
内,需求量为300瓶;如果最高气温低于 ,需求量为100瓶.为了确定6月份的订购计划,统计了前三年6月份各天的最高气温数据,得到下面的频数分布表:
,需求量为100瓶.为了确定6月份的订购计划,统计了前三年6月份各天的最高气温数据,得到下面的频数分布表:
将最高气温位于各区间的频率视为最高气温位于该区间的概率,若6月份这种冷饮一天的需求量不超过x瓶的概率估计值为0.1,则 ( )
( )
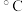 )有关.如果最高气温不低于
)有关.如果最高气温不低于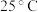 ,需求量为600瓶;如果最高气温位于区间
,需求量为600瓶;如果最高气温位于区间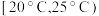 内,需求量为300瓶;如果最高气温低于
内,需求量为300瓶;如果最高气温低于 ,需求量为100瓶.为了确定6月份的订购计划,统计了前三年6月份各天的最高气温数据,得到下面的频数分布表:
,需求量为100瓶.为了确定6月份的订购计划,统计了前三年6月份各天的最高气温数据,得到下面的频数分布表:| 最高气温 | 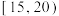 | 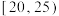 | 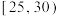 | 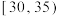 |  |
| 天数 | 3 | 6 | 25 | 38 | 18 |
 ( )
( )| A.100 | B.300 | C.400 | D.600 |
您最近半年使用:0次
2023-02-04更新
|
224次组卷
|
4卷引用:山西省晋中市2020-2021学年高三下学期4月月考理科数学试题
山西省晋中市2020-2021学年高三下学期4月月考理科数学试题天一大联考2021届高三阶段性测试(六)理科数学试题(已下线)重难专攻(十三) 概率与统计的综合问题(核心考点集训)(已下线)3频率与概率-同步精品课堂(北师大版2019必修第一册)
名校
5 . 某工厂两条生产线分别生产甲、乙两种元件,元件质量按测试指标划分为:指标大于或等于76为正品,小于76为次品.现分别从两条生产线随机抽取元件甲和元件乙各100件进行检测,检测结果统计如下:
(1)试分别估计生产一件元件甲、一件元件乙为正品的概率;
(2)生产一件元件甲,若是正品则盈利90元,若是次品则亏损10元;生产一件元件乙,若是正品则盈利100元,若是次品则亏损20元,则在(1)的前提下:
①求生产5件元件乙所获得的利润不少于300的概率;
②记X,Y分别为生产1000件元件甲和1000件元件乙所得的总利润,试比较 和
和 的大小.(结论不要求证明)
的大小.(结论不要求证明)
| 测试指标 | 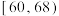 |  |  | 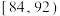 | 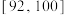 |
| 元件甲 | 12 | 8 | 40 | 33 | 7 |
| 元件乙 | 17 | 8 | 40 | 28 | 7 |
(2)生产一件元件甲,若是正品则盈利90元,若是次品则亏损10元;生产一件元件乙,若是正品则盈利100元,若是次品则亏损20元,则在(1)的前提下:
①求生产5件元件乙所获得的利润不少于300的概率;
②记X,Y分别为生产1000件元件甲和1000件元件乙所得的总利润,试比较
 和
和 的大小.(结论不要求证明)
的大小.(结论不要求证明)
您最近半年使用:0次
2022-09-11更新
|
532次组卷
|
3卷引用:山西省大同市实验中学2023届高三上学期高考考前模拟(二)数学试题
6 . 已知小张每次射击命中十环的概率都为40%,现采用随机模拟的方法估计小张三次射击恰有两次命中十环的概率,先由计算器产生0到9之间取整数值的随机数,指定2,4,6,8表示命中十环,0,1,3,5,7,9表示未命中十环,再以每三个随机数为一组,代表三次射击的结果,经随机模拟产生了如下20组随机数: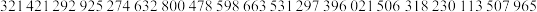 据此估计,小张三次射击恰有两次命中十环的概率约为
据此估计,小张三次射击恰有两次命中十环的概率约为__________ .
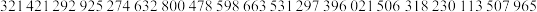 据此估计,小张三次射击恰有两次命中十环的概率约为
据此估计,小张三次射击恰有两次命中十环的概率约为
您最近半年使用:0次
2022-07-17更新
|
1208次组卷
|
8卷引用:山西省晋中市平遥县第二中学校2021-2022学年高一下学期期末数学试题
山西省晋中市平遥县第二中学校2021-2022学年高一下学期期末数学试题(已下线)第04讲 随机事件、频率与概率 (精讲)第五章 统计与概率(A卷·基础通关练)-【单元测试】2022-2023学年高一数学分层训练AB卷(人教B版2019必修第二册)(已下线)10.3频率与概率(10.3.1 频率的稳定性+10.3.2 随机模拟) (精讲)-【精讲精练】2022-2023学年高一数学下学期同步精讲精练(人教A版2019必修第二册)(已下线)第44讲 频率与概率(1)(已下线)第42讲 相互独立事件及频率与概率-【同步题型讲义】(已下线)第04讲 随机事件、频率与概率(六大题型)(讲义)(已下线)10.3.1&10.3.2?频率的稳定性、随机模拟——课后作业(提升版)
解题方法
7 . 为减少水资源的浪费,某市政府计划对居民生活用水费用实施阶梯式水价制度.为了确定一个较为合理的用水标准,有关部门通过随机抽样调查的方式,获得过去一年4000户居民的月均用水量数据(单位:吨),并根据获得的数据制作了频率分布表:
(1)求 ,
, ,
, ,
, 的值;
的值;
(2)求所获得数据中“月均用水量不低于30吨”发生的频率;
(3)若在第4,5,6组用按比例分配的分层抽样的方法随机抽取6户做问卷调查,并在这6户中任选2户进行座谈会,求这2户中恰有1户是“月均用水量不低于50吨”的概率.
组号 | 分组 | 频数 | 频率 |
|
1 |
| 1240 | 0.31 | 0.031 |
2 |
|
|
| 0.046 |
3 |
| 776 | 0.194 | 0.0194 |
4 |
| 72 | 0.018 |
|
5 |
| 48 | 0.012 | 0.0012 |
6 |
|
| 0.006 | 0.0006 |
 ,
, ,
, ,
, 的值;
的值;(2)求所获得数据中“月均用水量不低于30吨”发生的频率;
(3)若在第4,5,6组用按比例分配的分层抽样的方法随机抽取6户做问卷调查,并在这6户中任选2户进行座谈会,求这2户中恰有1户是“月均用水量不低于50吨”的概率.
您最近半年使用:0次
8 . 我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米 石,验得米内夹谷,抽样取米一把,数得
石,验得米内夹谷,抽样取米一把,数得 粒内夹谷
粒内夹谷 粒,则这批米内夹谷约为( )
粒,则这批米内夹谷约为( )
 石,验得米内夹谷,抽样取米一把,数得
石,验得米内夹谷,抽样取米一把,数得 粒内夹谷
粒内夹谷 粒,则这批米内夹谷约为( )
粒,则这批米内夹谷约为( )A. 石 石 | B. 石 石 | C.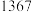 石 石 | D.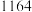 石 石 |
您最近半年使用:0次
解题方法
9 . 甲、乙两台机床生产同种产品,产品按质量分为一级品和二级品,为了比较两台机床产品的质量,分别用两台机床各生产了 件产品,产品的质量情况统计如下表:
件产品,产品的质量情况统计如下表:
(1)甲机床、乙机床生产的产品中一级品的频率分别是多少?
(2)根据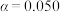 的独立性检验,能否认为甲机床的产品质量与乙机床的产品质量有差异?
的独立性检验,能否认为甲机床的产品质量与乙机床的产品质量有差异?
附:
 件产品,产品的质量情况统计如下表:
件产品,产品的质量情况统计如下表:一级品 | 二级品 | 合计 | |
甲机床 |
|
|
|
乙机床 |
|
|
|
合计 |
|
|
|
(2)根据
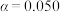 的独立性检验,能否认为甲机床的产品质量与乙机床的产品质量有差异?
的独立性检验,能否认为甲机床的产品质量与乙机床的产品质量有差异?附:

|
|
|
|
|
|
|
|
您最近半年使用:0次
10 . 为了研究高三年级学生的性别和身高是否大于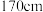 的关联性,同学甲调查丁某中学高三年级所有学生,整理得到列联表1,同学乙从该校高三学生中获取容量为40的有放回简单随机样本,由样本数据整理得到列联表2.
的关联性,同学甲调查丁某中学高三年级所有学生,整理得到列联表1,同学乙从该校高三学生中获取容量为40的有放回简单随机样本,由样本数据整理得到列联表2.
表1单位:人
表2单位:人
(1)利用表1,通过比较不低于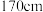 的学生在女生和男生中的比率,判断该中学高三年级学生的性别和身高是否有关联,如果有关联,请解释它们之间如何相互影响;
的学生在女生和男生中的比率,判断该中学高三年级学生的性别和身高是否有关联,如果有关联,请解释它们之间如何相互影响;
(2)利用表2,依据 的独立性检验,推断该中学高三年级学生的性别和身高是否有关联,并解释所得结论的实际含义:
的独立性检验,推断该中学高三年级学生的性别和身高是否有关联,并解释所得结论的实际含义:
(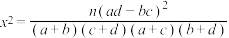 ,
, )
)
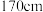 的关联性,同学甲调查丁某中学高三年级所有学生,整理得到列联表1,同学乙从该校高三学生中获取容量为40的有放回简单随机样本,由样本数据整理得到列联表2.
的关联性,同学甲调查丁某中学高三年级所有学生,整理得到列联表1,同学乙从该校高三学生中获取容量为40的有放回简单随机样本,由样本数据整理得到列联表2.表1单位:人
| 性别 | 身高 | 合计 | |
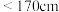 | 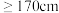 | ||
| 女 | 81 | 16 | 97 |
| 男 | 28 | 75 | 103 |
| 合计 | 109 | 91 | 200 |
| 性别 | 身高 | 合计 | |
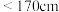 | 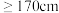 | ||
| 女 | 15 | 6 | 21 |
| 男 | 9 | 10 | 19 |
| 合计 | 24 | 16 | 40 |
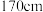 的学生在女生和男生中的比率,判断该中学高三年级学生的性别和身高是否有关联,如果有关联,请解释它们之间如何相互影响;
的学生在女生和男生中的比率,判断该中学高三年级学生的性别和身高是否有关联,如果有关联,请解释它们之间如何相互影响;(2)利用表2,依据
 的独立性检验,推断该中学高三年级学生的性别和身高是否有关联,并解释所得结论的实际含义:
的独立性检验,推断该中学高三年级学生的性别和身高是否有关联,并解释所得结论的实际含义:(
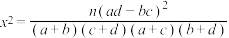 ,
, )
)
您最近半年使用:0次