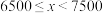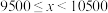1 . 据中国日报网报道:TOP500发布的最新一期全球超级计算机500强榜单显示,中国超算在前五名中占据两席.其中超算全球第一“神威·太湖之光”完全使用了国产处理器.为了了解国产品牌处理器打开文件的速度,某调查公司对两种国产品牌处理器进行了12次测试,结果如下:(数值越小 ,速度越快 ,单位是MIPS)
经过了解,前6次测试是打开含有文字与表格的文件,后6次测试是打开含有文字与图片的文件.请你依据表中数据,运用所学的统计知识,对这两种国产品牌处理器打开文件的速度进行评价.
| 测试1 | 测试2 | 测试3 | 测试4 | 测试5 | 测试6 | 测试7 | 测试8 | 测试9 | 测试10 | 测试11 | 测试12 | |
| 品牌A | 3 | 6 | 9 | 10 | 4 | 1 | 12 | 17 | 4 | 6 | 6 | 14 |
| 品牌B | 2 | 8 | 5 | 4 | 2 | 5 | 8 | 15 | 5 | 12 | 10 | 21 |
您最近一年使用:0次
名校
解题方法
2 . 某市电视台举办纪念红军长征胜利知识回答活动,宣传长征精神,首先在甲、乙、丙、丁四个不同的公园进行支持签名活动.
然后在各公园签名的人中按分层抽样的方式抽取10名幸运之星回答问题,从10个关于长征的问题中随机抽取4个问题让幸运之星回答,全部答对的幸运之星获得一份纪念品.
(1)求此活动中各公园幸运之星的人数;
(2)若乙公园中每位幸运之星对每个问题答对的概率均为 ,求乙公园中恰好2位幸运之星获得纪念品的概率;
,求乙公园中恰好2位幸运之星获得纪念品的概率;
(3)若幸运之星小李对其中8个问题能答对,而另外2个问题答不对,记小李答对的问题数为 ,求
,求 的分布列、期望及方差.
的分布列、期望及方差.
公园 | 甲 | 乙 | 丙 | 丁 |
获得签名人数 | 45 | 60 | 30 | 15 |
(1)求此活动中各公园幸运之星的人数;
(2)若乙公园中每位幸运之星对每个问题答对的概率均为
 ,求乙公园中恰好2位幸运之星获得纪念品的概率;
,求乙公园中恰好2位幸运之星获得纪念品的概率;(3)若幸运之星小李对其中8个问题能答对,而另外2个问题答不对,记小李答对的问题数为
 ,求
,求 的分布列、期望及方差.
的分布列、期望及方差.
您最近一年使用:0次
2020-08-03更新
|
308次组卷
|
2卷引用:甘肃省武威市民勤县第一中学2019-2020学年高二第二学期期末考试数学(理科)试题
名校
3 . “十一”黄金周某公园迎来了旅游高峰期,为了引导游客有序游园,该公园每天分别在 时,
时, 时,
时, 时,
时,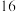 时公布实时在园人数.下表记录了
时公布实时在园人数.下表记录了 月
月 日至
日至 日的实时在园人数:
日的实时在园人数:
通常用公园实时在园人数与公园的最大承载量(同一时段在园人数的饱和量)之比来表示游园舒适度, 以下称为“舒适”,已知该公园的最大承载量是
以下称为“舒适”,已知该公园的最大承载量是 万人.
万人.
(Ⅰ)甲同学从 月
月 日至
日至 日中随机选
日中随机选 天的下午
天的下午 时去该公园游览,求他遇上“舒适”的概率;
时去该公园游览,求他遇上“舒适”的概率;
(Ⅱ)从 月
月 日至
日至 日中任选两天,记这两天中这
日中任选两天,记这两天中这 个时间的游览舒适度都为“舒适”的天数为
个时间的游览舒适度都为“舒适”的天数为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)根据 月
月 日至
日至 日每天
日每天 时的在园人数,判断从哪天开始连续三天
时的在园人数,判断从哪天开始连续三天 时的在园人数的方差最大?(只需写出结论)
时的在园人数的方差最大?(只需写出结论)
 时,
时, 时,
时, 时,
时,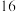 时公布实时在园人数.下表记录了
时公布实时在园人数.下表记录了 月
月 日至
日至 日的实时在园人数:
日的实时在园人数: 日 日 |  日 日 |  日 日 |  日 日 |  日 日 |  日 日 |  日 日 | |
 时在园人数 时在园人数 | 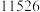 | 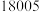 |  |  | 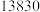 | 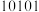 |  |
 时在园人数 时在园人数 | 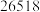 | 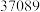 |  |  |  |  |  |
 时在园人数 时在园人数 |  | 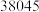 | 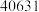 | 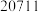 | 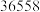 | 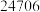 |  |
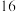 时在园人数 时在园人数 |  |  |  | 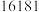 | 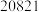 |  | 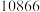 |
 以下称为“舒适”,已知该公园的最大承载量是
以下称为“舒适”,已知该公园的最大承载量是 万人.
万人.(Ⅰ)甲同学从
 月
月 日至
日至 日中随机选
日中随机选 天的下午
天的下午 时去该公园游览,求他遇上“舒适”的概率;
时去该公园游览,求他遇上“舒适”的概率;(Ⅱ)从
 月
月 日至
日至 日中任选两天,记这两天中这
日中任选两天,记这两天中这 个时间的游览舒适度都为“舒适”的天数为
个时间的游览舒适度都为“舒适”的天数为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;(Ⅲ)根据
 月
月 日至
日至 日每天
日每天 时的在园人数,判断从哪天开始连续三天
时的在园人数,判断从哪天开始连续三天 时的在园人数的方差最大?(只需写出结论)
时的在园人数的方差最大?(只需写出结论)
您最近一年使用:0次
2020-06-15更新
|
433次组卷
|
3卷引用:北京市房山区2020届高三第二次模拟检测数学试题
名校
4 . 在考察疫情防控工作中,某区卫生防控中心提出了“要坚持开展爱国卫生运动,从人居环境改善、饮食习惯、社会心理健康、公共卫生设施等多个方面开展,特别是要坚决杜绝食用野生动物的陋习,提倡文明健康、绿色环保的生活方式”的要求.某小组通过问卷调查,随机收集了该区居民六类日常生活习惯的有关数据.六类习惯是:(1)卫生习惯状况类;(2)垃圾处理状况类;(3)体育锻炼状况类;(4)心理健康状况类;(5)膳食合理状况类;(6)作息规律状况类.经过数据整理,得到下表:
假设每份调查问卷只调查上述六类状况之一,各类调查是否达到良好标准相互独立.
(1)从小组收集的有效答卷中随机选取1份,求这份试卷的调查结果是膳食合理状况类中习惯良好者的概率;
(2)从该区任选一位居民,试估计他在“卫生习惯状况类、体育锻炼状况类、膳食合理状况类”三类习惯方面,至少具备两类良好习惯的概率;
(3)利用上述六类习惯调查的排序,用“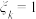 ”表示任选一位第k类受访者是习惯良好者,“
”表示任选一位第k类受访者是习惯良好者,“ ”表示任选一位第k类受访者不是习惯良好者(
”表示任选一位第k类受访者不是习惯良好者(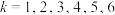 ).写出方差
).写出方差 ,
,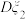 ,
,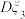 ,
, ,
, ,
,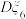 的大小关系.
的大小关系.
| 卫生习惯状况类 | 垃圾处理状况类 | 体育锻炼状况类 | 心理健康状况类 | 膳食合理状况类 | 作息规律状况类 | |
| 有效答卷份数 | 380 | 550 | 330 | 410 | 400 | 430 |
| 习惯良好频率 | 0.6 | 0.9 | 0.8 | 0.7 | 0.65 | 0.6 |
(1)从小组收集的有效答卷中随机选取1份,求这份试卷的调查结果是膳食合理状况类中习惯良好者的概率;
(2)从该区任选一位居民,试估计他在“卫生习惯状况类、体育锻炼状况类、膳食合理状况类”三类习惯方面,至少具备两类良好习惯的概率;
(3)利用上述六类习惯调查的排序,用“
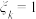 ”表示任选一位第k类受访者是习惯良好者,“
”表示任选一位第k类受访者是习惯良好者,“ ”表示任选一位第k类受访者不是习惯良好者(
”表示任选一位第k类受访者不是习惯良好者(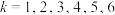 ).写出方差
).写出方差 ,
,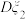 ,
,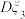 ,
, ,
, ,
,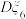 的大小关系.
的大小关系.
您最近一年使用:0次
2020-04-28更新
|
376次组卷
|
3卷引用:2020届北京市密云区高三下学期第一次阶段性测试(一模)数学试题
名校
解题方法
5 . 设盒子中装有6个红球,4个白球,2个黑球,且规定:取出一个红球得 分,取出一个白球得
分,取出一个白球得 分,取出一个黑球得
分,取出一个黑球得 分,其中
分,其中 ,
, ,
, 都为正整数.
都为正整数.
(1)当 ,
, ,
, 时,从该盒子中依次任取(有放回,且每球取到的机会均等)2个球,记随机变量
时,从该盒子中依次任取(有放回,且每球取到的机会均等)2个球,记随机变量 为取出此2球所得分数之和,求
为取出此2球所得分数之和,求 的分布列;
的分布列;
(2)当 时,从该盒子中任取(每球取到的机会均等)1个球,记随机变量
时,从该盒子中任取(每球取到的机会均等)1个球,记随机变量 为取出此球所得分数,若
为取出此球所得分数,若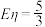 ,
, ,求
,求 和
和 .
.
 分,取出一个白球得
分,取出一个白球得 分,取出一个黑球得
分,取出一个黑球得 分,其中
分,其中 ,
, ,
, 都为正整数.
都为正整数.(1)当
 ,
, ,
, 时,从该盒子中依次任取(有放回,且每球取到的机会均等)2个球,记随机变量
时,从该盒子中依次任取(有放回,且每球取到的机会均等)2个球,记随机变量 为取出此2球所得分数之和,求
为取出此2球所得分数之和,求 的分布列;
的分布列;(2)当
 时,从该盒子中任取(每球取到的机会均等)1个球,记随机变量
时,从该盒子中任取(每球取到的机会均等)1个球,记随机变量 为取出此球所得分数,若
为取出此球所得分数,若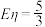 ,
, ,求
,求 和
和 .
.
您最近一年使用:0次
名校
6 . 为了解某地区初中学生的体质健康情况,统计了该地区8所学校学生的体质健康数据,按总分评定等级为优秀,良好,及格,不及格.良好及其以上的比例之和超过40%的学校为先进校.各等级学生人数占该校学生总人数的比例如下表:
(1)从8所学校中随机选出一所学校,求该校为先进校的概率;
(2)从8所学校中随机选出两所学校,记这两所学校中不及格比例低于30%的学校个数为X,求X的分布列;
(3)设8所学校优秀比例的方差为 ,良好及其以下比例之和的方差为
,良好及其以下比例之和的方差为 ,比较
,比较 与
与 的大小.(只写出结果)
的大小.(只写出结果)
| 比例 学校 等级 | 学校A | 学校B | 学校C | 学校D | 学校E | 学校F | 学校G | 学校H |
| 优秀 | 8% | 3% | 2% | 9% | 1% | 22% | 2% | 3% |
| 良好 | 37% | 50% | 23% | 30% | 45% | 46% | 37% | 35% |
| 及格 | 22% | 30% | 33% | 26% | 22% | 17% | 23% | 38% |
| 不及格 | 33% | 17% | 42% | 35% | 32% | 15% | 38% | 24% |
(1)从8所学校中随机选出一所学校,求该校为先进校的概率;
(2)从8所学校中随机选出两所学校,记这两所学校中不及格比例低于30%的学校个数为X,求X的分布列;
(3)设8所学校优秀比例的方差为
 ,良好及其以下比例之和的方差为
,良好及其以下比例之和的方差为 ,比较
,比较 与
与 的大小.(只写出结果)
的大小.(只写出结果)
您最近一年使用:0次
2020-02-09更新
|
519次组卷
|
8卷引用:2020届北京市通州区高三第一学期期末考试数学试题
2020届北京市通州区高三第一学期期末考试数学试题(已下线)专题01 少丢分题目强化卷(第二篇)-备战2021年新高考数学分层强化训练(北京专版)(已下线)专题03 少丢分题目强化卷(第二篇)-备战2021年新高考数学分层强化训练(北京专版)(已下线)专题10 必拿分题目强化卷(第一篇)-备战2021年新高考数学分层强化训练(北京专版)2020届山东省济宁市嘉祥一中高三下学期第一次质量检测数学试题人教B版(2019) 选择性必修第二册 过关斩将 第四章 概率与统计 4.2 随机变量 专题强化练5 离散型随机变量的分布列及数字特征北京市北京师范大学第二附属中学2023-2024学年高二下学期第二次月考数学试题陕西省咸阳市武功县普集高中2021-2022学年高一重点班下学期第一次月考数学试题
解题方法
7 . 某校在学年期末举行“我最喜欢的文化课”评选活动,投票规则是一人一票,高一(1)班44名学生和高一(7)班45名学生的投票结果如下表(无废票):
该校把上表的数据作为样本,把两个班同一学科的得票之和定义为该年级该学科的“好感指数”.
(Ⅰ)如果数学学科的“好感指数”比高一年级其他文化课都高,求 的所有取值;
的所有取值;
(Ⅱ)从高一(1)班投票给政治、历史、地理的学生中任意选取 位同学,设随机变量
位同学,设随机变量 为投票给地理学科的人数,求
为投票给地理学科的人数,求 的分布列和期望;
的分布列和期望;
(Ⅲ)当 为何值时,高一年级的语文、数学、外语三科的“好感指数”的方差最小?(结论不要求证明)
为何值时,高一年级的语文、数学、外语三科的“好感指数”的方差最小?(结论不要求证明)
| 语文 | 数学 | 外语 | 物理 | 化学 | 生物 | 政治 | 历史 | 地理 | |
| 高一(1)班 | 6 | 9 | 7 | 5 | 4 | 5 | 3 | 3 | 2 |
| 高一(7)班 |  | 6 |  | 4 | 5 | 6 | 5 | 2 | 3 |
(Ⅰ)如果数学学科的“好感指数”比高一年级其他文化课都高,求
 的所有取值;
的所有取值;(Ⅱ)从高一(1)班投票给政治、历史、地理的学生中任意选取
 位同学,设随机变量
位同学,设随机变量 为投票给地理学科的人数,求
为投票给地理学科的人数,求 的分布列和期望;
的分布列和期望;(Ⅲ)当
 为何值时,高一年级的语文、数学、外语三科的“好感指数”的方差最小?(结论不要求证明)
为何值时,高一年级的语文、数学、外语三科的“好感指数”的方差最小?(结论不要求证明)
您最近一年使用:0次
8 . 某工厂的机器上存在一种易损元件,这种元件发生损坏时,需要及时维修. 现有甲、乙两名工人同时从事这项工作,下表记录了某月1日到10日甲、乙两名工人分别维修这种元件的件数.
(1)从这 天中,随机选取一天,求甲维修的元件数不少于5件的概率;
天中,随机选取一天,求甲维修的元件数不少于5件的概率;
(2)试比较这10天中甲维修的元件数的方差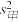 与乙维修的元件数的方差
与乙维修的元件数的方差 的大小.(只需写出结论);
的大小.(只需写出结论);
(3)由于甲、乙的任务量大,拟增加工人,为使增加工人后平均每人每天维修的元件不超过3件,请利用上表数据估计最少需要增加几名工人.
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 | 8日 | 9日 | 10日 |
| 甲维修的元件数 | 3 | 5 | 4 | 6 | 4 | 6 | 3 | 7 | 8 | 4 |
| 乙维修的元件数 | 4 | 7 | 4 | 5 | 5 | 4 | 5 | 5 | 4 | 7 |
(1)从这
 天中,随机选取一天,求甲维修的元件数不少于5件的概率;
天中,随机选取一天,求甲维修的元件数不少于5件的概率;(2)试比较这10天中甲维修的元件数的方差
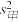 与乙维修的元件数的方差
与乙维修的元件数的方差 的大小.(只需写出结论);
的大小.(只需写出结论);(3)由于甲、乙的任务量大,拟增加工人,为使增加工人后平均每人每天维修的元件不超过3件,请利用上表数据估计最少需要增加几名工人.
您最近一年使用:0次
名校
9 . 2020年我国全面建成小康社会,其中小康生活的住房标准是城镇人均住房建筑面积30平方米. 下表为2007年—2016年中,我区城镇和农村人均住房建筑面积统计数据. 单位:平方米.
(Ⅰ)现从上述表格中随机抽取连续两年数据,求这两年中城镇人均住房建筑面积增长不少于2平方米的概率;
(Ⅱ)在给出的10年数据中,随机抽取三年,记 为同年中农村人均住房建筑面积超过城镇人均住房建筑面积4平方米的年数,求
为同年中农村人均住房建筑面积超过城镇人均住房建筑面积4平方米的年数,求 的分布列和数学期望
的分布列和数学期望 ;
;
(Ⅲ)将城镇和农村的人均住房建筑面积经四舍五入取整后作为样本数据.记2012—2016年中城镇人均住房面积的方差为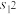 ,农村人均住房面积的方差为
,农村人均住房面积的方差为 ,判断
,判断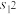 与
与 的大小.(只需写出结论).
的大小.(只需写出结论).
2007年 | 2008年 | 2009年 | 2010年 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | |
城镇 | 18.66 | 20.25 | 22.79 | 25 | 27.1 | 28.3 | 31.6 | 32.9 | 34.6 | 36.6 |
农村 | 23.3 | 24.8 | 26.5 | 27.9 | 30.7 | 32.4 | 34.1 | 37.1 | 41.2 | 45.8 |
(Ⅰ)现从上述表格中随机抽取连续两年数据,求这两年中城镇人均住房建筑面积增长不少于2平方米的概率;
(Ⅱ)在给出的10年数据中,随机抽取三年,记
 为同年中农村人均住房建筑面积超过城镇人均住房建筑面积4平方米的年数,求
为同年中农村人均住房建筑面积超过城镇人均住房建筑面积4平方米的年数,求 的分布列和数学期望
的分布列和数学期望 ;
;(Ⅲ)将城镇和农村的人均住房建筑面积经四舍五入取整后作为样本数据.记2012—2016年中城镇人均住房面积的方差为
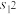 ,农村人均住房面积的方差为
,农村人均住房面积的方差为 ,判断
,判断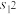 与
与 的大小.(只需写出结论).
的大小.(只需写出结论).
您最近一年使用:0次
2019-04-03更新
|
790次组卷
|
4卷引用:【区级联考】北京延庆区2019届高三一模数学(理)试题
【区级联考】北京延庆区2019届高三一模数学(理)试题北京五中2020届高三(4月份)高考数学模拟试题(已下线)专题18 统计综合-2020年高考数学母题题源解密(北京专版)北京市第五中学2021-2022学年高二下学期期中数学试题
名校
10 . 由于研究性学习的需要,中学生李华持续收集了手机“微信运动”团队中特定20名成员每天行走的步数,其中某一天的数据记录如下:
5860 6520 7326 6798 7325 8430 8215 7453 7446 6754
7638 6834 6460 6830 9860 8753 9450 9860 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表(设步数为 )
)
(Ⅰ)写出 的值,并回答这20名“微信运动”团队成员一天行走步数的中位数落在哪个组别;
的值,并回答这20名“微信运动”团队成员一天行走步数的中位数落在哪个组别;
(Ⅱ)记 组步数数据的平均数与方差分别为
组步数数据的平均数与方差分别为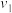 ,
, ,
, 组步数数据的平均数与方差分别为
组步数数据的平均数与方差分别为 ,
, ,试分别比较
,试分别比较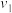 与以
与以 ,
, 与
与 的大小;(只需写出结论)
的大小;(只需写出结论)
(Ⅲ)从上述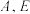 两个组别的数据中任取2个数据,记这2个数据步数差的绝对值为
两个组别的数据中任取2个数据,记这2个数据步数差的绝对值为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
5860 6520 7326 6798 7325 8430 8215 7453 7446 6754
7638 6834 6460 6830 9860 8753 9450 9860 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表(设步数为
 )
)组别 | 步数分组 | 频数 |
|
| 2 |
|
| 10 |
|
|
|
|
| 2 |
|
|
|
 的值,并回答这20名“微信运动”团队成员一天行走步数的中位数落在哪个组别;
的值,并回答这20名“微信运动”团队成员一天行走步数的中位数落在哪个组别;(Ⅱ)记
 组步数数据的平均数与方差分别为
组步数数据的平均数与方差分别为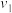 ,
, ,
, 组步数数据的平均数与方差分别为
组步数数据的平均数与方差分别为 ,
, ,试分别比较
,试分别比较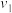 与以
与以 ,
, 与
与 的大小;(只需写出结论)
的大小;(只需写出结论)(Ⅲ)从上述
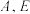 两个组别的数据中任取2个数据,记这2个数据步数差的绝对值为
两个组别的数据中任取2个数据,记这2个数据步数差的绝对值为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
您最近一年使用:0次
2018-06-16更新
|
427次组卷
|
2卷引用:【全国百强校】北京市十一学校2018届高三三模数学(文理)试题