2020高三·全国·专题练习
解题方法
1 . 我市某大学组建了 、
、 、
、 、
、 、
、 五个不同的社团组织,为培养学生的兴趣爱好,要求每个学生必须且只能参加一个社团,假定某寝室的甲、乙、丙三名学生对这五个社团的选择是等可能的.
五个不同的社团组织,为培养学生的兴趣爱好,要求每个学生必须且只能参加一个社团,假定某寝室的甲、乙、丙三名学生对这五个社团的选择是等可能的.
(1)求甲、乙、丙三名学生中至少有两人参加同一社团的概率;
(2)设随机变量 为甲、乙、丙这三个学生参加
为甲、乙、丙这三个学生参加 或
或 社团的人数,求
社团的人数,求 的分布列、数学期望及方差.
的分布列、数学期望及方差.
 、
、 、
、 、
、 、
、 五个不同的社团组织,为培养学生的兴趣爱好,要求每个学生必须且只能参加一个社团,假定某寝室的甲、乙、丙三名学生对这五个社团的选择是等可能的.
五个不同的社团组织,为培养学生的兴趣爱好,要求每个学生必须且只能参加一个社团,假定某寝室的甲、乙、丙三名学生对这五个社团的选择是等可能的.(1)求甲、乙、丙三名学生中至少有两人参加同一社团的概率;
(2)设随机变量
 为甲、乙、丙这三个学生参加
为甲、乙、丙这三个学生参加 或
或 社团的人数,求
社团的人数,求 的分布列、数学期望及方差.
的分布列、数学期望及方差.
您最近一年使用:0次
2 . 红铃虫是棉花的主要害虫之一,能对农作物造成严重伤害.每只红铃虫的平均产卵数 和平均温度
和平均温度 有关.现收集了以往某地的7组数据,得到下面的散点图及一些统计量的值.
有关.现收集了以往某地的7组数据,得到下面的散点图及一些统计量的值.
表中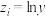 ,
,
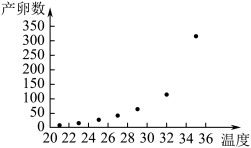
(1)根据散点图判断, 与
与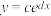 (其中
(其中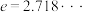 为自然对数的底数)哪一个更适宜作为平均产卵数
为自然对数的底数)哪一个更适宜作为平均产卵数 关于平均温度
关于平均温度 的回归方程类型?(给出判断即可不必说明理由)并由判断结果及表中数据,求出
的回归方程类型?(给出判断即可不必说明理由)并由判断结果及表中数据,求出 关于
关于 的回归方程.(计算结果精确到小数点后第三位)
的回归方程.(计算结果精确到小数点后第三位)
(2)根据以往统计,该地每年平均温度达到28℃以上时红铃虫会造成严重伤害,需要人工防治,其他情况均不需要人工防治,记该地每年平均温度达到28℃以上的概率为 .
.
(ⅰ)记该地今后5年中,恰好需要3次人工防治的概率为 ,求
,求 的最大值,并求出相应的概率
的最大值,并求出相应的概率 .
.
(ⅱ)当 取最大值时,记该地今后5年中,需要人工防治的次数为
取最大值时,记该地今后5年中,需要人工防治的次数为 ,求
,求 的数学期望和方差.
的数学期望和方差.
附:对于一组数据 ,其回归直线
,其回归直线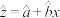 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为: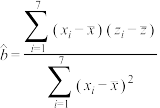 ,
,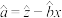 .
.
 和平均温度
和平均温度 有关.现收集了以往某地的7组数据,得到下面的散点图及一些统计量的值.
有关.现收集了以往某地的7组数据,得到下面的散点图及一些统计量的值.平均温度 /℃ /℃ | 21 | 23 | 25 | 27 | 29 | 32 | 35 | |||||
平均产卵数 /个 /个 | 7 | 11 | 21 | 24 | 66 | 115 | 325 | |||||
 | 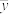 |  | 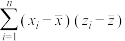 | 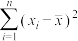 | ||||||||
| 27.429 | 81.286 | 3.612 | 40.182 | 147.714 | ||||||||
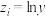 ,
,

(1)根据散点图判断,
 与
与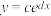 (其中
(其中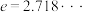 为自然对数的底数)哪一个更适宜作为平均产卵数
为自然对数的底数)哪一个更适宜作为平均产卵数 关于平均温度
关于平均温度 的回归方程类型?(给出判断即可不必说明理由)并由判断结果及表中数据,求出
的回归方程类型?(给出判断即可不必说明理由)并由判断结果及表中数据,求出 关于
关于 的回归方程.(计算结果精确到小数点后第三位)
的回归方程.(计算结果精确到小数点后第三位)(2)根据以往统计,该地每年平均温度达到28℃以上时红铃虫会造成严重伤害,需要人工防治,其他情况均不需要人工防治,记该地每年平均温度达到28℃以上的概率为
 .
.(ⅰ)记该地今后5年中,恰好需要3次人工防治的概率为
 ,求
,求 的最大值,并求出相应的概率
的最大值,并求出相应的概率 .
.(ⅱ)当
 取最大值时,记该地今后5年中,需要人工防治的次数为
取最大值时,记该地今后5年中,需要人工防治的次数为 ,求
,求 的数学期望和方差.
的数学期望和方差.附:对于一组数据
 ,其回归直线
,其回归直线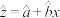 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为: ,
,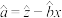 .
.
您最近一年使用:0次
2020-12-06更新
|
1137次组卷
|
15卷引用:2020届海南省海口市海南中学高三第六次月考试卷数学
2020届海南省海口市海南中学高三第六次月考试卷数学2020届山东省日照第一中学高三上学期期中数学试题2019届湖北省黄冈中学、华师一附中、襄阳四中、襄阳五中、荆州中学等八校高三第二次联考数学(理)试题广东省深圳外国语学校2020届高三下学期第6次月考数学(理)试题广东省汕头市金山中学2019-2020学年高二下学期6月月考数学试题(已下线)痛点16 概率与统计中的综合问题-2021年新高考数学一轮复习考点扫描(已下线)第十一单元 概率与统计(B卷 滚动提升检测)-2021年高考数学(理)一轮复习单元滚动双测卷河北正定中学2021届高三上学期第三次半月考数学试题安徽省六校教育研究会2021届高三下学期2月第二次联考理科数学试题(已下线)8.2 一元线性回归模型及其应用(精练)-2020-2021学年高二数学一隅三反系列(人教A版2019选择性必修第三册)(已下线)黄金卷02-【赢在高考·黄金20卷】备战2021年高考数学全真模拟卷(山东高考专用)(已下线)专题23 概率与统计相结合问题(讲)-2021年高三数学二轮复习讲练测(新高考版)(已下线)专题27 概率与统计相结合问题(讲)-2021年高三数学二轮复习讲练测(文理通用)安徽省六安市舒城中学2021届高三下学期高考仿真(一)理科数学试题(已下线)第八章 成对数据的统计分析(选拔卷)-【单元测试】2021-2022学年高二数学尖子生选拔卷(人教A版2019选择性必修第三册)
解题方法
3 . 高考改革后,学生除了语数外三门必选外,可在A类科目:物理、化学、生物和B类科目:政治、地理、历史共6个科目中任选3门.
(1)若小明同学已经确定选了物理,现在他还要从剩余的5科中再选2科,则他在历史与地理两科中至少选一科的概率?
(2)求小明同学选A类科目数X的分布列、数学期望和方差.
(1)若小明同学已经确定选了物理,现在他还要从剩余的5科中再选2科,则他在历史与地理两科中至少选一科的概率?
(2)求小明同学选A类科目数X的分布列、数学期望和方差.
您最近一年使用:0次
名校
4 . 10月1日,某品牌的两款最新手机(记为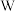 型号,
型号, 型号)同时投放市场,手机厂商为了解这两款手机的销售情况,在10月1日当天,随机调查了5个手机店中这两款手机的销量(单位:部),得到下表:
型号)同时投放市场,手机厂商为了解这两款手机的销售情况,在10月1日当天,随机调查了5个手机店中这两款手机的销量(单位:部),得到下表:
(Ⅰ)若在10月1日当天,从 ,
,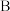 这两个手机店售出的新款手机中各随机抽取1部,求抽取的2部手机中至少有一部为
这两个手机店售出的新款手机中各随机抽取1部,求抽取的2部手机中至少有一部为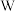 型号手机的概率;
型号手机的概率;
(Ⅱ)现从这5个手机店中任选3个举行促销活动,用 表示其中
表示其中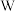 型号手机销量超过
型号手机销量超过 型号手机销量的手机店的个数,求随机变量
型号手机销量的手机店的个数,求随机变量 的分布列和数学期望;
的分布列和数学期望;
(III)经测算,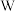 型号手机的销售成本
型号手机的销售成本 (百元)与销量(部)满足关系
(百元)与销量(部)满足关系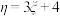 .若表中
.若表中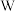 型号手机销量的方差
型号手机销量的方差 ,试给出表中5个手机店的
,试给出表中5个手机店的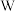 型号手机销售成本的方差
型号手机销售成本的方差 的值.(用
的值.(用 表示,结论不要求证明)
表示,结论不要求证明)
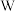 型号,
型号, 型号)同时投放市场,手机厂商为了解这两款手机的销售情况,在10月1日当天,随机调查了5个手机店中这两款手机的销量(单位:部),得到下表:
型号)同时投放市场,手机厂商为了解这两款手机的销售情况,在10月1日当天,随机调查了5个手机店中这两款手机的销量(单位:部),得到下表:| 手机店 |  | 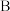 | 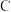 | 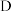 |  |
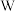 型号手机销量 型号手机销量 | 6 | 6 | 13 | 8 | 11 |
 型号手机销量 型号手机销量 | 12 | 9 | 13 | 6 | 4 |
 ,
,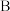 这两个手机店售出的新款手机中各随机抽取1部,求抽取的2部手机中至少有一部为
这两个手机店售出的新款手机中各随机抽取1部,求抽取的2部手机中至少有一部为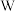 型号手机的概率;
型号手机的概率;(Ⅱ)现从这5个手机店中任选3个举行促销活动,用
 表示其中
表示其中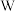 型号手机销量超过
型号手机销量超过 型号手机销量的手机店的个数,求随机变量
型号手机销量的手机店的个数,求随机变量 的分布列和数学期望;
的分布列和数学期望;(III)经测算,
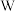 型号手机的销售成本
型号手机的销售成本 (百元)与销量(部)满足关系
(百元)与销量(部)满足关系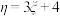 .若表中
.若表中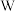 型号手机销量的方差
型号手机销量的方差 ,试给出表中5个手机店的
,试给出表中5个手机店的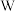 型号手机销售成本的方差
型号手机销售成本的方差 的值.(用
的值.(用 表示,结论不要求证明)
表示,结论不要求证明)
您最近一年使用:0次
2019-06-12更新
|
1926次组卷
|
7卷引用:海南省华侨中学2019-2020学年高二(6月)第二次阶段性考试数学试题
海南省华侨中学2019-2020学年高二(6月)第二次阶段性考试数学试题【全国百强校】湖北省黄冈中学2019届高三第三次模拟考试数学(理)试题2020届山东省青岛二中高三上学期10月月考数学试题河北省邯郸一中2019-2020学年高三下学期第九次模拟数学试题(已下线)专题06 离散型随机变量的期望与方差(第四篇)-备战2020年高考数学大题精做之解答题题型全覆盖安徽省淮北市第一中学2020届高三下学期第七次月考数学(理)试题人教A版(2019) 选修第三册 一蹴而就 第七章 7.3 离散型随机变量的数字特征
5 . A、B两个投资项目的利润率分别为随机变量X1和X2.根据市场分析,X1,X2的分布列分别为
(Ⅰ)在A、B两个项目上各投资100万元,Y1和Y2分别表示投资项目A和B所获得的利润,求方差DY1,DY2;
(Ⅱ)将x(0≤x≤100)万元投资A项目,100-x万元投资B项目,f(x)表示投资A项目所得利润的方差与投资B项目所得到利润的方差的和.求f(x)的最小值,并指出x为何值时,f(x)取到最小值.
(注:D(ax+b)=a2Dx)
| X1 | 5% | 10% |
| P | 0.8 | 0.2 |
| X2 | 2% | 8% | 12% |
| P | 0.2 | 0.5 | 0.3 |
(Ⅰ)在A、B两个项目上各投资100万元,Y1和Y2分别表示投资项目A和B所获得的利润,求方差DY1,DY2;
(Ⅱ)将x(0≤x≤100)万元投资A项目,100-x万元投资B项目,f(x)表示投资A项目所得利润的方差与投资B项目所得到利润的方差的和.求f(x)的最小值,并指出x为何值时,f(x)取到最小值.
(注:D(ax+b)=a2Dx)
您最近一年使用:0次
2019-01-30更新
|
2069次组卷
|
17卷引用:2008年普通高等学校招生考试数学(理)试题(琼、宁卷)
2008年普通高等学校招生考试数学(理)试题(琼、宁卷)2008年普通高等学校招生全国统一考试理科数学(宁夏卷)(已下线)2013-2014学年苏教版选修2-3高二数学双基达标2.5练习卷黑龙江省海林市朝鲜族中学人教版高中数学选修2-3同步练习:滚动习题(四)[范围2.1~2.4](已下线)高中数学新教材练习题人教B版(2019) 选修第二册 突围者 第四章 第二节课时4 随机变量的数字特征(已下线)第五课时 课后 7.3.2 离散型随机变量的方差(已下线)第四章 概率与统计 本章小结广东省中山纪念中学等四校2021届高三下学期5月联考数学试卷(已下线)3.2.4 离散型随机变量的方差(已下线)13.3 二项分布、超几何分布与数字特征(已下线)7.3.2 离散型随机变量的方差(2)北师大版(2019) 选修第一册 数学奇书 学业评价(四十二) 离散型随机变量的方差人教B版(2019)选择性必修第二册课本习题第四章本章小结宁夏回族自治区吴忠市吴忠中学2023-2024学年高二下学期6月月考数学试卷【巩固卷】第7章 概率初步(续)单元测试B沪教版(2020)选择性必修第二册【课后练 】3.2.4 离散型随机变量的方差 课后作业-湘教版(2019)选择性必修第二册 第3章 概率
名校
6 . 某地区拟建立一个艺术博物馆,采取竞标的方式从多家建筑公司选取一家建筑公司,经过层层筛选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从 个招标问题中随机抽取
个招标问题中随机抽取 个问题,已知这
个问题,已知这 个招标问题中,甲公司可正确回答其中的
个招标问题中,甲公司可正确回答其中的 道题目,而乙公司能正确回答每道题目的概率均为
道题目,而乙公司能正确回答每道题目的概率均为 ,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
(1)求甲、乙两家公司共答对 道题目的概率;
道题目的概率;
(2)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
 个招标问题中随机抽取
个招标问题中随机抽取 个问题,已知这
个问题,已知这 个招标问题中,甲公司可正确回答其中的
个招标问题中,甲公司可正确回答其中的 道题目,而乙公司能正确回答每道题目的概率均为
道题目,而乙公司能正确回答每道题目的概率均为 ,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
,甲、乙两家公司对每题的回答都是相互独立,互不影响的.(1)求甲、乙两家公司共答对
 道题目的概率;
道题目的概率;(2)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
您最近一年使用:0次
2017-04-13更新
|
814次组卷
|
8卷引用:2017届海南省海口市高三4月调研测试数学(理)试卷
名校
7 . 为回馈顾客,某商场拟通过摸球兑奖的方式对 位顾客进行奖励,规定:每位顾客从一个装有
位顾客进行奖励,规定:每位顾客从一个装有 个标有面值的球的袋中一次性随机摸出
个标有面值的球的袋中一次性随机摸出 个球,球上所标的面值之和为该顾客所获的奖励额.
个球,球上所标的面值之和为该顾客所获的奖励额.
(1)若袋中所装的 个球中有
个球中有 个所标的面值为
个所标的面值为 元,其余
元,其余 个均为
个均为 元,求顾客所获的奖励额的分布列及数学期望;
元,求顾客所获的奖励额的分布列及数学期望;
(2)商场对奖励总额的预算是 元,并规定袋中的
元,并规定袋中的 个球只能由标有面值为
个球只能由标有面值为 元和
元和 元的两种球组成,或标有面值
元的两种球组成,或标有面值 元和
元和 元的两种球组成.为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡.请对袋中的
元的两种球组成.为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡.请对袋中的 个球的面值给出一个合适的设计,并说明理由.
个球的面值给出一个合适的设计,并说明理由.
 位顾客进行奖励,规定:每位顾客从一个装有
位顾客进行奖励,规定:每位顾客从一个装有 个标有面值的球的袋中一次性随机摸出
个标有面值的球的袋中一次性随机摸出 个球,球上所标的面值之和为该顾客所获的奖励额.
个球,球上所标的面值之和为该顾客所获的奖励额. (1)若袋中所装的
 个球中有
个球中有 个所标的面值为
个所标的面值为 元,其余
元,其余 个均为
个均为 元,求顾客所获的奖励额的分布列及数学期望;
元,求顾客所获的奖励额的分布列及数学期望;(2)商场对奖励总额的预算是
 元,并规定袋中的
元,并规定袋中的 个球只能由标有面值为
个球只能由标有面值为 元和
元和 元的两种球组成,或标有面值
元的两种球组成,或标有面值 元和
元和 元的两种球组成.为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡.请对袋中的
元的两种球组成.为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡.请对袋中的 个球的面值给出一个合适的设计,并说明理由.
个球的面值给出一个合适的设计,并说明理由.
您最近一年使用:0次
2016-12-04更新
|
253次组卷
|
2卷引用:2015-2016学年海南文昌中学高二下期末理科数学试卷



