解题方法
1 . 已知随机变量X的分布列为
若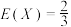 ,
,
(1)求 的值;
的值;
(2)若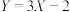 ,求
,求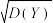 的值.
的值.
X | 0 | 1 | x |
P |
|
| p |
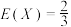 ,
,(1)求
 的值;
的值;(2)若
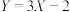 ,求
,求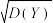 的值.
的值.
您最近一年使用:0次
2023-08-01更新
|
940次组卷
|
21卷引用:高中数学人教A版选修2-3 第二章 随机变量及其分布 2.3.2 离散型随机变量的方差
高中数学人教A版选修2-3 第二章 随机变量及其分布 2.3.2 离散型随机变量的方差西藏自治区拉萨市拉萨那曲第二高级中学2018-2019学年高二下学期期末数学(理)试题辽宁省葫芦岛市实验中学东戴河分校2019-2020学年高二下学期期中考试数学试题(已下线)突破2.3离散型随机变的均值与方差-突破满分数学之2019-2020学年高二数学(理)重难点突破(人教A版选修2-3)(已下线)专题14 计数原理、随机变量的数字特征 第一篇 热点、难点突破篇(讲)-2021年高考数学二轮复习讲练测(浙江专用)(已下线)专题14 计数原理、随机变量的数字特征(讲)--第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测(浙江专用)》北师大版(2019) 选修第一册 突围者 第六章 第三节 课时2 离散型随机变量的方差6.3.2离散型随机变量的方差 同步练习6.3.2离散型随机变量的方差 课时作业新疆博湖县奇石中学2022-2023学年高二下学期期末考试数学试题(已下线)专题21 离散型随机变量的均值、方差与标准差(重点突围)-【学霸满分】2022-2023学年高二数学下学期重难点专题提优训练(苏教版2019选择性必修第二册)(已下线)第07讲 离散型随机变量的分布列与数字特征(六大题型)(讲义)(已下线)第10讲 离散型随机变量的均值与方差-【寒假预科讲义】2024年高二数学寒假精品课(人教A版2019)(已下线)专题12随机变量及其分布 (十六大题型+过关检测专训)(3)(已下线)专题12随机变量及其分布 (十六大题型+过关检测专训)(1)(已下线)第05讲 7.3.2离散型随机变量的方差-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)专题7.8 随机变量及其分布全章十一大压轴题型归纳(拔尖篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)第八章 概率(知识归纳+题型突破)-2023-2024学年高二数学单元速记·巧练(苏教版2019选择性必修第二册)(已下线)7.3.2 离散型随机变量的方差——课后作业(基础版)(已下线)第7.3.2讲 离散型随机变量的方差-2023-2024学年新高二数学同步精讲精练宝典(人教A版2019选修第三册)新疆兵团第三师图木舒克市鸿德实验学校2023-2024学年高二下学期第二次月考数学试卷
2020高三·全国·专题练习
名校
2 . 为迎接2022年北京冬奥会,推广滑雪运动,某滑雪场开展滑雪促销活动.该滑雪场的收费标准是:滑雪时间不超过1小时免费,超过1小时的部分每小时收费标准为40元(不足1小时的部分按1小时计算).有甲、乙两人相互独立地来该滑雪场运动,设甲、乙不超过1小时离开的概率分别为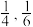 ;1小时以上且不超过2小时离开的概率分别为
;1小时以上且不超过2小时离开的概率分别为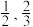 ;两人滑雪时间都不会超过3小时.
;两人滑雪时间都不会超过3小时.
(1)求甲、乙两人所付滑雪费用相同的概率;
(2)设甲、乙两人所付的滑雪费用之和为随机变量ξ,求ξ的分布列与均值E(ξ),方差D(ξ).
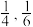 ;1小时以上且不超过2小时离开的概率分别为
;1小时以上且不超过2小时离开的概率分别为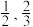 ;两人滑雪时间都不会超过3小时.
;两人滑雪时间都不会超过3小时.(1)求甲、乙两人所付滑雪费用相同的概率;
(2)设甲、乙两人所付的滑雪费用之和为随机变量ξ,求ξ的分布列与均值E(ξ),方差D(ξ).
您最近一年使用:0次
2022-11-08更新
|
2018次组卷
|
32卷引用:专题11.9 离散型随机变量的均值与方差(讲)【理】-《2020年高考一轮复习讲练测》
(已下线)专题11.9 离散型随机变量的均值与方差(讲)【理】-《2020年高考一轮复习讲练测》(已下线)专题06 离散型随机变量的期望与方差(第四篇)-备战2020年高考数学大题精做之解答题题型全覆盖山西省朔州市应县第一中学校2019-2020学年高二下学期期中数学(理)试题(已下线)专题11.5 离散型随机变量的分布列、均值与方差 (精讲)-2021年高考数学(理)一轮复习讲练测浙江省台州市九校联盟2021-2022学年高二下学期期中联考数学试题(已下线)7.3 离散型随机变量的数字特征(精讲)-2020-2021学年高二数学一隅三反系列(人教A版2019选择性必修第三册)(已下线)4.2.4随机变量的数字特征(2)B提高练(已下线)第二章 随机变量及其分布【专项训练】-2020-2021学年高二数学(理)下学期期末专项复习(人教A版选修2-3)(已下线)【新教材精创】7.3.2离散型随机变量的方差 -B提高练辽宁省凤城市第一中学2021-2022学年高三上学期10月月考数学试题人教A版(2019) 选修第三册 实战演练 第七章验收检测宁夏回族自治区银川一中2021-2022学年高二下学期期中考试数学(理)试题广东省佛山市南海一中2021-2022学年高二下学期第二次大测数学试题辽宁省沈阳市市级重点高中联合体2021-2022学年高二下学期期测试末数学试题江苏省苏州外国语学校2021-2022学年高二下学期期末数学试题(已下线)13.3 二项分布、超几何分布与数字特征(已下线)第70讲 随机变量及其概率分布、均值与方差(已下线)7.3.2离散型随机变量的方差(精讲)(已下线)第08讲 离散型随机变量的期望方差及其性质3种题型江苏省淮安市盱眙中学2023届高三七模数学试题(已下线)8.2.2离散型随机变量的数字特征-【帮课堂】2022-2023学年高二数学同步精品讲义(苏教版2019选择性必修第二册)(已下线)7.3.1 离散型随机变量的均值(2)(已下线)7.3.2 离散型随机变量的方差(2)(已下线)7.3.2 离散型随机变量的方差(1)北师大版(2019) 选修第一册 数学奇书 学业评价(四十二) 离散型随机变量的方差江西省上高二中2022-2023学年高二下学期2月月考数学试题(已下线)7.3离散型随机变量的数字特征 第二练 强化考点训练江苏省扬州市广陵区红桥高级中学2023-2024学年高二下学期期中考试数学试题湖北省荆州中学2024届高三下学期第三次适应性考试数学试题【江苏专用】专题08概率与统计(第五部分)-高二下学期名校期末好题汇编(已下线)专题05 离散型随机变量的分布列常考点(8类题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(江苏专用)【基础卷】第7章 概率初步(续)单元测试C-沪教版(2020)选择性必修第二册
名校
解题方法
3 . 甲口袋里有大小相同编号不同的2个黑球和3个白球,乙口袋里有大小相同编号不同的3个黑球和2个白球,现从甲口袋中取出3个球,记黑球个数为 ,从乙口袋中也取出3个球,记黑球个数为
,从乙口袋中也取出3个球,记黑球个数为 .
.
(1)求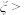
 时的概率;
时的概率;
(2)若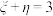 ,求随机变量
,求随机变量 的数学期望
的数学期望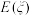 及
及 的方差
的方差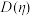 .
.
 ,从乙口袋中也取出3个球,记黑球个数为
,从乙口袋中也取出3个球,记黑球个数为 .
.(1)求
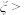
 时的概率;
时的概率;(2)若
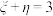 ,求随机变量
,求随机变量 的数学期望
的数学期望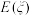 及
及 的方差
的方差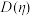 .
.
您最近一年使用:0次
20-21高二上·全国·单元测试
名校
4 . 甲、乙两名射手在一次射击中得分为两个相互独立的随机变量ξ与η,且ξ,η的分布列为:
(1)求a,b的值;
(2)计算ξ,η的期望与方差,并以此分析甲、乙技术状况.
ξ | 1 | 2 | 3 |
P | a | 0.1 | 0.6 |
η | 1 | 2 | 3 |
P | 0.3 | b | 0.3 |
(2)计算ξ,η的期望与方差,并以此分析甲、乙技术状况.
您最近一年使用:0次
2021-01-07更新
|
657次组卷
|
12卷引用:人教B版2019选择性必修第二册综合测试(能力提升)-2020-2021学年高二数学单元测试定心卷(人教B版2019选择性必修第二册)
(已下线)人教B版2019选择性必修第二册综合测试(能力提升)-2020-2021学年高二数学单元测试定心卷(人教B版2019选择性必修第二册)(已下线)专题7.3离散型随机变量的数字特征(A卷基础篇)-2020-2021学年高二下学期数学选择性必修第三册同步单元AB卷(新教材人教A版,浙江专用)(已下线)专题32 离散型随机变量的数字特征-2020-2021学年高中数学新教材人教A版选择性必修配套提升训练(已下线)专题4.4 随机变量的数字特征(A卷基础篇)-2020-2021学年高二数学选择性必修第二册同步单元AB卷(新教材人教B版)(已下线)第五课时 课后 7.3.2 离散型随机变量的方差人教A版(2019) 选修第三册 过关斩将 第七章 7.3.2 离散型随机变量的方差2023版 湘教版(2019) 选修第二册 过关斩将 第3章 3.2.4离散型随机变量的方差(已下线)7.3.2 离散型随机变量的方差(1)广西壮族自治区河池市三新学术联盟2022-2023学年高二下学期5月期中数学试题黑龙江省哈尔滨市方正县高楞高级中学校2022-2023学年高二下学期期中数学试题北师大版(2019) 选修第一册 数学奇书 第六章 概率 §3 离散型随机变量的均值与方差 3.2 离散型随机变量的方差安徽省蚌埠市蚌埠铁路中学2023-2024学年高二下学期4月月考数学试题
解题方法
5 . 某袋中装有大小相同质地均匀的5个球,其中3个黑球和2个白球.从袋中随机取出2个球,记取出白球的个数为 ,
,
(1)求 的概率即
的概率即
(2)求取出白球的数学期望 和方差
和方差
 ,
,(1)求
 的概率即
的概率即
(2)求取出白球的数学期望
 和方差
和方差
您最近一年使用:0次
2020-12-03更新
|
1000次组卷
|
9卷引用:浙江省金华市曙光学校2020-2021学年高三上学期期中数学试题
浙江省金华市曙光学校2020-2021学年高三上学期期中数学试题人教B版(2019) 选修第二册 过关检测 第四章 4.2.4 随机变量的数字特征 课时2人教A版(2019) 选修第三册 实战演练 第七章 7.3 课时练习12 离散型随机变量的方差(已下线)专题2 离散型随机变量的分布列、均值与方差-学会解题之高三数学321训练体系【2022版】(已下线)考点27 随机变量的分布列、期望与方差(核心考点讲与练)-2023年高考数学一轮复习核心考点讲与练(新高考专用)(已下线)7.3.2离散型随机变量的方差(精讲)(已下线)7.3.2 离散型随机变量的方差(1)(已下线)7.3.2离散型随机变量的方差 (分层作业)-【上好课】高二数学同步备课系列(人教A版2019选择性必修第三册)(已下线)8.2 离散型随机变量及其分布列(2)
解题方法
6 . 编号为a,b,c的三位学生随机入座编号为a,b,c的三个座位,每位学生坐一个座位,设与座位编号相同的学生的个数是 .
.
(1)求随机变量 的取值和对应的概率,并列出分布列;
的取值和对应的概率,并列出分布列;
(2)求随机变量 的数学期望及方差.
的数学期望及方差.
 .
.(1)求随机变量
 的取值和对应的概率,并列出分布列;
的取值和对应的概率,并列出分布列;(2)求随机变量
 的数学期望及方差.
的数学期望及方差.
您最近一年使用:0次
7 . 甲、乙、丙3人均以游戏的方式决定是否参加学校音乐社团、美术社团,游戏规则为:
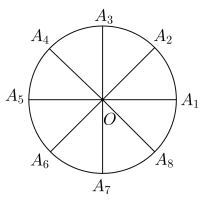
①先将一个圆8等分(如图),再将8个等分点 ,分别标注在8个相同的小球上,并将这8个小球放入一个不透明的盒子里,每个人从盒内随机摸出两个小球、然后用摸出的两个小球上标注的分点与圆心
,分别标注在8个相同的小球上,并将这8个小球放入一个不透明的盒子里,每个人从盒内随机摸出两个小球、然后用摸出的两个小球上标注的分点与圆心 构造三角形.若能构成直角三角形,则两个社团都参加;若能构成锐角三角形,则只参加美术社团;若能构成钝角三角形,则只参加音乐社团;若不能构成三角形,则两个社团都不参加.
构造三角形.若能构成直角三角形,则两个社团都参加;若能构成锐角三角形,则只参加美术社团;若能构成钝角三角形,则只参加音乐社团;若不能构成三角形,则两个社团都不参加.
②前一个同学摸出两个小球记录下结果后,把两个小球都放回盒内,下一位同学再从盒中随机摸取两个小球.
(1)求甲能参加音乐社团的概率;
(2)记甲、乙、丙3人能参加音乐社团的人数为随机变量 ,求
,求 的分布列、数学期望和方差
的分布列、数学期望和方差
①先将一个圆8等分(如图),再将8个等分点
 ,分别标注在8个相同的小球上,并将这8个小球放入一个不透明的盒子里,每个人从盒内随机摸出两个小球、然后用摸出的两个小球上标注的分点与圆心
,分别标注在8个相同的小球上,并将这8个小球放入一个不透明的盒子里,每个人从盒内随机摸出两个小球、然后用摸出的两个小球上标注的分点与圆心 构造三角形.若能构成直角三角形,则两个社团都参加;若能构成锐角三角形,则只参加美术社团;若能构成钝角三角形,则只参加音乐社团;若不能构成三角形,则两个社团都不参加.
构造三角形.若能构成直角三角形,则两个社团都参加;若能构成锐角三角形,则只参加美术社团;若能构成钝角三角形,则只参加音乐社团;若不能构成三角形,则两个社团都不参加.②前一个同学摸出两个小球记录下结果后,把两个小球都放回盒内,下一位同学再从盒中随机摸取两个小球.

(1)求甲能参加音乐社团的概率;
(2)记甲、乙、丙3人能参加音乐社团的人数为随机变量
 ,求
,求 的分布列、数学期望和方差
的分布列、数学期望和方差
您最近一年使用:0次
8 . 本小题满分12分)根据以往的经验,某工程施工期间的降水量X(单位:mm)对工期的影响如下表:
历年气象资料表明,该工程施工期间降水量X小于300,700,900的概率分别为0.3,0.7,0.9. 求:
(Ⅰ)工期延误天数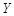 的均值与方差;
的均值与方差;
(Ⅱ)在降水量X至少是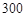 的条件下,工期延误不超过6天的概率.
的条件下,工期延误不超过6天的概率.
| 降水量X | 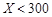 |  | 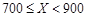 |  |
工期延误天数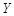 | 0 | 2 | 6 | 10 |
(Ⅰ)工期延误天数
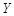 的均值与方差;
的均值与方差; (Ⅱ)在降水量X至少是
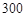 的条件下,工期延误不超过6天的概率.
的条件下,工期延误不超过6天的概率.
您最近一年使用:0次
2019-01-30更新
|
2585次组卷
|
18卷引用:2012年全国普通高等学校招生统一考试理科数学(湖北卷)
2012年全国普通高等学校招生统一考试理科数学(湖北卷)(已下线)2014高考名师推荐数学理科正态分布2015届吉林省实验中学高三上学期第五次模拟考试理科数学试卷2016届河南省南阳、周口、驻马店等六市高三第一次联考理科数学试卷2015-2016新疆哈密地区二中高二下期末考试理科数学卷内蒙古包头市第一中学2016-2017学年高二下学期期中考试数学(理)试题重庆市凤鸣山中学2019-2020学年高二下学期6月月考数学试题(已下线)专题7.3离散型随机变量的数字特征(A卷基础篇)-2020-2021学年高二下学期数学选择性必修第三册同步单元AB卷(新教材人教A版,浙江专用)(已下线)7.3.2 离散型随机变量的方差(练习)-2020-2021学年下学期高二数学同步精品课堂(新教材人教A版选择性必修第三册)人教A版(2019) 选修第三册 突围者 第七章 第三节 课时2 离散型随机变量的方差黑龙江省牡丹江市第二高级中学2022-2023学年高三上学期第二次阶段测试数学试题6.3.2离散型随机变量的方差 同步练习6.3.2离散型随机变量的方差 课时作业北师大版(2019) 选修第一册 章末检测卷(五) 概率河北省秦皇岛市卢龙县第二高级中学2023-2024学年高二下学期3月月考数学试题四川省绵阳市东辰学校2024届高三下学期第二学月考试数学(理科)试题四川省成都市金堂县淮口中学校2024届高三下学高考仿真冲刺卷(一)理科数学试题【基础卷】第7章 概率初步(续)单元测试C-沪教版(2020)选择性必修第二册





