真题
名校
1 . 等差数列 的前
的前 项和为
项和为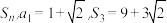 .
.
(Ⅰ)求数列 的通项
的通项 与前
与前 项和
项和 ;
;
(Ⅱ)设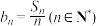 ,求证:数列
,求证:数列 中任意不同的三项都不可能成为等比数列.
中任意不同的三项都不可能成为等比数列.
 的前
的前 项和为
项和为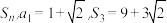 .
.(Ⅰ)求数列
 的通项
的通项 与前
与前 项和
项和 ;
;(Ⅱ)设
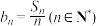 ,求证:数列
,求证:数列 中任意不同的三项都不可能成为等比数列.
中任意不同的三项都不可能成为等比数列.
您最近一年使用:0次
2019-01-30更新
|
3462次组卷
|
27卷引用:2011届江苏省无锡一中高三上学期期中考试数学试卷
(已下线)2011届江苏省无锡一中高三上学期期中考试数学试卷(已下线)2011届江苏省无锡市辅仁高级中学高三上学期期中数学卷(已下线)2011届江西省师大附中高三上学期期中考试数学理卷2015-2016学年辽宁省鞍山一中高二下期中理科数学试卷湖北省部分重点中学2017-2018学年高二下学期期中考试数学(文)试题安徽省池州市第一中学2019-2020学年高二下学期期中教学质量检测数学(理)试题2007年普通高等学校招生全国统一考试理科数学卷(福建)(已下线)2012届山东省济宁市汶上一中高三11月月考理科数学试卷(已下线)2012届江西省吉水二中高三第四次月考理科数学试卷2015-2016学年贵州遵义航天高中高二3月考文科数学试卷2015-2016湖南常德石门一中高二下第一次月考文科数学卷高中数学人教A版选修2-2 第二章 推理与证明 2.2.2 反证法(2)河南省南阳市2018-2019学年高二下学期期末考试数学(文)试题(已下线)专题11.2 直接证明与间接证明(讲)【文】-《2020年高考一轮复习讲练测》(已下线)专题11.5 第十一章 推理与证明、算法、复数(单元测试)(测)【文】-《2020年高考一轮复习讲练测》广东省华南师范大学附属中学2018-2019学年上学期高二年级期末数学试题(已下线)专题01 等差与等比数列的基本量的计算(第二篇)-备战2020年高考数学大题精做之解答题题型全覆盖沪教版(上海) 高三年级 新高考辅导与训练 第四章 数列与数学归纳法 一、等差数列与等比数列(已下线)专题12.2 直接证明与间接证明、数学归纳法(精练)-2021届高考数学(文)一轮复习讲练测(已下线)专题12.2 直接证明与间接证明、数学归纳法(精讲)-2021年高考数学(理)一轮复习讲练测(已下线)考点57 推理与证明-备战2021年高考数学(理)一轮复习考点一遍过 (已下线)考点49 推理与证明-备战2021年高考数学(文)一轮复习考点一遍过(已下线)考点43 直接证明与间接证明-备战2022年高考数学(理)一轮复习考点微专题(已下线)考点22 等差数列及其前n项和-备战2022年高考数学(理)一轮复习考点帮高中数学解题兵法 第一百讲 正难则反2007年普通高等学校招生考试数学(理)试题(福建卷)(已下线)专题6 等比数列的判断(证明)方法 微点1 定义法、等比中项法
名校
2 . (1)已知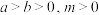 ,求证:
,求证: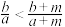 .
.
(2)已知 成等差数列,且公差
成等差数列,且公差 ,求证:
,求证: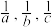 不可能成等差数列.
不可能成等差数列.
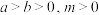 ,求证:
,求证: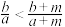 .
.(2)已知
 成等差数列,且公差
成等差数列,且公差 ,求证:
,求证: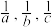 不可能成等差数列.
不可能成等差数列.
您最近一年使用:0次
2019-04-29更新
|
845次组卷
|
3卷引用:【校级联考】江苏省沭阳县2018-2019学年高二下学期期中调研测试数学试题
12-13高三上·江苏无锡·期中
名校
3 . 已知数列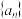 的前
的前 项和
项和 满足
满足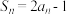 ,数列
,数列 满足
满足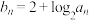 .
.
 Ⅰ
Ⅰ 求数列
求数列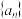 和数列
和数列 的通项公式;
的通项公式;
 Ⅱ
Ⅱ 令
令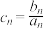 ,若
,若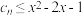 对于一切的正整数
对于一切的正整数 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
 Ⅲ
Ⅲ 数列
数列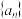 中是否存在
中是否存在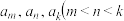 ,且
,且 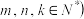 使
使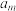 ,
, ,
,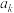 成等差数列?若存在,求出
成等差数列?若存在,求出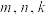 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
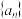 的前
的前 项和
项和 满足
满足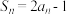 ,数列
,数列 满足
满足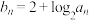 .
. Ⅰ
Ⅰ 求数列
求数列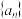 和数列
和数列 的通项公式;
的通项公式; Ⅱ
Ⅱ 令
令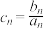 ,若
,若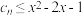 对于一切的正整数
对于一切的正整数 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; Ⅲ
Ⅲ 数列
数列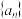 中是否存在
中是否存在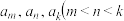 ,且
,且 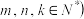 使
使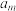 ,
, ,
,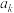 成等差数列?若存在,求出
成等差数列?若存在,求出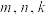 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近一年使用:0次
2018-12-12更新
|
959次组卷
|
4卷引用:2012届江苏省无锡市高三上学期期中考试数学
(已下线)2012届江苏省无锡市高三上学期期中考试数学【区级联考】北京市通州区2019届高三上学期期中考试数学(理)试题2020届北京市海淀区首都师范大学附属中学高三开学考试数学试题北京市海淀区中关村中学2022届高三上学期开学测试数学试题
10-11高二下·浙江温州·阶段练习
名校
4 . 设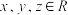 ,且
,且 ,
, ,
, ,用反证法证明:
,用反证法证明: 至少有一个大于
至少有一个大于 .
.
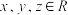 ,且
,且 ,
, ,
, ,用反证法证明:
,用反证法证明: 至少有一个大于
至少有一个大于 .
.
您最近一年使用:0次
2019-04-26更新
|
737次组卷
|
12卷引用:江苏省连云港市锦屏高级中学2018-2019学年高二下学期期中数学(理)试题
江苏省连云港市锦屏高级中学2018-2019学年高二下学期期中数学(理)试题2015-2016学年安徽省合肥一中高二下期中文科数学试卷【全国百强校】安徽省黄山市屯溪第一中学2018-2019学年高二下学期期中考试数学(文)试题陕西省商洛市洛南县2018-2019学年高二下学期期中数学(理)试题安徽省安庆市怀宁县第二中学2019-2020学年高二下学期期中线上检测数学(文)试题(已下线)2010-2011年浙江省文成中学高二下学期第一次月考文科数学(已下线)2011-2012学年浙江省嵊泗中学高二第一次月考数学试卷(7-8班)(已下线)2012年苏教版高中数学选修2-1 1.2简单的逻辑联结词练习卷高中数学人教A版选修2-2 第二章 推理与证明 2.2.2 反证法(2)【全国百强校】河南省南阳市第一中学2017-2018学年高二下学期第二次月考数学(文)试题(已下线)2019年4月14日 《每日一题》文数选修1-2(期中复习)-每周一测江西省赣州市石城县石城中学2019-2020学年高二下学期月考数学(文)试题
10-11高二下·黑龙江·期末
5 . 已知函数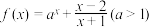 .
.
(1)证明:函数 在
在 上为增函数;
上为增函数;
(2)用反证法证明: 没有负数根.
没有负数根.
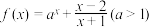 .
.(1)证明:函数
 在
在 上为增函数;
上为增函数;(2)用反证法证明:
 没有负数根.
没有负数根.
您最近一年使用:0次
2016-12-02更新
|
1492次组卷
|
16卷引用:江苏省苏州市吴中区2018-2019学年高二下学期期中数学(理)试题
江苏省苏州市吴中区2018-2019学年高二下学期期中数学(理)试题(已下线)2013-2014学年河北省唐山一中高二下学期期中考试理科数学试卷2015-2016学年甘肃省武威民勤一中高二下期中理科数学试卷安徽师范大学附属中学2020-2021学年高二下学期期中文科数学试题(已下线)庆安三中2010——2011学年度高二下学期期末考试数学(文)(已下线)2012届吉林省吉林一中高三上学期期末质量检测数学(已下线)2013届吉林省吉林一中高三上学期阶段验收数学试卷2015-2016学年河北省邢台一中高二下第一次月考理数学卷2016-2017学年江西南昌市高三新课标一轮复习一数学试卷《课时同步君》2017-2018学年高二文科数学人教选修1-2——2.2 直接证明与间接证明广州市第41中学高二第二学期数学选修1-2《推理与证明》测试题黑龙江省海林市朝鲜族中学人教版高中数学选修1-2同步练习:第二章 推理与证明单元测评(已下线)2019年3月10日 《每日一题》(文)人教选修1-2-每周一测(已下线)2019年3月21日 《每日一题》理数选修2-2-反证法(2)内蒙古集宁一中2019-2020学年高二下学期第二次月考数学(文)试题2002 年普通高等学校春季招生考试数学试题(上海卷)
名校
解题方法
6 . 已知 ,关于
,关于 的方程
的方程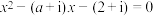 .(
.( 是虚数单位)
是虚数单位)
(1)若方程有实数根,求实数 ;
;
(2)证明:方程无纯虚数根.
 ,关于
,关于 的方程
的方程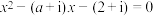 .(
.( 是虚数单位)
是虚数单位)(1)若方程有实数根,求实数
 ;
;(2)证明:方程无纯虚数根.
您最近一年使用:0次
7 . (1)已知 ,求证:
,求证: ;
;
 ,求证:
,求证: ;
;(2)若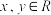 ,
, ,
,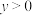 ,且
,且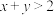 ,求证:
,求证: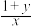 和
和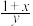 中至少有
中至少有
一个小于2.
您最近一年使用:0次
2018-05-06更新
|
543次组卷
|
3卷引用:【全国市级联考】江苏省徐州市县区2017-2018学年高二下学期期中考试数学(文科)试题
8 . (1)用分析法证明:当 ,
,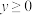 时,
时,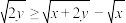 ;
;
(2)证明:对任意 ,
, ,
,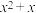 ,
,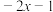 这
这 个值至少有一个不小于
个值至少有一个不小于 .
.
 ,
,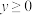 时,
时,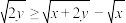 ;
;(2)证明:对任意
 ,
, ,
,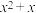 ,
,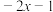 这
这 个值至少有一个不小于
个值至少有一个不小于 .
.
您最近一年使用:0次
2020-03-17更新
|
259次组卷
|
3卷引用:江苏省扬州中学2017-2018学年高二下学期期中数学(文)试题
9 . 已知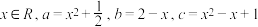 ,试用反证法证明
,试用反证法证明 中至少有一个不小于1.
中至少有一个不小于1.
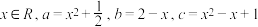 ,试用反证法证明
,试用反证法证明 中至少有一个不小于1.
中至少有一个不小于1.
您最近一年使用:0次
2021-10-18更新
|
174次组卷
|
10卷引用:2015-2016学年江苏省如东高中高二下期中数学试卷
2015-2016学年江苏省如东高中高二下期中数学试卷甘肃省庆阳市镇原中学2019-2020学年高二下学期期中考试数学(文)试题(已下线)2015高考数学(理)一轮配套特训:6-6直接证明与间接证明2014-2015年辽宁实验中学等五校高二下期末理科数学试卷2014-2015年辽宁实验中学等五校高二下期末文科数学试卷贵州省铜仁一中2016-2017学年高二下学期期末数学(文)试题(已下线)考点64 证明(讲解)-2021年高考数学复习一轮复习笔记(已下线)专题12.2 直接证明与间接证明、数学归纳法(精练)-2021届高考数学(文)一轮复习讲练测(已下线)2.2.2 间接证明-2020-2021学年高二数学(理)课时同步练(人教A版选修2-2)【巩固卷】第1章测评卷 单元测试A-沪教版(2020)必修第一册
10 . (1)已知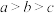 ,且
,且 ,试用分析法证明:
,试用分析法证明: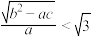 ;
;
(2)等差数列 ,
,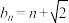 ,用反证法证明:数列
,用反证法证明:数列 中任意不同的三项都不可能成为等比数列.
中任意不同的三项都不可能成为等比数列.
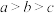 ,且
,且 ,试用分析法证明:
,试用分析法证明: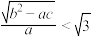 ;
;(2)等差数列
 ,
,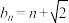 ,用反证法证明:数列
,用反证法证明:数列 中任意不同的三项都不可能成为等比数列.
中任意不同的三项都不可能成为等比数列.
您最近一年使用:0次



