北京鲁迅中学2023-2024学年七年级下学期期中数学试题
北京
七年级
期中
2024-05-16
118次
整体难度:
容易
考查范围:
数与式、方程与不等式、图形的性质、函数、图形的变化
一、单选题 添加题型下试题
A.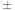 16 16 | B. | C.2 | D.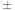  |
【知识点】 平方根
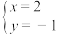 是二元一次方程
是二元一次方程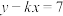 的解,则k的值是( )
的解,则k的值是( )A. | B. | C. | D. |
【知识点】 已知二元一次方程组的解求参数
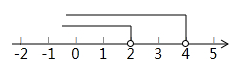
| A.x<4 | B.x<2 | C.2<x<4 | D.x>2 |
【知识点】 在数轴上表示不等式的解集解读 求不等式组的解集解读
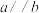 ,直角三角板的直角顶点P在直线
,直角三角板的直角顶点P在直线 上,
上, ,则
,则 为( )
为( )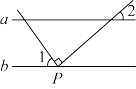
| A.24° | B.34° | C.44° | D.54° |
【知识点】 两直线平行同位角相等解读 根据平行线的性质求角的度数解读
| A.如果两条直线都与第三条直线平行,那么这两条直线也互相平行 |
| B.同旁内角相等,两直线平行 |
| C.过一点有且只有一条直线与已知直线平行 |
| D.同位角相等 |
【知识点】 根据平行线判定与性质证明 判断命题真假解读
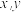 的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是
的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是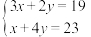 .类似的,图2所示的算筹图我们可以表述为( )
.类似的,图2所示的算筹图我们可以表述为( )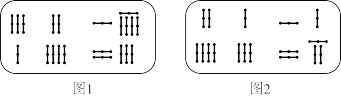
A.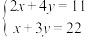 | B. | C.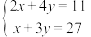 | D. |
【知识点】 古代问题(二元一次方程组的应用)
二、填空题 添加题型下试题
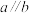 ,
, ,则
,则
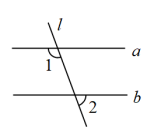
【知识点】 两直线平行内错角相等解读
【知识点】 写出命题的题设与结论解读
【知识点】 坐标与图形
 中,若将点
中,若将点 向左平移可得到点
向左平移可得到点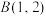 ;若将点
;若将点 向上平移可得到点
向上平移可得到点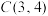 ,则点
,则点 的坐标是
的坐标是【知识点】 由平移方式确定点的坐标解读
 的正方形
的正方形 的边
的边 在数轴上,点B表示的数为1.将正方形
在数轴上,点B表示的数为1.将正方形 沿着数轴水平移动,移动后的正方形记为
沿着数轴水平移动,移动后的正方形记为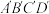 ,点A,B,C,D的对应点分别为
,点A,B,C,D的对应点分别为 ,
, ,
, ,
,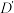 ,移动后的正方形
,移动后的正方形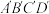 与原正方形
与原正方形 重叠部分图形的面积记为S.
重叠部分图形的面积记为S.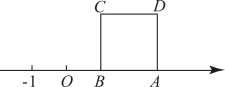
 向右移动1时,移动后的正方形
向右移动1时,移动后的正方形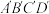 与原正方形ABCD重叠部分图形的面积为
与原正方形ABCD重叠部分图形的面积为②当时
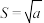 ,数轴上点
,数轴上点 表示的数是
表示的数是【知识点】 求一个数的算术平方根解读 实数与数轴解读
三、解答题 添加题型下试题
如图,
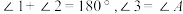 ,
,
 .
.证明:∵
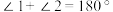 ,
,∴
 ( ).
( ).∴
 ( ).
( ).又∵
 ,
,∴ .
∴
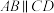 ( ).
( ).∴
 ( ).
( ).
【知识点】 根据平行线判定与性质证明
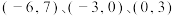 .
.
 ;
;(2)在
 中,点C经过平移后的对应点为
中,点C经过平移后的对应点为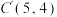 ,将
,将 作同样的平移得到
作同样的平移得到 ,画出平移后的
,画出平移后的 ,并写出点
,并写出点 的坐标;
的坐标;(3)
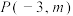 为
为 中一点,将点P向右平移4个单位后,再向下平移6个单位得到点
中一点,将点P向右平移4个单位后,再向下平移6个单位得到点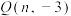 ,则
,则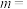 ,
, .
.
【知识点】 坐标与图形 平移(作图)解读 已知图形的平移,求点的坐标解读
(1)求这两种套装的单价分别为多少元?
(2)某校计划用1500元的资金购买这种陶制品小套装和大套装共20个作为奖品,则该校最多可以购买大套装多少个?
 ”的几何意义是:数
”的几何意义是:数 在数轴上对应的点到原点的距离,所以“
在数轴上对应的点到原点的距离,所以“ ”可理解为:数
”可理解为:数 在数轴上对应的点到原点的距离不小于
在数轴上对应的点到原点的距离不小于 ,则:
,则:①“
 ”可理解为 ;
”可理解为 ;②请列举两个符号不同的整数,使不等式“
 ”成立,列举的
”成立,列举的 的值为 和 .
的值为 和 .我们定义:形如“
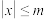 ,
,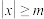 ,
,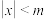 ,
,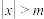 ”(
”( 为非负数)的不等式叫做绝对值不等式,能使一个绝对值不等式成立的所有未知数的值称为绝对值不等式的解集.
为非负数)的不等式叫做绝对值不等式,能使一个绝对值不等式成立的所有未知数的值称为绝对值不等式的解集.(2)【理解应用】根据绝对值的几何意义可以解一些绝对值不等式.

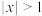 的解集是
的解集是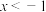 或
或 ,
,绝对值不等式
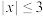 的解集是
的解集是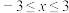 .则:
.则:①不等式
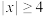 的解集是 .
的解集是 .②不等式
 的解集是 .
的解集是 .(3)【拓展应用】解不等式
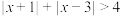 ,并画图说明.
,并画图说明.
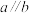 ,点A,B在直线a上,点C,D在直线b上,连接
,点A,B在直线a上,点C,D在直线b上,连接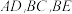 平分
平分 ,
, 平分
平分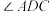 ,且
,且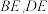 所在的直线交于点E.
所在的直线交于点E.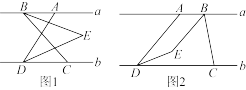
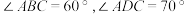 ,求
,求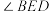 的度数;
的度数;(2)如图2,当点B在点A的右侧时,设
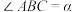 ,
,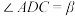 ,直接写出
,直接写出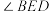 的度数(用含有
的度数(用含有 的式子表示).
的式子表示).
 中,
中,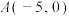 ,
,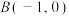 ,
,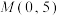 ,
, ,连接
,连接 ,以
,以 为边在
为边在 轴上方作正方形
轴上方作正方形 .
.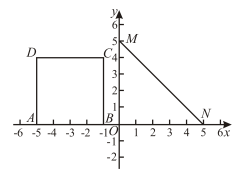
 ,
, 两点的坐标;
两点的坐标;(2)将正方形
 向右平移
向右平移 个单位长度,得到正方形
个单位长度,得到正方形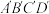 .
.①当点
 落在线段
落在线段 上时,结合图形直接写出此时
上时,结合图形直接写出此时 的值;
的值;②横、纵坐标都是整数的点叫做整点,记正方形
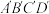 和三角形
和三角形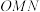 重叠的区域(不含边界)为
重叠的区域(不含边界)为 ,若区域
,若区域 内恰有
内恰有 个整点,直接写出
个整点,直接写出 的取值范围.
的取值范围.
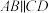 ,E、F分别在
,E、F分别在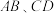 上,点G在
上,点G在 、CD之间,连接
、CD之间,连接 .
. 
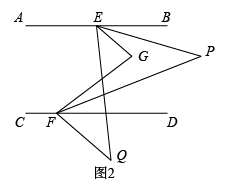
 时,
时, 平分
平分 平分
平分 ;
;①如图1,当
 时,则
时,则 ______°;
______°;②如图2,在
 的下方有一点Q,若
的下方有一点Q,若 恰好平分
恰好平分 恰好平分
恰好平分 ,求
,求 的度数;
的度数;(2)在
 的上方有一点O,若
的上方有一点O,若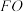 平分
平分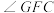 .线段
.线段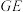 的延长线平分
的延长线平分 ,则当
,则当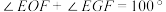 时,直接写出
时,直接写出 与
与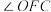 的关系.
的关系.
试卷分析
导出试卷题型(共 29题)
试卷难度
知识点分析
细目表分析
| 题号 | 难度系数 | 详细知识点 | 备注 |
| 一、单选题 | |||
| 1 | 0.85 | 平方根 | |
| 2 | 0.85 | 已知二元一次方程组的解求参数 | |
| 3 | 0.85 | 在数轴上表示不等式的解集 求不等式组的解集 | |
| 4 | 0.85 | 两直线平行同位角相等 根据平行线的性质求角的度数 | |
| 5 | 0.94 | 判断点所在的象限 | |
| 6 | 0.85 | 根据平行线判定与性质证明 判断命题真假 | |
| 7 | 0.94 | 判断点所在的象限 | |
| 8 | 0.94 | 古代问题(二元一次方程组的应用) | |
| 二、填空题 | |||
| 9 | 0.85 | 绝对值非负性 有理数的乘方运算 | |
| 10 | 0.85 | 无理数的大小估算 | |
| 11 | 0.85 | 求点到坐标轴的距离 | |
| 12 | 0.94 | 两直线平行内错角相等 | |
| 13 | 0.94 | 写出命题的题设与结论 | |
| 14 | 0.85 | 坐标与图形 | |
| 15 | 0.85 | 由平移方式确定点的坐标 | |
| 16 | 0.65 | 求一个数的算术平方根 实数与数轴 | |
| 三、解答题 | |||
| 17 | 0.85 | 实数的混合运算 | 计算题 |
| 18 | 0.65 | 利用平方根解方程 加减消元法 | 计算题 |
| 19 | 0.65 | 求一元一次不等式的解集 在数轴上表示不等式的解集 | 作图题 |
| 20 | 0.85 | 垂线段最短 点到直线的距离 画垂线 | 作图题 |
| 21 | 0.85 | 根据平行线判定与性质证明 | 证明题 |
| 22 | 0.85 | 根据平行线的性质求角的度数 | 问答题 |
| 23 | 0.65 | 求不等式组的解集 求一元一次不等式组的整数解 | 计算题 |
| 24 | 0.85 | 坐标与图形 平移(作图) 已知图形的平移,求点的坐标 | 作图题 |
| 25 | 0.65 | 分配问题(二元一次方程组的应用) 用一元一次不等式解决实际问题 | 问答题 |
| 26 | 0.94 | 绝对值的意义 绝对值的其他应用 解|x|≥a型的不等式 | 问答题 |
| 27 | 0.65 | 平行公理的应用 两直线平行内错角相等 两直线平行同旁内角互补 | 问答题 |
| 28 | 0.65 | 求不等式组的解集 写出直角坐标系中点的坐标 平移综合题(几何变换) 求点沿x轴、y轴平移后的坐标 | 问答题 |
| 29 | 0.4 | 根据平行线的性质探究角的关系 根据平行线判定与性质求角度 | 问答题 |

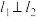 ,且在某平面直角坐标系中,x轴
,且在某平面直角坐标系中,x轴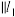 ,y轴
,y轴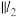 ,若点A的坐标为
,若点A的坐标为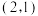 ,点B的坐标为
,点B的坐标为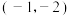 ,则点C在(
,则点C在(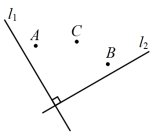
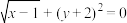 ,则
,则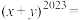
 <b,则a
<b,则a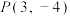 到x轴的距离为
到x轴的距离为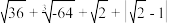
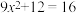

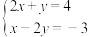
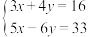
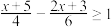 ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.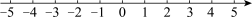
 的边
的边 上.
上.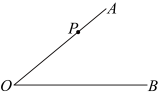
 于点C.
于点C. .
.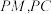 与
与 的大小关系是: (用“
的大小关系是: (用“ ”连接),判断依据: .
”连接),判断依据: .
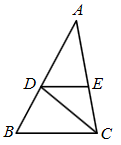
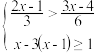 ,并求它的所有整数解.
,并求它的所有整数解.


