名校
1 . 巴黎奥运会期间,旅客人数(万人)为随机变量 ,且
,且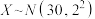 .记一天中旅客人数不少于26万人的概率为
.记一天中旅客人数不少于26万人的概率为 ,则
,则 的值约为( )
的值约为( )
(参考数据:若 ,有
,有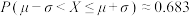 ,
,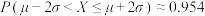 ,
,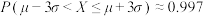 )
)
 ,且
,且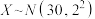 .记一天中旅客人数不少于26万人的概率为
.记一天中旅客人数不少于26万人的概率为 ,则
,则 的值约为( )
的值约为( )(参考数据:若
 ,有
,有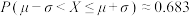 ,
,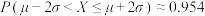 ,
,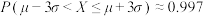 )
)| A.0.977 | B.0.9725 | C.0.954 | D.0.683 |
您最近一年使用:0次
2 . 比亚迪汽车集团监控汽车零件企业的生产过程,从汽车零件中随机抽取100件作为样本,测得质量差(零件质量与标准质量之差的绝对值)的样本数据如下表:
(1)求样本质量差的平均数 假设零件的质量差
假设零件的质量差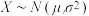 ,其中
,其中 ,用
,用 作为
作为 的近似值,求
的近似值,求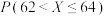 的值;
的值;
(2)已知该企业共有两条生产汽车零件的生产线,其中第1条生产线与第2条生产线生产的零件件数之比为 若第1,2条生产线的废品率分别为
若第1,2条生产线的废品率分别为 和
和 ,且这两条生产线是否产出废品是相互独立的.现从该企业生产的汽车零件中随机抽取一件.
,且这两条生产线是否产出废品是相互独立的.现从该企业生产的汽车零件中随机抽取一件.
①求抽取的零件为废品的概率;
②若抽取出的零件为废品,求该废品来自第1条生产线的概率.
参考数据:若随机变量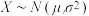 ,则
,则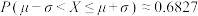 ,
,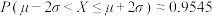 ,
,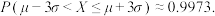
质量差(单位: | 54 | 57 | 60 | 63 | 66 |
件数(单位:件) | 5 | 21 | 46 | 25 | 3 |
 假设零件的质量差
假设零件的质量差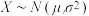 ,其中
,其中 ,用
,用 作为
作为 的近似值,求
的近似值,求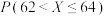 的值;
的值;(2)已知该企业共有两条生产汽车零件的生产线,其中第1条生产线与第2条生产线生产的零件件数之比为
 若第1,2条生产线的废品率分别为
若第1,2条生产线的废品率分别为 和
和 ,且这两条生产线是否产出废品是相互独立的.现从该企业生产的汽车零件中随机抽取一件.
,且这两条生产线是否产出废品是相互独立的.现从该企业生产的汽车零件中随机抽取一件.①求抽取的零件为废品的概率;
②若抽取出的零件为废品,求该废品来自第1条生产线的概率.
参考数据:若随机变量
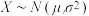 ,则
,则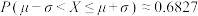 ,
,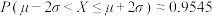 ,
,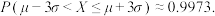
您最近一年使用:0次
解题方法
3 . 已知在某一次学情检测中,学生的数学成绩 服从正态分布
服从正态分布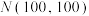 ,其中90分为及格线,120分为优秀线,则下列说法正确的是( )
,其中90分为及格线,120分为优秀线,则下列说法正确的是( )
附:随机变量 服从正态分布
服从正态分布 ,则
,则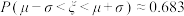 ,
,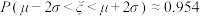 ,
,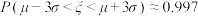
 服从正态分布
服从正态分布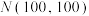 ,其中90分为及格线,120分为优秀线,则下列说法正确的是( )
,其中90分为及格线,120分为优秀线,则下列说法正确的是( )附:随机变量
 服从正态分布
服从正态分布 ,则
,则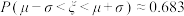 ,
,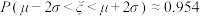 ,
,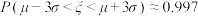
| A.学生数学成绩的期望为100 | B.学生数学成绩的标准差为100 |
| C.学生数学成绩及格率不超过0.9 | D.学生数学成绩的优秀率约等于0.023 |
您最近一年使用:0次
名校
4 . 芯片时常制造在半导体晶元表面上.某企业使用新技术对某款芯片制造工艺进行改进.部分芯片由智能检测系统进行筛选,其中部分次品芯片会被淘汰,筛选后的芯片及未经筛选的芯片进入流水线由工人进行抽样检验.记A表示事件“某芯片通过智能检测系统筛选”,B表示事件“某芯片经人工抽检后合格”.改进生产工艺后,这款芯片的某项质量指标 服从正态分布
服从正态分布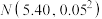 ,现从中随机抽取M个,这M个芯片中恰有m个的质量指标
,现从中随机抽取M个,这M个芯片中恰有m个的质量指标 位于区间
位于区间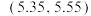 ,则下列说法正确的是( )(参考数据:
,则下列说法正确的是( )(参考数据: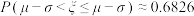 ,
,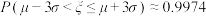 )
)
 服从正态分布
服从正态分布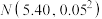 ,现从中随机抽取M个,这M个芯片中恰有m个的质量指标
,现从中随机抽取M个,这M个芯片中恰有m个的质量指标 位于区间
位于区间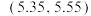 ,则下列说法正确的是( )(参考数据:
,则下列说法正确的是( )(参考数据: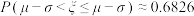 ,
,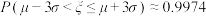 )
)A.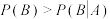 |
B.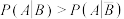 |
C.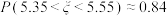 |
D. 取得最大值时,M的估计值为54 取得最大值时,M的估计值为54 |
您最近一年使用:0次
解题方法
5 . 若随机变量 ,从
,从 的取值中随机抽取
的取值中随机抽取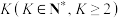 个数据,记这
个数据,记这 个数据的平均值为
个数据的平均值为 ,则随机变量
,则随机变量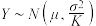 .随机变量
.随机变量 服从正态分布
服从正态分布 ,则
,则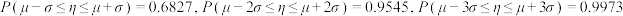 .某珠宝店出售的珍珠的直径均服从期望为15毫米,标准差为2毫米的正态分布.程女士在该珠宝店随机地挑选了16颗圆润华美的珍珠,将它串成一条璀璨夺目的项链.设这16颗珍珠的直径平均值为
.某珠宝店出售的珍珠的直径均服从期望为15毫米,标准差为2毫米的正态分布.程女士在该珠宝店随机地挑选了16颗圆润华美的珍珠,将它串成一条璀璨夺目的项链.设这16颗珍珠的直径平均值为 ,则( )
,则( )
 ,从
,从 的取值中随机抽取
的取值中随机抽取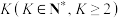 个数据,记这
个数据,记这 个数据的平均值为
个数据的平均值为 ,则随机变量
,则随机变量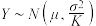 .随机变量
.随机变量 服从正态分布
服从正态分布 ,则
,则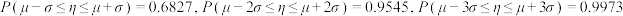 .某珠宝店出售的珍珠的直径均服从期望为15毫米,标准差为2毫米的正态分布.程女士在该珠宝店随机地挑选了16颗圆润华美的珍珠,将它串成一条璀璨夺目的项链.设这16颗珍珠的直径平均值为
.某珠宝店出售的珍珠的直径均服从期望为15毫米,标准差为2毫米的正态分布.程女士在该珠宝店随机地挑选了16颗圆润华美的珍珠,将它串成一条璀璨夺目的项链.设这16颗珍珠的直径平均值为 ,则( )
,则( )A.随机变量 的标准差为 的标准差为 | B.随机变量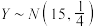 |
C.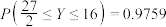 | D.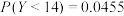 |
您最近一年使用:0次
名校
6 . 已知随机变量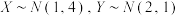 ,则下列说法正确的是( )
,则下列说法正确的是( )
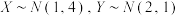 ,则下列说法正确的是( )
,则下列说法正确的是( )A.若 ,则 ,则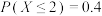 |
B.若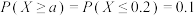 ,则 ,则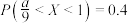 |
C.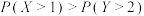 |
D.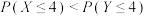 |
您最近一年使用:0次
解题方法
7 . 为加大自然生态系统和环境保护力度,加强企业对尊重自然、顺应自然、保护自然的生态文明理念,某市对化工企业的排污情况进行调查,并出台相应的整治措施.相关部门对1000家化工企业所排污水的质量及周围空气质量进行了综合检测,得分情况如频率分布直方图所示. (同一组中的数据以这组数据的中间值为代表);
(同一组中的数据以这组数据的中间值为代表);
(2)已知化工企业的得分情况 近似服从正态分布
近似服从正态分布 ,其中
,其中 ,则得分在
,则得分在 内的企业大约有多少家;
内的企业大约有多少家;
(3)按照(2)中概率分布随机抽取100家化工企业,分数不低于19分的企业有多少家时概率最大.
参考数据:若随机变量 服从正态分布
服从正态分布 ,则
,则 ,
,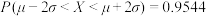 ,
,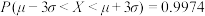 .
.
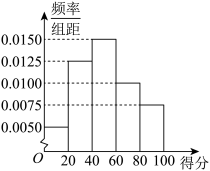
 (同一组中的数据以这组数据的中间值为代表);
(同一组中的数据以这组数据的中间值为代表);(2)已知化工企业的得分情况
 近似服从正态分布
近似服从正态分布 ,其中
,其中 ,则得分在
,则得分在 内的企业大约有多少家;
内的企业大约有多少家;(3)按照(2)中概率分布随机抽取100家化工企业,分数不低于19分的企业有多少家时概率最大.
参考数据:若随机变量
 服从正态分布
服从正态分布 ,则
,则 ,
,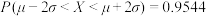 ,
,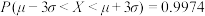 .
.
您最近一年使用:0次
解题方法
8 . “杂交水稻之父”袁隆平一生致力于杂交水稻技术的研究应用与推广,创建了超级杂交稻技术体系,为我国粮食安全、农业科学发展和世界粮食供给做出了杰出贡献,目前超级稻计划亩产已经实现1100公斤.现有某试验田,超级稻亩产量 (单位:公斤)均服从正态分布
(单位:公斤)均服从正态分布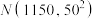 ,且
,且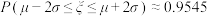 ,则1000亩试验田超级稻的亩产量在1250公斤以上的大约为
,则1000亩试验田超级稻的亩产量在1250公斤以上的大约为______ 亩(结果保留一位小数).
 (单位:公斤)均服从正态分布
(单位:公斤)均服从正态分布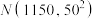 ,且
,且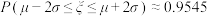 ,则1000亩试验田超级稻的亩产量在1250公斤以上的大约为
,则1000亩试验田超级稻的亩产量在1250公斤以上的大约为
您最近一年使用:0次
解题方法
9 . (多选)某市高二年级男生的身高 (单位:cm)近似服从正态分布
(单位:cm)近似服从正态分布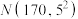 ,若随机选择一名本市高二年级的男生,则概率约为0.1359的身高范围是( )
,若随机选择一名本市高二年级的男生,则概率约为0.1359的身高范围是( )
 (单位:cm)近似服从正态分布
(单位:cm)近似服从正态分布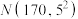 ,若随机选择一名本市高二年级的男生,则概率约为0.1359的身高范围是( )
,若随机选择一名本市高二年级的男生,则概率约为0.1359的身高范围是( )A.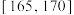 | B.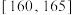 | C.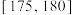 | D. |
您最近一年使用:0次
10 . 在实际生产中,通常认为服从正态分布 的随机变量
的随机变量 只取
只取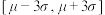 中的值,这在统计学中称为
中的值,这在统计学中称为 原则,若
原则,若 在
在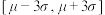 外,可以认为生产线是不正常的,已知
外,可以认为生产线是不正常的,已知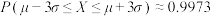 .某生产线上生产的零件长度
.某生产线上生产的零件长度 服从正态分布
服从正态分布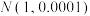 (单位:厘米),则( )
(单位:厘米),则( )
 的随机变量
的随机变量 只取
只取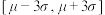 中的值,这在统计学中称为
中的值,这在统计学中称为 原则,若
原则,若 在
在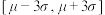 外,可以认为生产线是不正常的,已知
外,可以认为生产线是不正常的,已知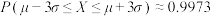 .某生产线上生产的零件长度
.某生产线上生产的零件长度 服从正态分布
服从正态分布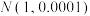 (单位:厘米),则( )
(单位:厘米),则( )A. |
B.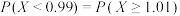 |
C.若抽检的10个样本的长度均在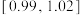 内,可以认为生产线正常 内,可以认为生产线正常 |
| D.若抽检的10个样本中有一个零件的长度为0.95,应对生产线进行检修 |
您最近一年使用:0次

 )
)

