名校
解题方法
1 . 函数 ,关于函数
,关于函数 的零点情况有下列说法:
的零点情况有下列说法:
①当 取某些值时,无零点; ②当
取某些值时,无零点; ②当 取某些值时,恰有1个零点;
取某些值时,恰有1个零点;
③当 取某些值时,恰有2个不同的零点; ④当
取某些值时,恰有2个不同的零点; ④当 取某些值时,恰有3个不同的零点.
取某些值时,恰有3个不同的零点.
则正确说法的全部序号为______ .
 ,关于函数
,关于函数 的零点情况有下列说法:
的零点情况有下列说法:①当
 取某些值时,无零点; ②当
取某些值时,无零点; ②当 取某些值时,恰有1个零点;
取某些值时,恰有1个零点;③当
 取某些值时,恰有2个不同的零点; ④当
取某些值时,恰有2个不同的零点; ④当 取某些值时,恰有3个不同的零点.
取某些值时,恰有3个不同的零点.则正确说法的全部序号为
您最近一年使用:0次
2024-03-27更新
|
260次组卷
|
2卷引用:北京市第一六六中学2023-2024学年高一上学期数学期末模拟试卷
名校
解题方法
2 . 已知函数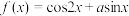 . 给出下列四个结论:①
. 给出下列四个结论:① 的最小正周期为
的最小正周期为 ;②当
;②当 时,
时, 在区间
在区间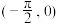 上单调递增;③若
上单调递增;③若 在区间
在区间 上的最小值为
上的最小值为 ,则
,则 ;④当
;④当 时,
时,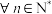 ,
, 在区间
在区间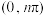 不可能存在2024个零点.其中所有正确结论的序号为
不可能存在2024个零点.其中所有正确结论的序号为_____________ .
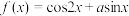 . 给出下列四个结论:①
. 给出下列四个结论:① 的最小正周期为
的最小正周期为 ;②当
;②当 时,
时, 在区间
在区间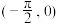 上单调递增;③若
上单调递增;③若 在区间
在区间 上的最小值为
上的最小值为 ,则
,则 ;④当
;④当 时,
时,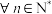 ,
, 在区间
在区间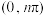 不可能存在2024个零点.其中所有正确结论的序号为
不可能存在2024个零点.其中所有正确结论的序号为
您最近一年使用:0次
解题方法
3 . 已知函数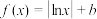 ,关于以下四个结论:
,关于以下四个结论:
①函数 的值域为
的值域为 ;
;
②当 时,方程
时,方程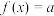 有两个不等实根;
有两个不等实根;
③当 ,
, 时,设方程
时,设方程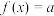 的两个根为
的两个根为 ,
, ,则
,则 为定值;
为定值;
④当 ,
, 时,设方程
时,设方程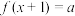 的两个根为
的两个根为 ,
, ,则
,则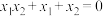 .
.
则所有正确结论的序号为_________________ .
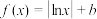 ,关于以下四个结论:
,关于以下四个结论:①函数
 的值域为
的值域为 ;
;②当
 时,方程
时,方程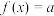 有两个不等实根;
有两个不等实根;③当
 ,
, 时,设方程
时,设方程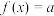 的两个根为
的两个根为 ,
, ,则
,则 为定值;
为定值;④当
 ,
, 时,设方程
时,设方程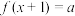 的两个根为
的两个根为 ,
, ,则
,则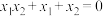 .
.则所有正确结论的序号为
您最近一年使用:0次



