名校
解题方法
1 . 中国建设新的芯片工厂的速度处于世界前列,这是朝着提高半导体自给率目标迈出的重要一步.根据国际半导体产业协会(SEMI)的数据,在截至2024年的4年里,中国计划建设31家大型半导体工厂.某公司打算在2023年度建设某型芯片的生产线,建设该生产线的成本为300万元,若该型芯片生产线在2024年产出 万枚芯片,还需要投入物料及人工等成本
万枚芯片,还需要投入物料及人工等成本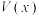 (单位:万元),已知当
(单位:万元),已知当 时,
时, ;当
;当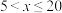 时,
时,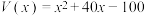 ;当
;当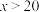 时,
时,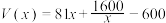 ,已知生产的该型芯片都能以每枚80元的价格售出.
,已知生产的该型芯片都能以每枚80元的价格售出.
(1)已知2024年该型芯片生产线的利润为 (单位:万元),试求出
(单位:万元),试求出 的函数解析式.
的函数解析式.
(2)请你为该型芯片的生产线的产量做一个计划,使得2024年该型芯片的生产线所获利润最大,并预测最大利润.
 万枚芯片,还需要投入物料及人工等成本
万枚芯片,还需要投入物料及人工等成本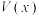 (单位:万元),已知当
(单位:万元),已知当 时,
时, ;当
;当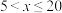 时,
时,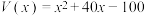 ;当
;当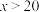 时,
时,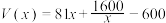 ,已知生产的该型芯片都能以每枚80元的价格售出.
,已知生产的该型芯片都能以每枚80元的价格售出.(1)已知2024年该型芯片生产线的利润为
 (单位:万元),试求出
(单位:万元),试求出 的函数解析式.
的函数解析式.(2)请你为该型芯片的生产线的产量做一个计划,使得2024年该型芯片的生产线所获利润最大,并预测最大利润.
您最近一年使用:0次
2024-02-20更新
|
1280次组卷
|
9卷引用:河南省豫东四校2022-2023学年高一下学期第一次联考(1月)数学试卷
河南省豫东四校2022-2023学年高一下学期第一次联考(1月)数学试卷上海市复旦大学附属中学2023-2024学年高一上学期期中测试数学试卷云南省大理州下关第一中学2023-2024学年高一下学期3月段考(一)数学试题四川省眉山市两校(丹棱中学校、青神中学校)2023-2024学年高一下学期4月期中考试数学试题(已下线)第08讲 基本不等式(2)-【暑假自学课】(苏教版2019必修第一册)江苏省连云港市新海高级中学2024-2025学年高一上学期开学质量检测数学试题山东省滕州市第一中学2024-2025学年高一上学期10月月考数学试卷福建省泉州市安溪沼涛中学2024-2025学年高一上学期第一次质量检测数学试卷广东省广州市第六中学2024-2025学年高一上学期期中考试数学试卷
名校
解题方法
2 . 天气渐冷,某电子设备生产企业准备投入生产“暖手宝”.预估生产线建设等固定成本投入为100万,每生产 万个还需投入生产成本
万个还需投入生产成本 万元,且据测算
万元,且据测算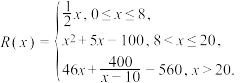 若该公司年内共生产该款“暖手宝”
若该公司年内共生产该款“暖手宝” 万只,每只售价45元并能全部销售完.
万只,每只售价45元并能全部销售完.
(1)求出利润 (万元)关于年产量
(万元)关于年产量 万个的函数解析式
万个的函数解析式 ;
;
(2)当产量至少为多少个时,该公司在该款“暖手宝”生产销售中才能收回成本;
(3)当产量达到多少万个时,该公司所获得的利润最大?并求出最大利润.
 万个还需投入生产成本
万个还需投入生产成本 万元,且据测算
万元,且据测算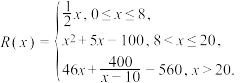 若该公司年内共生产该款“暖手宝”
若该公司年内共生产该款“暖手宝” 万只,每只售价45元并能全部销售完.
万只,每只售价45元并能全部销售完.(1)求出利润
 (万元)关于年产量
(万元)关于年产量 万个的函数解析式
万个的函数解析式 ;
;(2)当产量至少为多少个时,该公司在该款“暖手宝”生产销售中才能收回成本;
(3)当产量达到多少万个时,该公司所获得的利润最大?并求出最大利润.
您最近一年使用:0次
2023-11-26更新
|
386次组卷
|
2卷引用:浙江省台金七校联盟2023-2024学年高一上学期11月期中联考数学试题
名校
解题方法
3 . 民族要复兴,乡村要振兴,合作社助力乡村产业振兴,农民专业合作社已成为新型农业经营主体和现代农业建设的中坚力量,为实施乡村振兴战略作出了巨大的贡献.某农民专业合作社为某品牌服装进行代加工,已知代加工该品牌服装每年需投入固定成本30万元,每代加工 万件该品牌服装,需另投入
万件该品牌服装,需另投入 万元,且
万元,且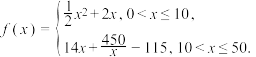 根据市场行情,该农民专业合作社为这一品牌服装每代加工一件服装,可获得12元的代加工费.
根据市场行情,该农民专业合作社为这一品牌服装每代加工一件服装,可获得12元的代加工费.
(1)求该农民专业合作社为这一品牌服装代加工费的年利润y(单位:万元)关于年代加工量x(单位:万件)的函数解析式.
(2)当年代加工量为多少万件时,该农民专业合作社为这一品牌服装代加工费的年利润最大?并求出年利润的最大值.
 万件该品牌服装,需另投入
万件该品牌服装,需另投入 万元,且
万元,且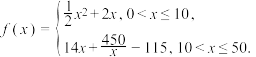 根据市场行情,该农民专业合作社为这一品牌服装每代加工一件服装,可获得12元的代加工费.
根据市场行情,该农民专业合作社为这一品牌服装每代加工一件服装,可获得12元的代加工费.(1)求该农民专业合作社为这一品牌服装代加工费的年利润y(单位:万元)关于年代加工量x(单位:万件)的函数解析式.
(2)当年代加工量为多少万件时,该农民专业合作社为这一品牌服装代加工费的年利润最大?并求出年利润的最大值.
您最近一年使用:0次
2023-07-27更新
|
1169次组卷
|
10卷引用:江西省南昌市部分学校2022-2023学年高二下学期6月期末数学试题
江西省南昌市部分学校2022-2023学年高二下学期6月期末数学试题辽宁省县级重点高中联合体2022-2023学年高二下学期期末考试数学试题湖南省长沙市长郡中学2023-2024学年高二上学期入学考试(暑假作业检测)数学试题广东省深圳市南头中学2024届高三上学期第一次月考数学试题福建省宁德第一中学2024届高三第一次考试数学试题广东省四校联考2024届高三上学期9月月考数学试题湖南省邵阳市第二中学2023-2024学年高一上学期期中数学试题(已下线)高一上学期期末复习【第三章 函数的概念与性质】十大题型归纳(基础篇)-举一反三系列(已下线)8.2 函数与数学模型(六大题型)-【帮课堂】(苏教版2019必修第一册)广东省肇庆市加美学校2024届高三上学期10月月考数学试题
4 . 病毒感染是指病毒通过多种途径侵入机体,并在易感的宿主细胞中增殖的过程.如果一个宿主感染了病毒并且在刚出现不良反应时就对症下药,在用药 小时后病毒的数量为
小时后病毒的数量为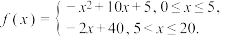 (细菌个数的单位:百个)
(细菌个数的单位:百个)
(1)求曲线 点在
点在 处的切线方程;
处的切线方程;
(2)求细菌数量超过14(百个)的时间段.
 小时后病毒的数量为
小时后病毒的数量为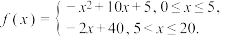 (细菌个数的单位:百个)
(细菌个数的单位:百个)(1)求曲线
 点在
点在 处的切线方程;
处的切线方程;(2)求细菌数量超过14(百个)的时间段.
您最近一年使用:0次
2023-07-14更新
|
181次组卷
|
2卷引用:山东省聊城市2022-2023学年高二下学期期末数学试题
2023·全国·模拟预测
5 . 2022年9月20日是第34个“全国爱牙日”,宣传主题是“口腔健康,全身健康”.要想口腔健康,良好的刷牙习惯不可少,牙刷的质量也是至关重要的,与手动牙刷相比较,电动牙刷的清洁力更高,刷牙效果更好.某医生计划购买某种品牌的电动牙刷,预计使用寿命为5年,该电动牙刷的刷头在使用过程中需要更换.若购买该品牌电动牙刷的同时购买刷头,则每个刷头20元;若单独购买刷头,则每个刷头30元.某经销商随机调查了使用该品牌电动牙刷的100名医生在5年使用期内更换刷头的个数,得到下表:
用 (
( )表示1个该品牌电动牙刷在5年使用期内需更换刷头的个数,
)表示1个该品牌电动牙刷在5年使用期内需更换刷头的个数, 表示购买刷头的费用(单位:元).
表示购买刷头的费用(单位:元).
(1)求这100名医生在5年使用期内更换刷头的个数的中位数;
(2)若购买1个该品牌电动牙刷的同时购买了18个刷头,求 关于
关于 的函数解析式;
的函数解析式;
(3)假设这100名医生购买1个该品牌电动牙刷的同时都购买了17个刷头或18个刷头,分别计算这100名医生购买刷头费用的平均数,以此作为决策依据,判断购买1个该品牌电动牙刷的同时应购买17个刷头还是18个刷头.
更换刷头的个数 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 8 | 8 | 10 | 24 | 28 | 12 | 10 |
 (
( )表示1个该品牌电动牙刷在5年使用期内需更换刷头的个数,
)表示1个该品牌电动牙刷在5年使用期内需更换刷头的个数, 表示购买刷头的费用(单位:元).
表示购买刷头的费用(单位:元).(1)求这100名医生在5年使用期内更换刷头的个数的中位数;
(2)若购买1个该品牌电动牙刷的同时购买了18个刷头,求
 关于
关于 的函数解析式;
的函数解析式;(3)假设这100名医生购买1个该品牌电动牙刷的同时都购买了17个刷头或18个刷头,分别计算这100名医生购买刷头费用的平均数,以此作为决策依据,判断购买1个该品牌电动牙刷的同时应购买17个刷头还是18个刷头.
您最近一年使用:0次
解题方法
6 . 受疫情影响 年下半年多地又陆续开启“线上教学模式”.某机构经过调查发现学生的上课注意力指数
年下半年多地又陆续开启“线上教学模式”.某机构经过调查发现学生的上课注意力指数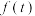 与听课时间
与听课时间 (单位:
(单位: )之间满足如下关系:
)之间满足如下关系:
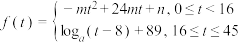 ,其中
,其中 ,
, 且
且 .已知
.已知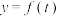 在区间
在区间 上的最大值为
上的最大值为 ,最小值为
,最小值为 ,且
,且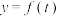 的图象过点
的图象过点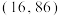 .
.
(1)试求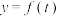 的函数关系式;
的函数关系式;
(2)若注意力指数大于等于 时听课效果最佳,则教师在什么时间段内安排核心内容,能使学生听课效果最佳?请说明理由.
时听课效果最佳,则教师在什么时间段内安排核心内容,能使学生听课效果最佳?请说明理由.
 年下半年多地又陆续开启“线上教学模式”.某机构经过调查发现学生的上课注意力指数
年下半年多地又陆续开启“线上教学模式”.某机构经过调查发现学生的上课注意力指数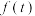 与听课时间
与听课时间 (单位:
(单位: )之间满足如下关系:
)之间满足如下关系: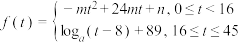 ,其中
,其中 ,
, 且
且 .已知
.已知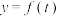 在区间
在区间 上的最大值为
上的最大值为 ,最小值为
,最小值为 ,且
,且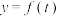 的图象过点
的图象过点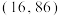 .
.(1)试求
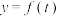 的函数关系式;
的函数关系式;(2)若注意力指数大于等于
 时听课效果最佳,则教师在什么时间段内安排核心内容,能使学生听课效果最佳?请说明理由.
时听课效果最佳,则教师在什么时间段内安排核心内容,能使学生听课效果最佳?请说明理由.
您最近一年使用:0次
2023-02-10更新
|
362次组卷
|
3卷引用:山东省潍坊市2022-2023学年高一上学期期末考试数学试题
名校
解题方法
7 . 地铁作为城市交通的重要组成部分,以其准时、高效的优点广受青睐.某城市新修建了一条地铁线路,经调研测算,每辆列车的载客量h(单位:人)与发车时间间隔t(单位:分钟,且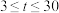 )有关:当发车时间间隔
)有关:当发车时间间隔达到或超过 15分钟时,列车均为满载状态,载客量为1700人;当发车时间间隔不超过 15分钟时,地铁载客量h与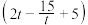 成正比.假设每辆列车的日均车票收入
成正比.假设每辆列车的日均车票收入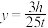 (单位:万元).
(单位:万元).
(1)求y关于t的函数表达式;
(2)当发车时间间隔为何值时,每辆列车的日均车票收入最大?并求出该最大值.
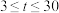 )有关:当发车时间间隔
)有关:当发车时间间隔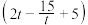 成正比.假设每辆列车的日均车票收入
成正比.假设每辆列车的日均车票收入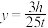 (单位:万元).
(单位:万元).(1)求y关于t的函数表达式;
(2)当发车时间间隔为何值时,每辆列车的日均车票收入最大?并求出该最大值.
您最近一年使用:0次
2023-02-10更新
|
379次组卷
|
4卷引用:山东省烟台市2022-2023学年高一上学期期末数学试题
山东省烟台市2022-2023学年高一上学期期末数学试题(已下线)模块四 专题6 大题分类练(函数的概念与性质)基础夯实练(人教A)山东省临沂市第十八中学2023-2024学年高一上学期期末模拟数学试题(四)山东省潍坊市第一中学2023-2024学年高一下学期清明后摸底考试(4月月考)数学试题
名校
8 . 2022年夏天,重庆遭遇了极端高温天气,某空调厂家加大力度促进生产.生产某款空调的固定成本是1000万元,每生产 千台,需另投入成本
千台,需另投入成本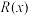 (单位:万元),
(单位:万元), ,生产的空调能全部销售完,每台空调平均售价5千元.
,生产的空调能全部销售完,每台空调平均售价5千元.
(1)写出年利润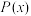 (单位:万元)关于年产量x(单位:千台)的关系式;
(单位:万元)关于年产量x(单位:千台)的关系式;
(2)当年产量为多少千台时,这款空调的年利润最大?最大为多少?
 千台,需另投入成本
千台,需另投入成本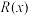 (单位:万元),
(单位:万元), ,生产的空调能全部销售完,每台空调平均售价5千元.
,生产的空调能全部销售完,每台空调平均售价5千元.(1)写出年利润
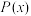 (单位:万元)关于年产量x(单位:千台)的关系式;
(单位:万元)关于年产量x(单位:千台)的关系式;(2)当年产量为多少千台时,这款空调的年利润最大?最大为多少?
您最近一年使用:0次
2023-02-03更新
|
867次组卷
|
4卷引用:重庆市巴蜀中学校2022-2023学年高一上学期期末数学试题
名校
解题方法
9 . 近几年,极端天气的天数较往年增加了许多,环境的保护越来越受到民众的关注,企业的节能减排被国家纳入了发展纲要中,这也为检测环境的仪器企业带来了发展机遇.某仪器公司的生产环境检测仪全年需要固定投入500万元,每生产x百台检测仪器还需要投入y万元,其中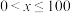 ,
,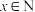 ,且
,且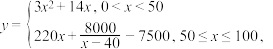 每台检测仪售价2万元,且每年生产的检测仪器都可以售完.
每台检测仪售价2万元,且每年生产的检测仪器都可以售完.
(1)求该公司生产的环境检测仪的年利润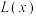 (万元)关于年产量x(百台)的函数关系式;
(万元)关于年产量x(百台)的函数关系式;
(2)求该公司生产的环境检测仪年利润的最大值.
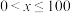 ,
,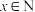 ,且
,且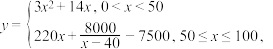 每台检测仪售价2万元,且每年生产的检测仪器都可以售完.
每台检测仪售价2万元,且每年生产的检测仪器都可以售完.(1)求该公司生产的环境检测仪的年利润
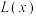 (万元)关于年产量x(百台)的函数关系式;
(万元)关于年产量x(百台)的函数关系式;(2)求该公司生产的环境检测仪年利润的最大值.
您最近一年使用:0次
2022-11-10更新
|
677次组卷
|
10卷引用:辽宁省铁岭市昌图县第一高级中学2022-2023学年高二下学期期末考试数学试题
辽宁省铁岭市昌图县第一高级中学2022-2023学年高二下学期期末考试数学试题河北省沧州市献县实验中学2023-2024学年高一上学期期中数学试题吉林省白山市抚松县第一中学2023-2024学年高一上学期11月月考数学试题陕西省多校2022-2023学年高一上学期第二次选科调考数学试题河北省2022-2023学年高一上学期期中数学试题吉林省部分名校2022-2023学年高一上学期期中考试数学试题河北省衡水市第十三中学2022-2023学年高一上学期11月质检(二)数学试题陕西省榆林市横山区实验中学等4校2022-2023学年高一上学期期中文科数学试题辽宁省抚顺市六校协作体2022-2023学年高一上学期期中考试数学试题吉林省吉林市第二中学2024-2025学年高一上学期期中考试数学试题
名校
10 . 党的十八大以来,精准扶贫取得了历史性成就,其中产业扶贫是扶贫工作的一项重要举措,长沙某驻村扶贫小组在湘西某贫困村实施产业扶贫,计划帮助该村进行猕猴桃的种植与销售,为了迎合大众需求,提高销售量,将以装盒售卖的方式销售.经市场调研,若要提高销售量,则猕猴桃的售价需要相应的降低,已知猕猴桃的种植与包装成本为24元/盒,且每万盒猕猴桃的销售收入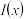 (单位:万元)与售价量x(单位:万盒)之间满足关系式
(单位:万元)与售价量x(单位:万盒)之间满足关系式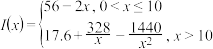 .
.
(1)写出利润 (单位:万元)关于销售量x(单位:万盒)的关系式;(利润=销售收入-成本)
(单位:万元)关于销售量x(单位:万盒)的关系式;(利润=销售收入-成本)
(2)当销售量为多少万盒时,该村能够获得最大利润?此时最大利润是多少?
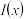 (单位:万元)与售价量x(单位:万盒)之间满足关系式
(单位:万元)与售价量x(单位:万盒)之间满足关系式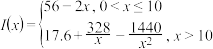 .
.(1)写出利润
 (单位:万元)关于销售量x(单位:万盒)的关系式;(利润=销售收入-成本)
(单位:万元)关于销售量x(单位:万盒)的关系式;(利润=销售收入-成本)(2)当销售量为多少万盒时,该村能够获得最大利润?此时最大利润是多少?
您最近一年使用:0次
2022-10-09更新
|
630次组卷
|
4卷引用:四川省眉山北外附属东坡外国语学校2022-2023学年高一下学期开学考试数学试题
四川省眉山北外附属东坡外国语学校2022-2023学年高一下学期开学考试数学试题湖南师范大学附属中学2022-2023学年高一上学期第一次大练习数学试题(已下线)专题3.4 函数的应用(一)(3类必考点)-2022-2023学年高一数学必考点分类集训系列(人教A版2019必修第一册)山东省泰安第一中学2022-2023学年高一上学期期中数学试题



