1 . 已知实数 满足:①
满足:①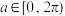 ;②存在实数
;②存在实数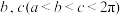 ,使得
,使得 ,
, ,
, 是等差数列,
是等差数列,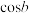 ,
, ,
, 也是等差数列.则实数
也是等差数列.则实数 的取值范围是
的取值范围是________ .
 满足:①
满足:①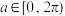 ;②存在实数
;②存在实数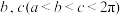 ,使得
,使得 ,
, ,
, 是等差数列,
是等差数列,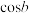 ,
, ,
, 也是等差数列.则实数
也是等差数列.则实数 的取值范围是
的取值范围是
您最近一年使用:0次
2 . 设 是定义域为
是定义域为 的函数,如果对任意的
的函数,如果对任意的 、
、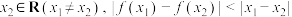 均成立, 则称
均成立, 则称 是“平缓函数”.
是“平缓函数”.
(1)若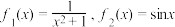 , 试判断
, 试判断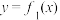 和
和 是否为“平缓函数” ? 并说明理由; (参考公式:
是否为“平缓函数” ? 并说明理由; (参考公式: 时,
时,  恒成立)
恒成立)
(2)若函数 是“平缓函数”, 且
是“平缓函数”, 且 是以 1为周期的周期函数, 证明:对任意的
是以 1为周期的周期函数, 证明:对任意的 、
、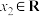 , 均有
, 均有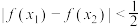 ;
;
(3)设 为定义在
为定义在 上函数, 且存在正常数
上函数, 且存在正常数 使得函数
使得函数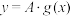 为“平缓函数”. 现定义数列
为“平缓函数”. 现定义数列 满足:
满足: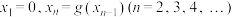 , 试证明:对任意的正整数
, 试证明:对任意的正整数 .
.
 是定义域为
是定义域为 的函数,如果对任意的
的函数,如果对任意的 、
、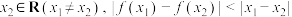 均成立, 则称
均成立, 则称 是“平缓函数”.
是“平缓函数”.(1)若
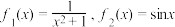 , 试判断
, 试判断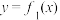 和
和 是否为“平缓函数” ? 并说明理由; (参考公式:
是否为“平缓函数” ? 并说明理由; (参考公式: 时,
时,  恒成立)
恒成立)(2)若函数
 是“平缓函数”, 且
是“平缓函数”, 且 是以 1为周期的周期函数, 证明:对任意的
是以 1为周期的周期函数, 证明:对任意的 、
、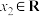 , 均有
, 均有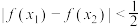 ;
;(3)设
 为定义在
为定义在 上函数, 且存在正常数
上函数, 且存在正常数 使得函数
使得函数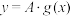 为“平缓函数”. 现定义数列
为“平缓函数”. 现定义数列 满足:
满足: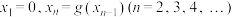 , 试证明:对任意的正整数
, 试证明:对任意的正整数 .
.
您最近一年使用:0次
名校
3 . 已知等差数列 的公差
的公差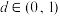 ,且
,且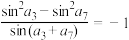 ,若
,若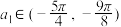 时,则数列
时,则数列 的前
的前 项和为
项和为 取得最小值时
取得最小值时 的值为
的值为_________ .
 的公差
的公差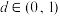 ,且
,且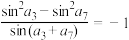 ,若
,若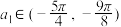 时,则数列
时,则数列 的前
的前 项和为
项和为 取得最小值时
取得最小值时 的值为
的值为
您最近一年使用:0次
4 . 已知 是定义在
是定义在 上的函数,如果存在常数
上的函数,如果存在常数 ,对区间
,对区间 的任意划分:
的任意划分: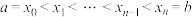 ,和式
,和式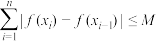 恒成立,则称
恒成立,则称 为
为 上的“绝对差有界函数”。注:
上的“绝对差有界函数”。注: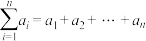 。
。
(1)证明函数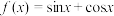 在
在 上是“绝对差有界函数”。
上是“绝对差有界函数”。
(2)证明函数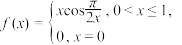 不是
不是 上的“绝对差有界函数”。
上的“绝对差有界函数”。
(3)记集合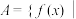 存在常数
存在常数 ,对任意的
,对任意的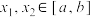 ,有
,有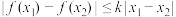 成立
成立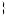 ,证明集合
,证明集合 中的任意函数
中的任意函数 为“绝对差有界函数”,并判断
为“绝对差有界函数”,并判断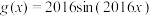 是否在集合
是否在集合 中,如果在,请证明并求
中,如果在,请证明并求 的最小值;如果不在,请说明理由。
的最小值;如果不在,请说明理由。
 是定义在
是定义在 上的函数,如果存在常数
上的函数,如果存在常数 ,对区间
,对区间 的任意划分:
的任意划分: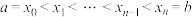 ,和式
,和式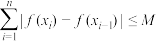 恒成立,则称
恒成立,则称 为
为 上的“绝对差有界函数”。注:
上的“绝对差有界函数”。注: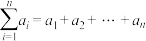 。
。(1)证明函数
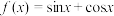 在
在 上是“绝对差有界函数”。
上是“绝对差有界函数”。(2)证明函数
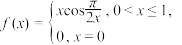 不是
不是 上的“绝对差有界函数”。
上的“绝对差有界函数”。(3)记集合
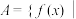 存在常数
存在常数 ,对任意的
,对任意的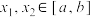 ,有
,有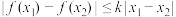 成立
成立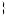 ,证明集合
,证明集合 中的任意函数
中的任意函数 为“绝对差有界函数”,并判断
为“绝对差有界函数”,并判断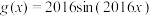 是否在集合
是否在集合 中,如果在,请证明并求
中,如果在,请证明并求 的最小值;如果不在,请说明理由。
的最小值;如果不在,请说明理由。
您最近一年使用:0次



