名校
1 . 《中国制造2025》是中国实施制造强国战略第一个十年的行动纲领,制造业是国民经济的主体,是立国之本、兴国之器、强国之基发展制造业的基本方针为质量为先,坚持把质量作为建设制造强国的生命线.某电子产品制造企业为了提升生产效率,对现有的一条电子产品生产线进行技术升级改造,为了分析改造的效果,该企业质检人员从该条生产线所生产的电子产品中随机抽取了1000件,检测产品的某项质量指标值,根据检测数据得到下表(单位:件).
(1)估计这组样本的质量指标值的平均数 和方差
和方差 (同一组中的数据用该组区间中点值作代表);
(同一组中的数据用该组区间中点值作代表);
(2)设 表示不大于
表示不大于 的最大整数,
的最大整数, 表示不小于
表示不小于 的最小整数,
的最小整数, 精确到个位,
精确到个位,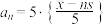 ,
,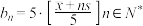 ,根据检验标准,技术升级改造后,若质量指标值有65%落在
,根据检验标准,技术升级改造后,若质量指标值有65%落在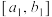 内,则可以判断技术改造后的产品质量初级稳定;若有95%落在
内,则可以判断技术改造后的产品质量初级稳定;若有95%落在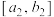 内,则可以判断技术改造后的产品质量稳定,可认为生产线技术改造成功.请问:根据样本数据估计,是否可以判定生产线的技术改造是成功的?
内,则可以判断技术改造后的产品质量稳定,可认为生产线技术改造成功.请问:根据样本数据估计,是否可以判定生产线的技术改造是成功的?
(3)为了检测技术人员的业务知识,该企业对两名业务人员进行知识考核竞赛,规则如下:在初赛中有两轮答题:第一轮从 类的5个问题中任选两题作答,若两题都答对,则得20分,否则得0分;第二轮从
类的5个问题中任选两题作答,若两题都答对,则得20分,否则得0分;第二轮从 类的4个问题中任选两题依次作答,每答对一题得20分,答错得0分.若两轮总得分不低于40分,则晋级复赛.甲和乙同时参赛,已知在
类的4个问题中任选两题依次作答,每答对一题得20分,答错得0分.若两轮总得分不低于40分,则晋级复赛.甲和乙同时参赛,已知在 类的5个问题中,甲只能答对4个问题,在
类的5个问题中,甲只能答对4个问题,在 类的4个问题中,甲答对的概率都为0.4;乙答对每个问题的概率都为0.6.甲、乙回答任一问题正确与否互不影响.
类的4个问题中,甲答对的概率都为0.4;乙答对每个问题的概率都为0.6.甲、乙回答任一问题正确与否互不影响.
(ⅰ)求甲在第一轮比赛中得0分的概率;
(ⅱ)以晋级复赛的概率大小为依据,甲和乙谁更容易晋级复赛?
质量指标 |
|
|
|
|
|
|
|
产品 | 60 | 100 | 160 | 300 | 200 | 100 | 80 |
 和方差
和方差 (同一组中的数据用该组区间中点值作代表);
(同一组中的数据用该组区间中点值作代表);(2)设
 表示不大于
表示不大于 的最大整数,
的最大整数, 表示不小于
表示不小于 的最小整数,
的最小整数, 精确到个位,
精确到个位,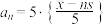 ,
,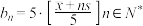 ,根据检验标准,技术升级改造后,若质量指标值有65%落在
,根据检验标准,技术升级改造后,若质量指标值有65%落在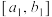 内,则可以判断技术改造后的产品质量初级稳定;若有95%落在
内,则可以判断技术改造后的产品质量初级稳定;若有95%落在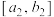 内,则可以判断技术改造后的产品质量稳定,可认为生产线技术改造成功.请问:根据样本数据估计,是否可以判定生产线的技术改造是成功的?
内,则可以判断技术改造后的产品质量稳定,可认为生产线技术改造成功.请问:根据样本数据估计,是否可以判定生产线的技术改造是成功的?(3)为了检测技术人员的业务知识,该企业对两名业务人员进行知识考核竞赛,规则如下:在初赛中有两轮答题:第一轮从
 类的5个问题中任选两题作答,若两题都答对,则得20分,否则得0分;第二轮从
类的5个问题中任选两题作答,若两题都答对,则得20分,否则得0分;第二轮从 类的4个问题中任选两题依次作答,每答对一题得20分,答错得0分.若两轮总得分不低于40分,则晋级复赛.甲和乙同时参赛,已知在
类的4个问题中任选两题依次作答,每答对一题得20分,答错得0分.若两轮总得分不低于40分,则晋级复赛.甲和乙同时参赛,已知在 类的5个问题中,甲只能答对4个问题,在
类的5个问题中,甲只能答对4个问题,在 类的4个问题中,甲答对的概率都为0.4;乙答对每个问题的概率都为0.6.甲、乙回答任一问题正确与否互不影响.
类的4个问题中,甲答对的概率都为0.4;乙答对每个问题的概率都为0.6.甲、乙回答任一问题正确与否互不影响.(ⅰ)求甲在第一轮比赛中得0分的概率;
(ⅱ)以晋级复赛的概率大小为依据,甲和乙谁更容易晋级复赛?
您最近一年使用:0次
名校
解题方法
2 . 根据以往的统计资料,甲、乙两运动员在比赛中的得分情况统计如下:
甲
乙
现有一场比赛,派哪位运动员参加比较好?请写出你的决定,并说明理由.
甲
X | 0 | 1 | 2 |
P | 0.1 | 0.8 | 0.1 |
X | 0 | 1 | 2 |
P | 0.4 | 0.2 | 0.4 |
您最近一年使用:0次
2024-05-04更新
|
236次组卷
|
3卷引用:北京市第三十五中学2023-2024学年高二下学期期中考试数学试题
北京市第三十五中学2023-2024学年高二下学期期中考试数学试题吉林省长春市第二中学2023-2024学年高二下学期5月期中考试数学试题(已下线)第三章 随机变量及其分布列 专题二 随机变量的方差 微点2 随机变量的方差综合训练【基础版】
名校
3 . (1)已知甲乙两名同学的某次体育项目测试成绩分别为:甲:10,13,12,14,16.乙:13,14,12,12,14.求甲乙两人成绩的平均数与方差,比较谁的成绩更稳定.
(2)某学校为了调查学生的学习情况,现用分层抽样的方法抽取样本,若样本中有20名男生,30名女生,且男生的平均成绩为70分,方差为4,女生的平均成绩为80分,方差为6,求所抽取样本的方差.
(2)某学校为了调查学生的学习情况,现用分层抽样的方法抽取样本,若样本中有20名男生,30名女生,且男生的平均成绩为70分,方差为4,女生的平均成绩为80分,方差为6,求所抽取样本的方差.
您最近一年使用:0次
名校
4 . 某稻谷试验田试种了 ,
, 两个品种的水稻各10亩,并在稻谷成熟后统计了这20亩地的稻谷产量如下表,记
两个品种的水稻各10亩,并在稻谷成熟后统计了这20亩地的稻谷产量如下表,记 ,
, 两个品种各10亩产量的平均数分别为
两个品种各10亩产量的平均数分别为 和
和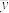 ,方差分别为
,方差分别为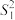 和
和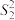 .
.
(1)分别求这两个品种产量的极差和中位数;
(2)求 ,
,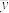 ,
,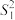 ,
,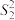 ;
;
(3)依据以上计算结果进行分析,推广种植 品种还是
品种还是 品种水稻更合适.
品种水稻更合适.
 ,
, 两个品种的水稻各10亩,并在稻谷成熟后统计了这20亩地的稻谷产量如下表,记
两个品种的水稻各10亩,并在稻谷成熟后统计了这20亩地的稻谷产量如下表,记 ,
, 两个品种各10亩产量的平均数分别为
两个品种各10亩产量的平均数分别为 和
和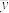 ,方差分别为
,方差分别为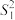 和
和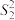 .
.
| 60 | 63 | 50 | 76 | 71 | 85 | 75 | 63 | 63 | 64 |
| 56 | 62 | 60 | 68 | 78 | 75 | 76 | 62 | 63 | 70 |
(2)求
 ,
,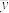 ,
,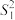 ,
,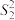 ;
;(3)依据以上计算结果进行分析,推广种植
 品种还是
品种还是 品种水稻更合适.
品种水稻更合适.
您最近一年使用:0次
2023-11-03更新
|
549次组卷
|
4卷引用:四川省成都市彭州市2023-2024学年高二上学期期中考试数学试题
四川省成都市彭州市2023-2024学年高二上学期期中考试数学试题四川省成都市蓉城名校联盟2023-2024学年高二上学期期中联考数学试题(已下线)第九章 统计(知识归纳+题型突破)(2) -单元速记·巧练(人教A版2019必修第二册)(已下线)模型5 利用统计量进行决策问题模型(第9章 统计)
2011·山西·一模
名校
解题方法
5 . 某中学的高二(1)班有男同学45名、女同学15名,老师按照分层抽样的方法组建了一个4人的课外兴趣小组.
(1)求某同学被抽到的概率及课外兴趣小组中男、女同学的人数;
(2)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出1名同学做实验,该同学做完后,再从小组内剩下的同学中选1名同学做实验,求选出的两名同学中恰有一名女同学的概率;
(3)实验结束后,第一次做实验的同学得到实验数据为68、70、71、72、74,第二次做实验的同学得到的实验数据为69、70、70、72、74,请问哪位同学的实验更稳定?并说明理由.
(1)求某同学被抽到的概率及课外兴趣小组中男、女同学的人数;
(2)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出1名同学做实验,该同学做完后,再从小组内剩下的同学中选1名同学做实验,求选出的两名同学中恰有一名女同学的概率;
(3)实验结束后,第一次做实验的同学得到实验数据为68、70、71、72、74,第二次做实验的同学得到的实验数据为69、70、70、72、74,请问哪位同学的实验更稳定?并说明理由.
您最近一年使用:0次
2023-02-06更新
|
701次组卷
|
21卷引用:2011-2012学年江西省横峰中学高二下学期期中考试文科数学试卷
(已下线)2011-2012学年江西省横峰中学高二下学期期中考试文科数学试卷福建省厦门市思明区厦门外国语学校2019-2020学年高二上学期期中数学试题新疆昌吉市教育共同体2019-2020学年高二上学期期中考试数学试题(已下线)2011届山西大学附中高三第二学期高三第一次模拟测试数学试卷(已下线)2011届黑龙江省大庆实验中学高三高考仿真模拟试题文数(已下线)2013届山东省淄博一中高三上学期期末模块考试文科数学试卷(已下线)2012-2013学年黑龙江省集贤县第一中学高二上学期期末理科数学试卷(已下线)2012-2013学年河南省唐河县第一高级中学高一下第一次月考数学卷(已下线)2015届山东师范大学附属中学高三第一次模拟考试文科数学试卷2016届湖南师大附中高三下学期高考模拟三文科数学试卷2015-2016学年湖北省仙桃市汉江高中高一下学期期末考试数学试卷辽宁省抚顺市省重点高中协作校2018-2019学年高一下学期期末数学试题甘肃省白银市会宁县第四中学2021届高三上学期第四次月考数学(文)试题沪教版(2020) 必修第三册 高效课堂 第十三章 13.7 复习与小结(已下线)第十章 概率 (练基础)(已下线)10.1.3 古典概型(精练)-【精讲精练】2022-2023学年高一数学下学期同步精讲精练(人教A版2019必修第二册)河北省唐山市第二中学2022-2023学年高一下学期期末数学试题山东省济宁市微山县第二中学2023-2024学年高二上学期第一次月考数学试题(已下线)10.1.3?古典概型——课后作业(巩固版)【巩固卷】第13章测评卷 单元测试A-沪教版(2020)必修第三册【基础卷】 第13章统计单元测试C-沪教版(2020)必修第三册
名校
6 . 为研究某地区2021届大学毕业生毕业三个月后的毕业去向,某调查公司从该地区2021届大学毕业生中随机选取了1000人作为样本进行调查,结果如下:
假设该地区2021届大学毕业生选择的毕业去向相互独立.
(1)若该地区一所高校2021届大学毕业生的人数为2500,试根据样本估计该校2021届大学毕业生选择“单位就业”的人数;
(2)从该地区2021届大学毕业生中随机选取3人,记随机变量 为这3人中选择“继续学习深造”的人数.以样本的频率估计概率,求
为这3人中选择“继续学习深造”的人数.以样本的频率估计概率,求 的分布列和数学期望
的分布列和数学期望 ;
;
(3)该公司在半年后对样本中的毕业生进行再调查,发现仅有选择“慢就业”的毕业生中的
 人选择了上表中其他的毕业去向,记此时表中五种毕业去向对应人数的方差为
人选择了上表中其他的毕业去向,记此时表中五种毕业去向对应人数的方差为 .当
.当 为何值时,
为何值时, 最小.(结论不要求证明)
最小.(结论不要求证明)
| 毕业去向 | 继续学习深造 | 单位就业 | 自主创业 | 自由职业 | 慢就业 |
| 人数 | 200 | 560 | 14 | 128 | 98 |
(1)若该地区一所高校2021届大学毕业生的人数为2500,试根据样本估计该校2021届大学毕业生选择“单位就业”的人数;
(2)从该地区2021届大学毕业生中随机选取3人,记随机变量
 为这3人中选择“继续学习深造”的人数.以样本的频率估计概率,求
为这3人中选择“继续学习深造”的人数.以样本的频率估计概率,求 的分布列和数学期望
的分布列和数学期望 ;
;(3)该公司在半年后对样本中的毕业生进行再调查,发现仅有选择“慢就业”的毕业生中的

 人选择了上表中其他的毕业去向,记此时表中五种毕业去向对应人数的方差为
人选择了上表中其他的毕业去向,记此时表中五种毕业去向对应人数的方差为 .当
.当 为何值时,
为何值时, 最小.(结论不要求证明)
最小.(结论不要求证明)
您最近一年使用:0次
2022-03-24更新
|
1426次组卷
|
8卷引用:北京市怀柔区第一中学2022-2023学年高二下学期期中考试数学试卷
解题方法
7 . 为了参加数学选拔赛,某高级中学对高二年级理科、文科两个数学兴趣小组的同学进行了赛前模拟测试,成绩(单位:分)记录如下:
理科:79,80,81,79,94,92,85,90
文科:94,80,90,81,73,84,90,80
(1)计算理科、文科两组同学成绩的平均数和方差,并从统计学的角度分析,哪组同学在此次模拟测试中发挥更好;
(2)若在成绩不低于90分的同学中随机抽出2人进行培训,求抽出的2人中至少有1名理科组同学的概率.
理科:79,80,81,79,94,92,85,90
文科:94,80,90,81,73,84,90,80
(1)计算理科、文科两组同学成绩的平均数和方差,并从统计学的角度分析,哪组同学在此次模拟测试中发挥更好;
(2)若在成绩不低于90分的同学中随机抽出2人进行培训,求抽出的2人中至少有1名理科组同学的概率.
您最近一年使用:0次
2021-07-12更新
|
260次组卷
|
3卷引用:广东省湛江市崇文高级中学2021-2022学年高二上学期期中测试数学试卷
名校
解题方法
8 . 小明同学两次测试成绩(满分100分)如下表所示:
(1)从小明同学第一次测试的科目中随机抽取1科,求该科成绩大于90分的概率;
(2)从小明同学第一次测试和第二次测试的科目中各随机抽取1科,记X为抽取的2科中成绩大于90分的科目数量,求X的分布列和数学期望 ;
;
(3)现有另一名同学两次测试成绩(满分100分)及相关统计信息如下表所示:
将每科两次测试成绩的均值作为该科的总评成绩,这6科总评成绩的方差为 .有一种观点认为:若
.有一种观点认为:若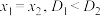 ,则
,则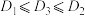 .你认为这种观点是否正确?(只写“正确”或“不正确”)
.你认为这种观点是否正确?(只写“正确”或“不正确”)
| 语文 | 数学 | 英语 | 物理 | 化学 | 生物 | |
| 第一次 | 87 | 92 | 91 | 92 | 85 | 93 |
| 第二次 | 82 | 94 | 95 | 88 | 94 | 87 |
(2)从小明同学第一次测试和第二次测试的科目中各随机抽取1科,记X为抽取的2科中成绩大于90分的科目数量,求X的分布列和数学期望
 ;
;(3)现有另一名同学两次测试成绩(满分100分)及相关统计信息如下表所示:
| 语文 | 数学 | 英语 | 物理 | 化学 | 生物 | 6科成绩均值 | 6科成绩方差 | |
| 第一次 |  |  |  |  |  | 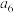 |  |  |
| 第二次 |  |  |  | 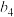 |  |  |  |  |
 .有一种观点认为:若
.有一种观点认为:若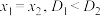 ,则
,则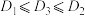 .你认为这种观点是否正确?(只写“正确”或“不正确”)
.你认为这种观点是否正确?(只写“正确”或“不正确”)
您最近一年使用:0次
2021-04-07更新
|
1169次组卷
|
8卷引用:北京市第二中学2022-2023学年高二下学期期中考试数学试题
名校
解题方法
9 . 随着经济全球化、信息化的发展,企业之间的竞争从资源的争夺转向人才的竞争,吸引、留住培养和用好人才成为人力资源管理的战略目标和紧迫任务,在此背景下,某信息网站在15个城市中对刚毕业的大学生的月平均收入薪资和月平均期望薪资做了调查,数据如下图所示.

(1)若某大学毕业生从这15座城市中随机选择一座城市就业,求该生选中月平均收入薪资高于8500元的城市的概率;
(2)现有2名大学毕业生在这15座城市中各随机选择一座城市就业,且2人的选择相互独立,记X为选中月平均收入薪资高于8500元的城市的人数,求X的分布列和数学期望E(X);
(3)记图中月平均收入薪资对应数据的方差为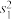 ,月平均期望薪资对应数据的方差为
,月平均期望薪资对应数据的方差为 ,判断
,判断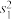 与
与 的大小(只需写出结论)
的大小(只需写出结论)

(1)若某大学毕业生从这15座城市中随机选择一座城市就业,求该生选中月平均收入薪资高于8500元的城市的概率;
(2)现有2名大学毕业生在这15座城市中各随机选择一座城市就业,且2人的选择相互独立,记X为选中月平均收入薪资高于8500元的城市的人数,求X的分布列和数学期望E(X);
(3)记图中月平均收入薪资对应数据的方差为
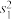 ,月平均期望薪资对应数据的方差为
,月平均期望薪资对应数据的方差为 ,判断
,判断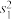 与
与 的大小(只需写出结论)
的大小(只需写出结论)
您最近一年使用:0次
2020-02-15更新
|
467次组卷
|
9卷引用:北京市育英学校2022-2023学年高二下学期期中练习数学试题
北京市育英学校2022-2023学年高二下学期期中练习数学试题2019年北京市丰台区高三(3月)模拟数学(理)(已下线)专题05 必拿分题目强化卷(第一篇)-备战2021年新高考数学分层强化训练(北京专版)(已下线)专题05 少丢分题目强化卷(第二篇)-备战2021年新高考数学分层强化训练(北京专版)福建省南平市浦城县2020-2021学年高二下学期第一次月考数学试题北京名校2023届高三二轮复习 专题六 概率与统计 第2讲 概率与统计北京市育英学校2021-2022学年高二普通班上学期期末练习数学试题北京市第五中学2024届高三上学期10月月考数学试题北京市第六十六中学2023-2024学年高二下学期6月月考质量检测数学试题

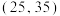
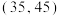
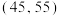
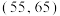
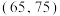
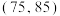
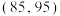
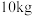 )
)

