名校
1 . 《中共中央国务院关于实现巩固拓展脱贫攻坚成果同乡村振兴有效衔接的意见》明确提出,支持脱贫地区乡村特色产业发展壮大,加快脱贫地区农产品和食品仓储保鲜、冷链物流设施建设,支持农产品流通企业、电商、批发市场与区域特色产业精准对接.当前,脱贫地区相关设施建设情况如何?怎样实现精准对接?未来如何进一步补齐发展短板?针对上述问题,假定有A、B、C三个解决方案,通过调查发现有 的受调查者赞成方案A,有
的受调查者赞成方案A,有 的受调查者赞成方案B,有
的受调查者赞成方案B,有 的受调查者赞成方案C,现有甲、乙、丙三人独立参加投票(以频率作为概率).
的受调查者赞成方案C,现有甲、乙、丙三人独立参加投票(以频率作为概率).
(1)求甲、乙两人投票方案不同的概率;
(2)若某人选择方案A或方案B,则对应方案可获得2票,选择方案C,则方案C获得1票,设 是甲、乙、丙三人投票后三个方案获得票数之和,求
是甲、乙、丙三人投票后三个方案获得票数之和,求 的分布列和数学期望.
的分布列和数学期望.
 的受调查者赞成方案A,有
的受调查者赞成方案A,有 的受调查者赞成方案B,有
的受调查者赞成方案B,有 的受调查者赞成方案C,现有甲、乙、丙三人独立参加投票(以频率作为概率).
的受调查者赞成方案C,现有甲、乙、丙三人独立参加投票(以频率作为概率).(1)求甲、乙两人投票方案不同的概率;
(2)若某人选择方案A或方案B,则对应方案可获得2票,选择方案C,则方案C获得1票,设
 是甲、乙、丙三人投票后三个方案获得票数之和,求
是甲、乙、丙三人投票后三个方案获得票数之和,求 的分布列和数学期望.
的分布列和数学期望.
您最近一年使用:0次
2022-03-14更新
|
1825次组卷
|
4卷引用:黑龙江省哈尔滨市第七十三中学校2022-2023学年高三上学期第一次月考数学试题
黑龙江省哈尔滨市第七十三中学校2022-2023学年高三上学期第一次月考数学试题2022年普通高等学校招生全国统一考试数学模拟测试(新高考)(已下线)临考押题卷05-2022年高考数学临考押题卷(新高考卷)辽宁省沈阳市第二十中学2023-2024学年高三上学期三模考试数学试题
名校
解题方法
2 . 核酸检测是诊断新冠肺炎的重要依据,首先取病人的唾液或咽拭子的样本,再提取唾液或咽拭子样本里的遗传物质,如果有病毒,样本检测会呈现阳性,否则为阴性.根据统计发现,疑似病例核酸检测呈阳性的概率为 ,现有4例疑似病例,分别对其取样、检测,多个样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验,混合样本中只要有病毒,则混合样本化验结果就会呈阳性,若混合样本呈阳性,则将该组中各个样本再逐个化验;若混合样本呈阴性,则该组各个样本均为阴性.现有以下三种方案:方案一:逐个化验;方案二:四个样本混在一起化验;方案三:平均分成两组化验.在新冠肺炎爆发初期,由于检查能力不足,化检次数的期望值越小,则方案越“优”.
,现有4例疑似病例,分别对其取样、检测,多个样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验,混合样本中只要有病毒,则混合样本化验结果就会呈阳性,若混合样本呈阳性,则将该组中各个样本再逐个化验;若混合样本呈阴性,则该组各个样本均为阴性.现有以下三种方案:方案一:逐个化验;方案二:四个样本混在一起化验;方案三:平均分成两组化验.在新冠肺炎爆发初期,由于检查能力不足,化检次数的期望值越小,则方案越“优”.
(1)若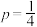 ,求2个疑似病例样本混合化验结果为阳性的概率;
,求2个疑似病例样本混合化验结果为阳性的概率;
(2)若 ,现将该4例疑似病例样本进行化验,请问:方案一、二、三中哪个最“优”?
,现将该4例疑似病例样本进行化验,请问:方案一、二、三中哪个最“优”?
(3)若对4例疑似病例样本进行化验,且“方案一”比“方案二”更“优”,求 的取值范围.
的取值范围.
 ,现有4例疑似病例,分别对其取样、检测,多个样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验,混合样本中只要有病毒,则混合样本化验结果就会呈阳性,若混合样本呈阳性,则将该组中各个样本再逐个化验;若混合样本呈阴性,则该组各个样本均为阴性.现有以下三种方案:方案一:逐个化验;方案二:四个样本混在一起化验;方案三:平均分成两组化验.在新冠肺炎爆发初期,由于检查能力不足,化检次数的期望值越小,则方案越“优”.
,现有4例疑似病例,分别对其取样、检测,多个样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验,混合样本中只要有病毒,则混合样本化验结果就会呈阳性,若混合样本呈阳性,则将该组中各个样本再逐个化验;若混合样本呈阴性,则该组各个样本均为阴性.现有以下三种方案:方案一:逐个化验;方案二:四个样本混在一起化验;方案三:平均分成两组化验.在新冠肺炎爆发初期,由于检查能力不足,化检次数的期望值越小,则方案越“优”.(1)若
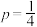 ,求2个疑似病例样本混合化验结果为阳性的概率;
,求2个疑似病例样本混合化验结果为阳性的概率;(2)若
 ,现将该4例疑似病例样本进行化验,请问:方案一、二、三中哪个最“优”?
,现将该4例疑似病例样本进行化验,请问:方案一、二、三中哪个最“优”?(3)若对4例疑似病例样本进行化验,且“方案一”比“方案二”更“优”,求
 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
3 . 某大型公司为了切实保障员工的健康安全,贯彻好卫生防疫工作的相关要求,决定在全公司范围内举行一次乙肝普查.为此需要抽验669人的血样进行化验,由于人数较多,检疫部门制定了下列两种可供选择的方案.
方案一:将每个人的血分别化验,这时需要验669次.
方案二:按 个人一组进行随机分组,把从每组
个人一组进行随机分组,把从每组 个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这
个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这 个人的血就只需检验一次(这时认为每个人的血化验
个人的血就只需检验一次(这时认为每个人的血化验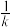 次);否则,若呈阳性,则需对这
次);否则,若呈阳性,则需对这 个人的血样再分别进行一次化验,这时该组
个人的血样再分别进行一次化验,这时该组 个人的血总共需要化验
个人的血总共需要化验 次.
次.
假设此次普查中每个人的血样化验呈阳性的概率为 ,且这些人之间的试验反应相互独立.
,且这些人之间的试验反应相互独立.
(1)设方案二中,某组 个人中每个人的血化验次数为
个人中每个人的血化验次数为 ,求
,求 的分布列.
的分布列.
(2)设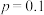 ,试比较方案二中,
,试比较方案二中, 分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案一,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数)
分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案一,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数)
方案一:将每个人的血分别化验,这时需要验669次.
方案二:按
 个人一组进行随机分组,把从每组
个人一组进行随机分组,把从每组 个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这
个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这 个人的血就只需检验一次(这时认为每个人的血化验
个人的血就只需检验一次(这时认为每个人的血化验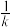 次);否则,若呈阳性,则需对这
次);否则,若呈阳性,则需对这 个人的血样再分别进行一次化验,这时该组
个人的血样再分别进行一次化验,这时该组 个人的血总共需要化验
个人的血总共需要化验 次.
次.假设此次普查中每个人的血样化验呈阳性的概率为
 ,且这些人之间的试验反应相互独立.
,且这些人之间的试验反应相互独立.(1)设方案二中,某组
 个人中每个人的血化验次数为
个人中每个人的血化验次数为 ,求
,求 的分布列.
的分布列.(2)设
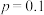 ,试比较方案二中,
,试比较方案二中, 分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案一,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数)
分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案一,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数)
您最近一年使用:0次
2020-05-09更新
|
902次组卷
|
8卷引用:2020届黑龙江省大庆实验中学高三5月第一次模拟数学(理)试题
2020届黑龙江省大庆实验中学高三5月第一次模拟数学(理)试题2020届河北省保定市高三上学期期末数学(理)试题2020届河北省廊坊市上学期高三期末数学理科试题2020届河南省六市(南阳市、驻马店市、信阳市、漯河市、周口市、三门峡市)高三第一次模拟调研理数试题河北省2019-2020学年高三下学期名优校联考数学(理)试题(已下线)专题07 比较两类方法或者策略的分析问题(第四篇)-备战2020年高考数学大题精做之解答题题型全覆盖(已下线)专题03 概率统计(理)第三篇-备战2020高考数学黄金30题系列之压轴题(新课标版)(已下线)江苏省苏锡常镇四市2023届高三下学期3月教学情况调研(一)数学试题变式题17-22
名校
4 . 新冠病毒是一种通过飞沫和接触传播的变异病毒,为筛查该病毒,有一种检验方式是检验血液样本相关指标是否为阳性,对于 份血液样本,有以下两种检验方式:一是逐份检验,则需检验
份血液样本,有以下两种检验方式:一是逐份检验,则需检验 次.二是混合检验,将其中
次.二是混合检验,将其中 份血液样本分别取样混合在一起,若检验结果为阴性,那么这
份血液样本分别取样混合在一起,若检验结果为阴性,那么这 份血液全为阴性,因而检验一次就够了;如果检验结果为阳性,为了明确这
份血液全为阴性,因而检验一次就够了;如果检验结果为阳性,为了明确这 份血液究竟哪些为阳性,就需要对它们再逐份检验,此时
份血液究竟哪些为阳性,就需要对它们再逐份检验,此时 份血液检验的次数总共为
份血液检验的次数总共为 次.某定点医院现取得4份血液样本,考虑以下三种检验方案:方案一,逐个检验;方案二,平均分成两组检验;方案三,四个样本混在一起检验.假设在接受检验的血液样本中,每份样本检验结果是阳性还是阴性都是相互独立的,且每份样本是阴性的概率为
次.某定点医院现取得4份血液样本,考虑以下三种检验方案:方案一,逐个检验;方案二,平均分成两组检验;方案三,四个样本混在一起检验.假设在接受检验的血液样本中,每份样本检验结果是阳性还是阴性都是相互独立的,且每份样本是阴性的概率为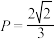 .
.
(Ⅰ)求把2份血液样本混合检验结果为阳性的概率;
(Ⅱ)若检验次数的期望值越小,则方案越“优”.方案一、二、三中哪个最“优”?请说明理由.
 份血液样本,有以下两种检验方式:一是逐份检验,则需检验
份血液样本,有以下两种检验方式:一是逐份检验,则需检验 次.二是混合检验,将其中
次.二是混合检验,将其中 份血液样本分别取样混合在一起,若检验结果为阴性,那么这
份血液样本分别取样混合在一起,若检验结果为阴性,那么这 份血液全为阴性,因而检验一次就够了;如果检验结果为阳性,为了明确这
份血液全为阴性,因而检验一次就够了;如果检验结果为阳性,为了明确这 份血液究竟哪些为阳性,就需要对它们再逐份检验,此时
份血液究竟哪些为阳性,就需要对它们再逐份检验,此时 份血液检验的次数总共为
份血液检验的次数总共为 次.某定点医院现取得4份血液样本,考虑以下三种检验方案:方案一,逐个检验;方案二,平均分成两组检验;方案三,四个样本混在一起检验.假设在接受检验的血液样本中,每份样本检验结果是阳性还是阴性都是相互独立的,且每份样本是阴性的概率为
次.某定点医院现取得4份血液样本,考虑以下三种检验方案:方案一,逐个检验;方案二,平均分成两组检验;方案三,四个样本混在一起检验.假设在接受检验的血液样本中,每份样本检验结果是阳性还是阴性都是相互独立的,且每份样本是阴性的概率为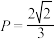 .
.(Ⅰ)求把2份血液样本混合检验结果为阳性的概率;
(Ⅱ)若检验次数的期望值越小,则方案越“优”.方案一、二、三中哪个最“优”?请说明理由.
您最近一年使用:0次
2020-05-05更新
|
1288次组卷
|
15卷引用:黑龙江省哈尔滨市第三十二中学2020-2021学年高三上学期期末考试理科数学试题
黑龙江省哈尔滨市第三十二中学2020-2021学年高三上学期期末考试理科数学试题黑龙江省哈尔滨市哈尔滨德强学校2022-2023学年高二下学期3月月考数学试题山西省太原市2019-2020学年高三下学期模拟(一)数学(理)试题四川省双流中学2019-2020学年高三5月月考数学(理)试题甘肃省静宁县第一中学2020届高三第七次模拟考试数学(理)试题重庆市渝北区、合川区、江北区等七区2019-2020学年高二下学期期末联考数学试题山西省朔州市怀仁县怀仁一中云东校区2019-2020学年高二下学期期末数学(理)试题2020届山西省太原市高三一模数学(理)试题(已下线)专题05 概率——2020年高考数学母题题源解密(山东、海南专版)陕西省西安市长安区第一中学2020-2021学年高三上学期第一次教学质量检测数学(理)试题广西桂林市第五中学2021届高三第一学期期末复习数学试题(一)山西省长治市第二中学2021届高三上学期第六次练考数学(理)试题四川省内江市第六中学2020-2021学年高三下学期第五次月考数学(理科)试题江苏省南京市大厂高级中学2020-2021学年高三上学期1月阶段学情调研数学试题宁夏石嘴山市2022届高三适应性测试数学(理)试题
解题方法
5 . 五一期间,某商场决定从 种服装、
种服装、 种家电、
种家电、 种日用品中,选出
种日用品中,选出 种商品进行促销活动.
种商品进行促销活动.
(1)试求选出 种商品中至少有一种是家电的概率;
种商品中至少有一种是家电的概率;
(2)商场对选出的某商品采用抽奖方式进行促销,即在该商品现价的基础上将价格提高 元,规定购买该商品的顾客有
元,规定购买该商品的顾客有 次抽奖的机会: 若中一次奖,则获得数额为
次抽奖的机会: 若中一次奖,则获得数额为 元的奖金;若中两次奖,则获得数额为
元的奖金;若中两次奖,则获得数额为 元的奖金;若中三次奖,则共获得数额为
元的奖金;若中三次奖,则共获得数额为  元的奖金. 假设顾客每次抽奖中奖的概率都是
元的奖金. 假设顾客每次抽奖中奖的概率都是 ,请问:商场将奖金数额
,请问:商场将奖金数额 最高定为多少元,才能使促销方案对商场有利?
最高定为多少元,才能使促销方案对商场有利?
 种服装、
种服装、 种家电、
种家电、 种日用品中,选出
种日用品中,选出 种商品进行促销活动.
种商品进行促销活动.(1)试求选出
 种商品中至少有一种是家电的概率;
种商品中至少有一种是家电的概率;(2)商场对选出的某商品采用抽奖方式进行促销,即在该商品现价的基础上将价格提高
 元,规定购买该商品的顾客有
元,规定购买该商品的顾客有 次抽奖的机会: 若中一次奖,则获得数额为
次抽奖的机会: 若中一次奖,则获得数额为 元的奖金;若中两次奖,则获得数额为
元的奖金;若中两次奖,则获得数额为 元的奖金;若中三次奖,则共获得数额为
元的奖金;若中三次奖,则共获得数额为  元的奖金. 假设顾客每次抽奖中奖的概率都是
元的奖金. 假设顾客每次抽奖中奖的概率都是 ,请问:商场将奖金数额
,请问:商场将奖金数额 最高定为多少元,才能使促销方案对商场有利?
最高定为多少元,才能使促销方案对商场有利?
您最近一年使用:0次
2017-04-27更新
|
290次组卷
|
2卷引用:2017届黑龙江省大庆市高三第三次教学质量检测(三模)数学(理)试卷



