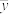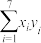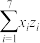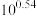2023·湖南·模拟预测
解题方法
1 . 华为云服务是华为公司在ICT领域通过30多年的技术攻坚和经验积累,将产品解决方案开放给用户,为用户提供集个人数据同步、云相册、手机找回等多种基础云功能,旨在为消费者提供一站式易用、快捷、智能、安全的个人数据管理服务.华为云服务采用按需使用、按需付费的一站式IT计算资源租用服务.据调查,在某一地区自2016年至2022年以来,7年的使用用户数如下表所示:(x表示年度,2016年度记为1,2017年度记为2,…,依次类推,2022年度记为7;y表示该年度使用的用户数,单位:千户).
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
y | 7 | 9 | 21 | 36 | 66 | 100 | 198 |

根据以上数据,绘制了如图所示的散点图.
(1)根据散点图判断,在这7年内,
 与
与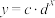 (c,d均为大于零的常数)哪一个适宜作为该地区华为云用户数
(c,d均为大于零的常数)哪一个适宜作为该地区华为云用户数 (千户)关于年度
(千户)关于年度 的回归方程类型?(给出判断即可,不必说明理由);并根据表中数据,求
的回归方程类型?(给出判断即可,不必说明理由);并根据表中数据,求 关于
关于 的经验回归方程,估计2023年度用户数(保留到千户位);
的经验回归方程,估计2023年度用户数(保留到千户位);(2)该地区按用户使用华为云服务的时间,从高到低评为三个等第的星级,其中连续使用华为云5年以上的用户评为“五星用户”,三年以上五年以下的用户评为“三星用户”,其它用户评为“星级用户”,每位用户年服务费按星级从高到低依次为50元、70元、90元.为了拓展用户数量,该地区今年推出一项用户星级升级的抽奖活动,每位用户可抽奖两次,每次抽奖有
 的概率升两级,有
的概率升两级,有 的概率升一级,还有
的概率升一级,还有 的概率不升级,最高升为“五星用户”.现某家庭有2位华为云用户,其中甲是“三星用户”,乙是“星级用户”,求今年该家庭支付华为云服务费的分布列与数学期望.
的概率不升级,最高升为“五星用户”.现某家庭有2位华为云用户,其中甲是“三星用户”,乙是“星级用户”,求今年该家庭支付华为云服务费的分布列与数学期望.参考数据:
|
|
|
|
|
62.43 | 1.54 | 2548 | 50.12 | 3.47 |
其中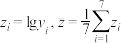 .
.
参考公式:经验回归直线方程 中斜率与截距的最小二乘法估计公式分别为
中斜率与截距的最小二乘法估计公式分别为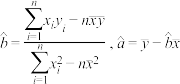 .
.
您最近一年使用:0次
2 . 在概率论发展的过程中,通过构造试验推翻或验证某些结论是统计学家们常用的方法,若事件A,B,C满足 ,
,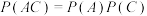 ,
,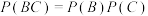 同时成立,则称事件A,B,C两两独立,现有一个正六面体,六个面分别标有1到6的六个数,随机抛掷该六面体一次,观察与地面接触的面上的数字,得到样本空间
同时成立,则称事件A,B,C两两独立,现有一个正六面体,六个面分别标有1到6的六个数,随机抛掷该六面体一次,观察与地面接触的面上的数字,得到样本空间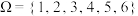 ,若
,若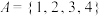 ,
,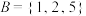 ,则可以构造C=
,则可以构造C=______ (填一个满足条件的即可),使得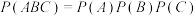 成立时,但不满足事件A,B,C两两独立
成立时,但不满足事件A,B,C两两独立
 ,
,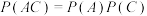 ,
,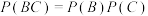 同时成立,则称事件A,B,C两两独立,现有一个正六面体,六个面分别标有1到6的六个数,随机抛掷该六面体一次,观察与地面接触的面上的数字,得到样本空间
同时成立,则称事件A,B,C两两独立,现有一个正六面体,六个面分别标有1到6的六个数,随机抛掷该六面体一次,观察与地面接触的面上的数字,得到样本空间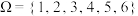 ,若
,若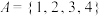 ,
,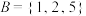 ,则可以构造C=
,则可以构造C=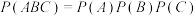 成立时,但不满足事件A,B,C两两独立
成立时,但不满足事件A,B,C两两独立
您最近一年使用:0次
2022-11-16更新
|
782次组卷
|
4卷引用:高考新题型-概率
(已下线)高考新题型-概率(已下线)模块八 专题5 以概率与统计为背景的压轴小题云南省云南师范大学附属中学2023届高考适应性月考卷(五)数学试题广东省广州市中山大学附属中学2023届高三上学期期中数学试题
2022·福建三明·模拟预测
名校
3 . 当前,新一轮科技革命和产业变革蓬勃兴起,以区块链为代表的新一代信息技术迅猛发展,现收集某地近5年区块链企业总数量相关数据,如下表
(1)根据表中数据判断, 与
与 (其中
(其中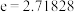 …为自然对数的底数),哪一个回归方程类型适宜预测未来几年我国区块链企业总数量?(给出结果即可,不必说明理由),并根据你的判断结果求y关于x的回归方程;
…为自然对数的底数),哪一个回归方程类型适宜预测未来几年我国区块链企业总数量?(给出结果即可,不必说明理由),并根据你的判断结果求y关于x的回归方程;
(2)为了促进公司间的合作与发展,区块链联合总部决定进行一次信息化技术比赛,邀请甲、乙、丙三家区块链公司参赛.比赛规则如下:①每场比赛有两个公司参加,并决出胜负;②每场比赛获胜的公司与未参加此场比赛的公司进行下一场的比赛;③在比赛中,若有一个公司首先获胜两场,则本次比赛结束,该公司获得此次信息化比赛的“优胜公司”.已知在每场比赛中,甲胜乙的概率为 ,甲胜丙的概率为
,甲胜丙的概率为 ,乙胜丙的概率为
,乙胜丙的概率为 ,若首场由甲乙比赛,求甲公司获得“优胜公司”的概率.
,若首场由甲乙比赛,求甲公司获得“优胜公司”的概率.
参考数据: ,
, ,
, ,
,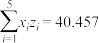 (其中
(其中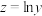 ).
).
附:样本 的最小二乘法估计公式为
的最小二乘法估计公式为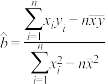 ,
,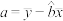 .
.
| 年份 | 2017 | 2018 | 2019 | 2020 | 2021 |
| 编号x | 1 | 2 | 3 | 4 | 5 |
| 企业总数量y(单位:千个) | 2.156 | 3.727 | 8.305 | 24.279 | 36.224 |
 与
与 (其中
(其中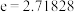 …为自然对数的底数),哪一个回归方程类型适宜预测未来几年我国区块链企业总数量?(给出结果即可,不必说明理由),并根据你的判断结果求y关于x的回归方程;
…为自然对数的底数),哪一个回归方程类型适宜预测未来几年我国区块链企业总数量?(给出结果即可,不必说明理由),并根据你的判断结果求y关于x的回归方程;(2)为了促进公司间的合作与发展,区块链联合总部决定进行一次信息化技术比赛,邀请甲、乙、丙三家区块链公司参赛.比赛规则如下:①每场比赛有两个公司参加,并决出胜负;②每场比赛获胜的公司与未参加此场比赛的公司进行下一场的比赛;③在比赛中,若有一个公司首先获胜两场,则本次比赛结束,该公司获得此次信息化比赛的“优胜公司”.已知在每场比赛中,甲胜乙的概率为
 ,甲胜丙的概率为
,甲胜丙的概率为 ,乙胜丙的概率为
,乙胜丙的概率为 ,若首场由甲乙比赛,求甲公司获得“优胜公司”的概率.
,若首场由甲乙比赛,求甲公司获得“优胜公司”的概率.参考数据:
 ,
, ,
, ,
,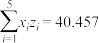 (其中
(其中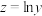 ).
).附:样本
 的最小二乘法估计公式为
的最小二乘法估计公式为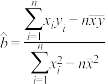 ,
,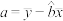 .
.
您最近一年使用:0次
2022-06-14更新
|
983次组卷
|
5卷引用:8.5 统计案例(精讲)
2024·全国·模拟预测
4 . 某高校航天研究小组在某课题结束后对参与的学生进行结业测评,每位学生分两轮进行:第一轮是5个基础项目的逐项测评,若连续通过2个即可停止第一轮测评,进入第二轮测评;第二轮是从5个技能展示项目中随机抽取3个进行测评,若全部通过则通过结业测评,若有项目不通过,则需要重新进行第二轮测评,直至通过为止.已知学生甲通过每个基础项目的概率都是 ,且各个基础项目的测评结果互不影响;他对5个技能展示项目中的4个有把握一次性通过,唯有一个在第一次通过的概率为
,且各个基础项目的测评结果互不影响;他对5个技能展示项目中的4个有把握一次性通过,唯有一个在第一次通过的概率为 ,第二次通过的概率为
,第二次通过的概率为 ,第三次通过的概率为
,第三次通过的概率为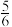 ,第四次才有把握一定通过.
,第四次才有把握一定通过.
(1)求甲至多进行4个基础项目就能通过第一轮测评的概率;
(2)记 为甲参加第二轮测评的次数,求
为甲参加第二轮测评的次数,求 的分布列及数学期望.
的分布列及数学期望.
 ,且各个基础项目的测评结果互不影响;他对5个技能展示项目中的4个有把握一次性通过,唯有一个在第一次通过的概率为
,且各个基础项目的测评结果互不影响;他对5个技能展示项目中的4个有把握一次性通过,唯有一个在第一次通过的概率为 ,第二次通过的概率为
,第二次通过的概率为 ,第三次通过的概率为
,第三次通过的概率为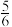 ,第四次才有把握一定通过.
,第四次才有把握一定通过.(1)求甲至多进行4个基础项目就能通过第一轮测评的概率;
(2)记
 为甲参加第二轮测评的次数,求
为甲参加第二轮测评的次数,求 的分布列及数学期望.
的分布列及数学期望.
您最近一年使用:0次
21-22高三下·青海玉树·阶段练习
5 . 某紫砂壶加工工坊在加工一批紫砂壶时,在出窑过程中有的会因为气温骤冷、泥料膨胀率不均等原因导致紫砂壶出现一定的瑕疵而形成次品,有的直接损毁.通常情况下,一把紫砂壶的成品率为 ,损毁率为
,损毁率为 .对于烧窑过程中出现的次品,会通过再次整形调整后入窑复烧,二次出窑,其在二次出窑时不出现次品,成品率为
.对于烧窑过程中出现的次品,会通过再次整形调整后入窑复烧,二次出窑,其在二次出窑时不出现次品,成品率为 .已知一把紫砂壶加工的泥料成本为500元/把,每把壶的平均烧窑成本为50元/次,复烧前的整形工费为100元/次,成品即可对外销售,售价均为1500元.
.已知一把紫砂壶加工的泥料成本为500元/把,每把壶的平均烧窑成本为50元/次,复烧前的整形工费为100元/次,成品即可对外销售,售价均为1500元.
(1)求一把紫砂壶能够对外销售的概率;
(2)某客户在一批紫砂壶入窑前随机对一把紫砂壶坯料进行了标记,求被标记的紫砂壶的最终获利X的数学期望.
 ,损毁率为
,损毁率为 .对于烧窑过程中出现的次品,会通过再次整形调整后入窑复烧,二次出窑,其在二次出窑时不出现次品,成品率为
.对于烧窑过程中出现的次品,会通过再次整形调整后入窑复烧,二次出窑,其在二次出窑时不出现次品,成品率为 .已知一把紫砂壶加工的泥料成本为500元/把,每把壶的平均烧窑成本为50元/次,复烧前的整形工费为100元/次,成品即可对外销售,售价均为1500元.
.已知一把紫砂壶加工的泥料成本为500元/把,每把壶的平均烧窑成本为50元/次,复烧前的整形工费为100元/次,成品即可对外销售,售价均为1500元.(1)求一把紫砂壶能够对外销售的概率;
(2)某客户在一批紫砂壶入窑前随机对一把紫砂壶坯料进行了标记,求被标记的紫砂壶的最终获利X的数学期望.
您最近一年使用:0次
2022-06-10更新
|
731次组卷
|
5卷引用:2022年全国高考甲卷数学(理)试题变式题9-12题
(已下线)2022年全国高考甲卷数学(理)试题变式题9-12题(已下线)2022年全国高考甲卷数学(理)试题变式题9-12题(已下线)2022年全国高考甲卷数学(理)试题变式题17-20题青海省玉树州州直高中2021-2022学年高三下学期第四次大联考数学(理科)试题2022届全国新高考Ⅱ卷仿真模拟数学试卷(五)
20-21高三下·全国·阶段练习
解题方法
6 . 滑雪是冰雪运动中深受人们喜爱的运动项目,为了了解某市 ,
, 两个专业滑雪队的技术水平,从这两个队各随机抽取了
两个专业滑雪队的技术水平,从这两个队各随机抽取了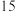 名队员进行比赛(百分制),其得分如图所示茎叶图.
名队员进行比赛(百分制),其得分如图所示茎叶图.
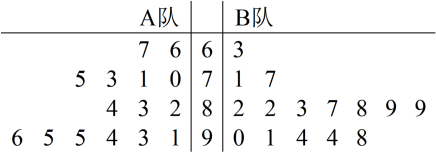
(1)通过茎叶图比较 ,
, 两队比赛得分的平均值
两队比赛得分的平均值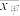 ,
, 的大小及分散程度(不要求计算,给出结论即可);
的大小及分散程度(不要求计算,给出结论即可);
(2)规定得分在 ,认定该队员滑雪技术为
,认定该队员滑雪技术为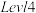 级,在
级,在 认定该队员滑雪技术为
认定该队员滑雪技术为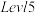 级,在
级,在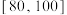 认定该队员滑雪技术为
认定该队员滑雪技术为 级.
级.
①现从得分在 的样本队员中,按照
的样本队员中,按照 队与
队与 队两大类,用分层抽样的方法随机抽取
队两大类,用分层抽样的方法随机抽取 人进行问卷调查,求这
人进行问卷调查,求这 名队员中恰含
名队员中恰含 、
、 两队所有滑雪技术为
两队所有滑雪技术为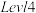 级的队员的概率;
级的队员的概率;
②从样本中任取 名队员,在认定这两名队员滑雪技术为
名队员,在认定这两名队员滑雪技术为 级情况下,求这
级情况下,求这 名队员来自同一滑雪队的概率.
名队员来自同一滑雪队的概率.
 ,
, 两个专业滑雪队的技术水平,从这两个队各随机抽取了
两个专业滑雪队的技术水平,从这两个队各随机抽取了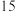 名队员进行比赛(百分制),其得分如图所示茎叶图.
名队员进行比赛(百分制),其得分如图所示茎叶图.
(1)通过茎叶图比较
 ,
, 两队比赛得分的平均值
两队比赛得分的平均值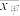 ,
, 的大小及分散程度(不要求计算,给出结论即可);
的大小及分散程度(不要求计算,给出结论即可);(2)规定得分在
 ,认定该队员滑雪技术为
,认定该队员滑雪技术为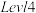 级,在
级,在 认定该队员滑雪技术为
认定该队员滑雪技术为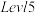 级,在
级,在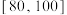 认定该队员滑雪技术为
认定该队员滑雪技术为 级.
级.①现从得分在
 的样本队员中,按照
的样本队员中,按照 队与
队与 队两大类,用分层抽样的方法随机抽取
队两大类,用分层抽样的方法随机抽取 人进行问卷调查,求这
人进行问卷调查,求这 名队员中恰含
名队员中恰含 、
、 两队所有滑雪技术为
两队所有滑雪技术为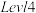 级的队员的概率;
级的队员的概率;②从样本中任取
 名队员,在认定这两名队员滑雪技术为
名队员,在认定这两名队员滑雪技术为 级情况下,求这
级情况下,求这 名队员来自同一滑雪队的概率.
名队员来自同一滑雪队的概率.
您最近一年使用:0次
2023·全国·模拟预测
解题方法
7 . 为了引导人民强健体魄,某市组织了一系列活动,其中乒乓球比赛的冠军由A,B两队争夺,已知A,B两队之间的比赛采用5局3胜制,且本次比赛共设有3000元奖金,奖金分配规则如下:①若比赛进行3局即可决定胜负,则赢方获得全部奖金,输方没有奖金;②若比赛进行4局即可决定胜负,则赢方获得90%的奖金,输方获得10%的奖金;③若比赛打满5局才决定胜负,则赢方获得80%的奖金,输方获得20%的奖金.已知每局比赛A队,B队赢的概率分别为 ,
, ,且每局比赛的结果相互独立.
,且每局比赛的结果相互独立.
(1)若比赛进行4局即可决定胜负,则A队赢得比赛的概率为多少?
(2)求A队获得奖金金额X的分布列及数学期望.
 ,
, ,且每局比赛的结果相互独立.
,且每局比赛的结果相互独立.(1)若比赛进行4局即可决定胜负,则A队赢得比赛的概率为多少?
(2)求A队获得奖金金额X的分布列及数学期望.
您最近一年使用:0次
2024高三下·全国·专题练习
8 . 某医学研究员随机抽取了5名甲流疑似病例,其中仅有一人感染甲流,通过化验血液来确认感染甲流的人,化验结果只有阴性和阳性两种,若结果呈阳性,则为甲流感染者,现有两个检测方案.
方案一:先从5人中随机抽取2人,将其血液混合进行1次检测,若结果呈阳性,则选择这2人中的1人检测即可;若结果呈阴性,则再对另外3人进行检测,每次只检测一个人,找到甲流感染者则停止检测.
方案二:将5人逐个检测,找到甲流感染者则停止检测.
(1)分别求出方案一、方案二所需检测次数的分布列与数学期望;
(2)若两种检测方案互不影响,求两种方案检测次数相等的概率;
(3)若检测费用为400元/次,请分别计算利用方案一、方案二检测的总费用的期望值,并以此作为决策依据,判断选择哪个方案更好.
方案一:先从5人中随机抽取2人,将其血液混合进行1次检测,若结果呈阳性,则选择这2人中的1人检测即可;若结果呈阴性,则再对另外3人进行检测,每次只检测一个人,找到甲流感染者则停止检测.
方案二:将5人逐个检测,找到甲流感染者则停止检测.
(1)分别求出方案一、方案二所需检测次数的分布列与数学期望;
(2)若两种检测方案互不影响,求两种方案检测次数相等的概率;
(3)若检测费用为400元/次,请分别计算利用方案一、方案二检测的总费用的期望值,并以此作为决策依据,判断选择哪个方案更好.
您最近一年使用:0次
2023·全国·模拟预测
名校
9 . 调查问卷中常常涉及到个人隐私或本人不愿正面回答的问题,被访人可能拒绝回答,即使回答,也不能期望答案是真实的.某小区要调查业主对物业工作是否满意的真实情况,现利用“随机化选答抽样”方法制作了具体调查方案,其操作流程如下:在一个箱子里放3个红球和2个白球,被调查者在摸到球后记住颜色并立即将球放回,如果抽到的是红球,则回答“你的性别是否为男性?”如果抽到的是白球,则回答“你对物业工作现状是否满意?”两个问题均用“是”或“否”回答.
(1)共收取调查问卷100份,其中答案为“是”的问卷为60份,求一个业主对物业工作表示满意的概率,已知该小区共有业主500人,估计该小区业主对物业工作满意的人数;
(2)现为了提高对物业工作满意的业主比例,对小区业主进行随机访谈,请表示不满意的业主在访谈中提出两个有待改进的问题.
(i)若物业对每一个待改进的问题均提出一个相应的解决方案,该方案需要由5名业主委员会代表投票决定是否可行.每位代表投赞同票的概率均为 ,方案需至少3人投赞成票,方能予以通过,并最终解决该问题,求某个问题能够被解决的概率
,方案需至少3人投赞成票,方能予以通过,并最终解决该问题,求某个问题能够被解决的概率 ;
;
(ii)假设业主所提问题各不相同,每一个问题能够被解决的概率都为 ,并且都相互独立.物业每解决一个问题,业主满意的比例将提高一个百分点.为了让业主满意的比例提高到80%,试估计至少要访谈多少位业主?
,并且都相互独立.物业每解决一个问题,业主满意的比例将提高一个百分点.为了让业主满意的比例提高到80%,试估计至少要访谈多少位业主?
(1)共收取调查问卷100份,其中答案为“是”的问卷为60份,求一个业主对物业工作表示满意的概率,已知该小区共有业主500人,估计该小区业主对物业工作满意的人数;
(2)现为了提高对物业工作满意的业主比例,对小区业主进行随机访谈,请表示不满意的业主在访谈中提出两个有待改进的问题.
(i)若物业对每一个待改进的问题均提出一个相应的解决方案,该方案需要由5名业主委员会代表投票决定是否可行.每位代表投赞同票的概率均为
 ,方案需至少3人投赞成票,方能予以通过,并最终解决该问题,求某个问题能够被解决的概率
,方案需至少3人投赞成票,方能予以通过,并最终解决该问题,求某个问题能够被解决的概率 ;
;(ii)假设业主所提问题各不相同,每一个问题能够被解决的概率都为
 ,并且都相互独立.物业每解决一个问题,业主满意的比例将提高一个百分点.为了让业主满意的比例提高到80%,试估计至少要访谈多少位业主?
,并且都相互独立.物业每解决一个问题,业主满意的比例将提高一个百分点.为了让业主满意的比例提高到80%,试估计至少要访谈多少位业主?
您最近一年使用:0次
2023·全国·模拟预测
解题方法
10 . 在购物节活动期间,某购物平台上的一个电商在其官方旗舰店举行有奖购物活动,奖励规则如下:购物预付款(单位:元)为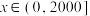 ,购物时可随机获得1个红包,其中红包面值为
,购物时可随机获得1个红包,其中红包面值为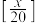 (
( 为不超过
为不超过 的最大整数)元的概率为
的最大整数)元的概率为 ,红包面值为
,红包面值为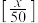 元的概率为
元的概率为 .若消费者预付款不低于500元,同时关注该店铺可以再获得一个红包,其中红包面值为20元的概率为
.若消费者预付款不低于500元,同时关注该店铺可以再获得一个红包,其中红包面值为20元的概率为 ,红包面值为60元的概率为
,红包面值为60元的概率为 .
.
(1)已知小李在该店铺购买了预付款为2000元的商品,且关注了该店铺,求小李实际付款不超过1900元的概率.
(2)若甲、乙两位消费者在该店铺都购买了预付款为2000元的商品,且都关注了该店铺,记甲、乙实际付款分别为 ,
, 元.令
元.令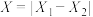 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
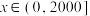 ,购物时可随机获得1个红包,其中红包面值为
,购物时可随机获得1个红包,其中红包面值为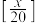 (
( 为不超过
为不超过 的最大整数)元的概率为
的最大整数)元的概率为 ,红包面值为
,红包面值为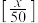 元的概率为
元的概率为 .若消费者预付款不低于500元,同时关注该店铺可以再获得一个红包,其中红包面值为20元的概率为
.若消费者预付款不低于500元,同时关注该店铺可以再获得一个红包,其中红包面值为20元的概率为 ,红包面值为60元的概率为
,红包面值为60元的概率为 .
.(1)已知小李在该店铺购买了预付款为2000元的商品,且关注了该店铺,求小李实际付款不超过1900元的概率.
(2)若甲、乙两位消费者在该店铺都购买了预付款为2000元的商品,且都关注了该店铺,记甲、乙实际付款分别为
 ,
, 元.令
元.令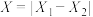 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
您最近一年使用:0次